Лекция 3 (Задачи 2,3,4,6)

Изображение точки на комплексном чертеже Соотношения, возникающие между элементами пространства

1) Совпадение   (А B, точка А совпадает с точкой B);

2) Параллельность  || (a||, прямая a параллельна плоскости );

3) Принадлежность   (А   , точка А принадлежит плоскости  , a);

4 ) Перпендикулярность  (a , прямая a перпендикулярна плоскости );

5) Пересечение   (a   В, прямая a пересекается с плоскостью  в точке В);

6 ) Скрещивание  (a b , прямые a и b скрещиваются);

Центральное и параллельное проецирование

Для отображения элементов пространства (оригиналов) на плоскость используют аппарат центрального и параллельного проецирования.

А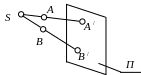 ппарат центрального проецирования:

1) S – центр проецирования;

2) А,В – объекты проецирования,

оригиналы;

3) SA, SВ – проецирующие лучи;

4) П – плоскость проекций;

5) А ^/, B ^/ – проекции точек А и B.

Если центр проецирования удалить в бесконечность, то проецирующие лучи становятся параллельными между собой при этом получают аппарат параллельного проецирования.

Е сли проецирующие лучи параллельного проецирования образуют с плоскостью проекций углы не равные 90°, то такое проецирование называют косоугольным.

α ≠ 90 – косоугольное проецирование;

α = 90 – прямоугольное (ортогональное) проецирование;

α – угол между проецирующими лучами и плоскостью проекций.

Свойства проецирования

1. Проекцией точки на плоскость есть, точка;

2. Проекцией прямой в общем случае является прямая (в частном случае точка);

3. Проекцией плоской фигуры в общем случае есть множество проекций всех её точек; в общем случае это плоская фигура в частном случае отрезок;

4. Если прямая параллельна плоскости проекций, то её проекция параллельна заданной прямой;

5. При параллельном проецировании отношение длин отрезков на прямой и на их проекциях сохраняются.

A

C

B

A^/

B^/

C^/

П

О братимость чертежа – это возможность по проекционным изображениям решать различные метрические и позиционные задачи.

При использовании одной плоскости проекции чертеж является, не обратим.

На рисунке видно, что точка С в пространстве не принадлежит отрезку АВ, хотя С ^/ A^/B^/.

Требованием обратимости чертежа удовлетворяет способ изображения геометрических объектов при использовании прямоугольного проецирования на две и более взаимно-перпендикулярных плоскостей проекций.

Проецирование точки на три плоскости проекций

П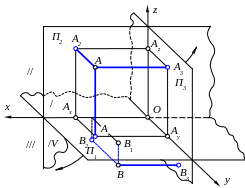 усть в пространстве заданы три взаимно-перпендикулярные плоскости П₁, П₂ и П₃.

П₁ – горизонтальная плоскость проекций,

П₂ – фронтальная плоскость проекций,

П₃ – профильная плоскость проекций,

(•) А – объект проецирования,

АА₁ – горизонтальный луч проецирования,

АА₂ – фронтальный луч проецирования,

АА₃ – профильный луч проецирования,

А₁ – горизонтальная проекция (•) А,

А₂ – фронтальная проекция (•) А,

А₃ – профильная проекция (•) А.

Линии пересечения плоскостей проекций П₁ ∩ П₂ – Ox, П₂ ∩ П₃ – Oz, П₁ ∩ П₃ – Oy – определяют оси прямоугольной системы координат.

Ox, Oy, Oz – называются осями координат.

Координаты точек

Это расстояние точки А (объект проецирования) до плоскостей проекций.

x – широта АА₃ = ОА_х расстояние от точки А до П₃;

y – глубина АА₂ = А₁А_х расстояние от точки А до П₂;

z – высота АА₁ = А₂А_х расстояние от точки А до П₁;

Точка может располагаться в различных четвертях или октантах.

I окт. (y>0, z>0 x>0); II окт. (y<0, z>0, x>0); III окт. (y<0, z<0 , x>0);

IV окт. (y>0, z<0, x>0)

Комплексный чертеж – это чертеж, полученный в результате совмещения плоскостей проекций.

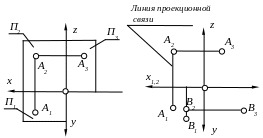
точка А принадлежит первому октанту;

точка В принадлежит /V

четверти.

Для получения комплексного чертежа необходимо:

1. Удалить точку А с отрезками проецирующих лучей АА₁, АА₂ и АА₃;

2. Трехгранный угол, образованный плоскостями проекций П₁, П₂ и П₃ разрезаем по оси y.

3. Совмещаем горизонтальную плоскость П₁, вращением вокруг оси х, до совмещения с плоскостью П₂.

4. Профильную плоскость проекций П₃, вращаем вокруг оси z до, совмещения с плоскостью П₂.

Л инии, соединяющие две проекции одной точки на комплексном чертеже, называются линиями проекционной связи.

А₁А₂ – вертикальная линия проекционной связи Ox.

А ₂А₃ – горизонтальная линия проекционной связи Oz.