
VI.3. Операции над многочленами
В этом разделе
каждый многочлен
![]() ,
представляется массивом коэффициентов
,
представляется массивом коэффициентов
![]() и степенью
и степенью
![]() .
Размер (длина) массива
.
Размер (длина) массива
![]() выбирается с некоторым запасом (т.е.
выбирается с некоторым запасом (т.е.
![]() ).
(Это объясняется тем, что при выполнении
тех или иных операций над многочленами
степень многочлена-результата может
отличаться от степеней многочленов-аргументов.
Так, перемножая многочлены степеней
и
).
(Это объясняется тем, что при выполнении
тех или иных операций над многочленами
степень многочлена-результата может
отличаться от степеней многочленов-аргументов.
Так, перемножая многочлены степеней
и
![]() ,
мы получаем многочлен степени
,
мы получаем многочлен степени
![]() и т.п.) Неиспользуемый "хвост"
массива
при необходимости обнуляют, т.е. полагают
и т.п.) Неиспользуемый "хвост"
массива
при необходимости обнуляют, т.е. полагают
![]() для
для
![]() .
.
63. (Табулирование
многочлена.) Вычислить значения многочлена
![]() в точках
в точках
![]() .
.
Указание.
Вычисление
![]() провести по схеме Горнера:
провести по схеме Горнера:
![]() .
.
Замечание.
Схема Горнера примечательна тем, что
она использует наименьшее число
арифметических операций, необходимых
для вычисления значения многочлена в
заданной точке. Для произвольного
многочлена
![]() степени
требуется
умножений и
сложений-вычитаний. (Для многочленов
частного вида число операций
степени
требуется
умножений и
сложений-вычитаний. (Для многочленов
частного вида число операций
![]() может быть, конечно, уменьшено; см. задачу
III.1.4.)
может быть, конечно, уменьшено; см. задачу
III.1.4.)
64. (Целые корни
целочисленного многочлена.) Дан многочлен
![]() с целыми коэффициентами. Найти целые
корни этого многочлена.
с целыми коэффициентами. Найти целые
корни этого многочлена.
Указание:
если l
– целый корень P(x),
то
![]() делится на l.
делится на l.
65. (Рациональные
корни целочисленного многочлена.) Дан
многочлен
![]() с целыми коэффициентами. Найти рациональные
корни этого многочлена.
с целыми коэффициентами. Найти рациональные
корни этого многочлена.
Указание. Напомним, что рациональное число – это число, представимое в виде отношения целых чисел. Для получения всех рациональных корней (как целых, так и дробных) многочлена Q(x) нужно найти все целые корни многочлена
![]() ,
,
а затем разделить их на q0 (см. задачу 64).
66. (Операции над многочленами от одной переменной.) Даны многочлены Q(x) и P(x). Вычислить:
 – произведение
P(x)
на скаляр c;
– произведение
P(x)
на скаляр c;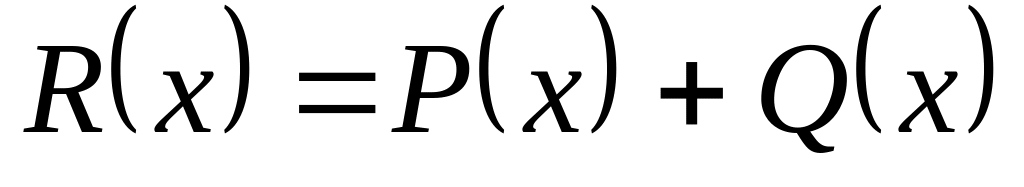 – сумму P(x)
и Q(x);
– сумму P(x)
и Q(x);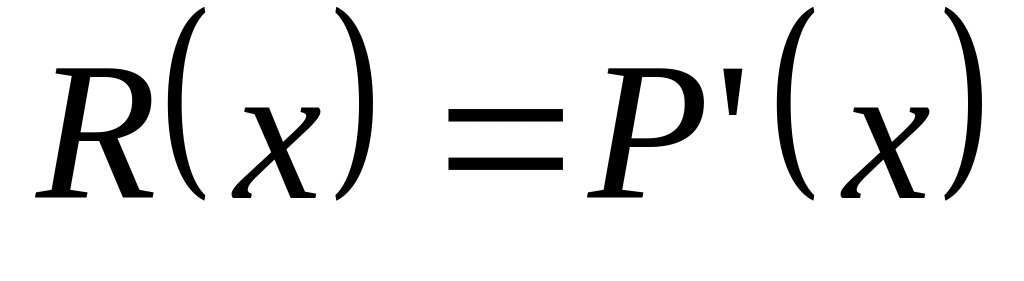 – формальную
производную от P(x);
– формальную
производную от P(x);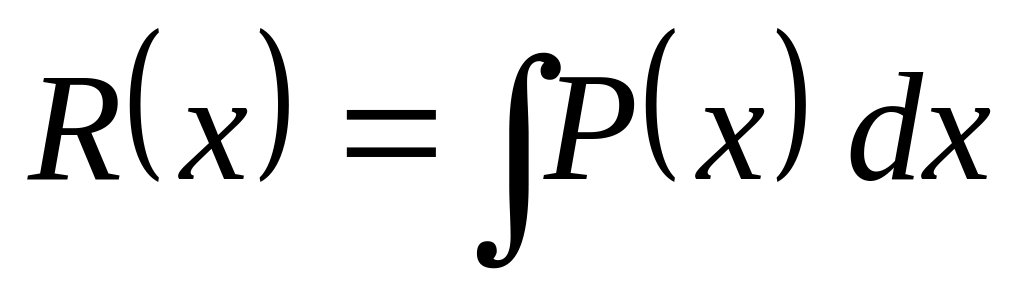 – неопределенный
интеграл от P(x);
– неопределенный
интеграл от P(x);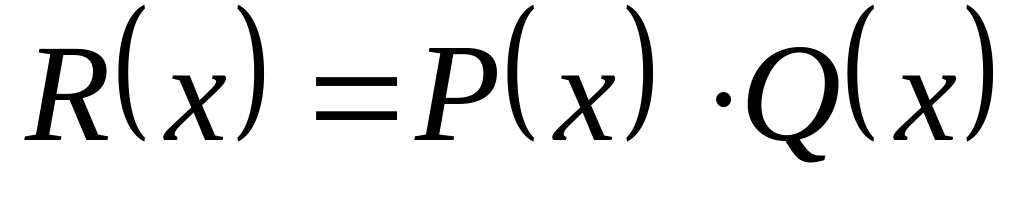 –
произведение P(x)
и Q(x);
–
произведение P(x)
и Q(x);R(x) и S(x) – частное и остаток от деления P(x) на Q(x);
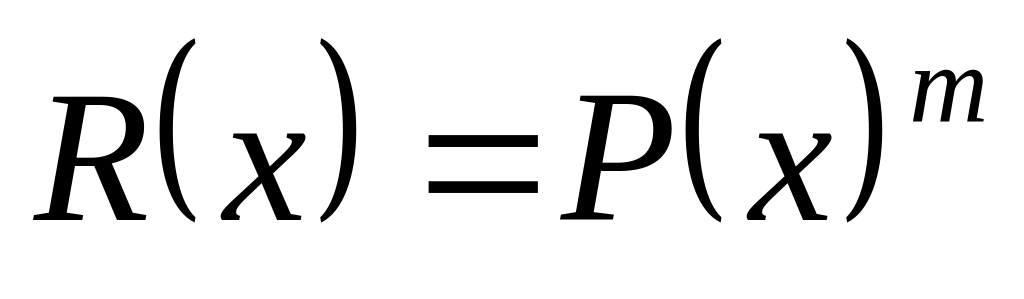 – m-ую
степень P(x);
– m-ую
степень P(x); – многочлен,
получающийся в результате подстановки
Q(x)
в P(x),
раскрытия скобок и приведения подобных
членов.
– многочлен,
получающийся в результате подстановки
Q(x)
в P(x),
раскрытия скобок и приведения подобных
членов.
67. (Бином Ньютона.)
Вычислить коэффициенты многочлена
![]() ,
равного
,
равного
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() .
.
Указание.
 ,
,
 ;
;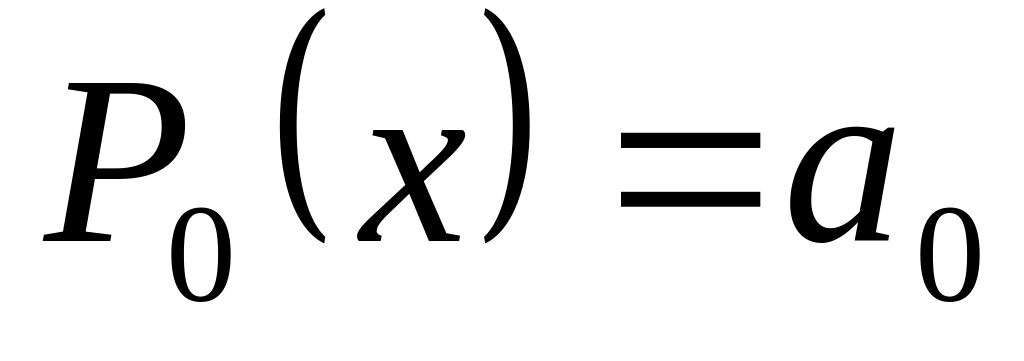 ,
,
 ;
;,
 ,
,

68. (Операции над тригонометрическими многочленами.) Решить задачу 66 для тригонометрических многочленов. (Пункты е) и з) здесь исключаются.)
Указание.
Тригонометрический многочлен степени
m
имеет вид
![]() и задается здесь значением m
и двумя массивами коэффициентов
и задается здесь значением m
и двумя массивами коэффициентов
![]() и
и
![]() .
Как и для степенных многочленов, размер
(длина n)
массивов A
и B
выбираются с некоторым запасом (т.е.
n>m).
Напомним формулы, которые будут здесь
полезны:
.
Как и для степенных многочленов, размер
(длина n)
массивов A
и B
выбираются с некоторым запасом (т.е.
n>m).
Напомним формулы, которые будут здесь
полезны:
![]() ,
,
![]() ,
,
![]() .
.
69. (Формулы Ньютона.) Многочлен
![]() (*)
(*)
представлен набором
чисел
![]() .
Вычислить значения коэффициентов
.
Вычислить значения коэффициентов
![]() многочлена
многочлена
![]() . (**)
. (**)
Другими словами, требуется перейти от формы (*) к форме (**).
Указание.
Отметим, что
![]() ;
;
![]() ,
,
![]() ,
где
,
где
![]() – элементарные симметрические многочлены
от
– элементарные симметрические многочлены
от
![]() ,
определяемые так:
,
определяемые так:
![]()
![]()
![]()
![]()
![]() .
.
Для вычисления
![]() сначала следует вычислить степенные
суммы
сначала следует вычислить степенные
суммы
![]() для k=1,2,…,n,
а затем использовать формулы Ньютона,
связывающие
с суммами Sk:
для k=1,2,…,n,
а затем использовать формулы Ньютона,
связывающие
с суммами Sk:
![]() ,
,
![]() .
.
Предлагаемый здесь
способ вычисления коэффициентов
![]() не является, конечно, обязательным (и
лучшим). Можно, например, просто
последовательно перемножить многочлены
не является, конечно, обязательным (и
лучшим). Можно, например, просто
последовательно перемножить многочлены
![]() по схеме:
по схеме:
![]() ;
;
![]() ,
;
,
;
![]() .
.
70. (Многочлены
Лежандра.) Многочлены
![]() определяются так:
определяются так:
![]() ,
,
![]() ;
;
![]() ,
,
![]()
Вычислить значение многочлена в точке x=a.
В той же точке вычислить значение многочлена
![]() .
.
Многочлен имеет степень n. Вычислить его коэффициенты.
Вычислить коэффициенты
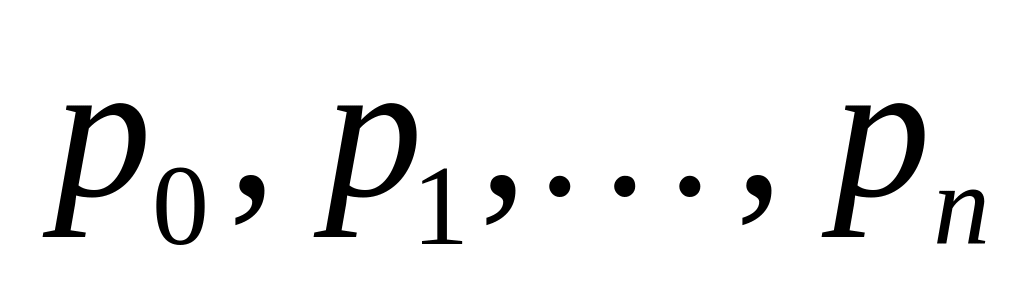 многочлена
многочлена
![]() .
.
71. (Многочлены Бернштейна.) Многочлены
![]()
введены С.Н.Бернштейном
в 1912 году. Они интересны, в частности,
тем, что последовательность
![]() сходится к f(x)
равномерно на отрезке
сходится к f(x)
равномерно на отрезке
![]() ,
если функция f(x)
на этом отрезке непрерывна.
,
если функция f(x)
на этом отрезке непрерывна.
По заданным
значениям
![]() ,
k=0,1,…,n,
вычислить коэффициенты многочлена
,
k=0,1,…,n,
вычислить коэффициенты многочлена
![]() .
.
72. (Интерполяционная формула Лагранжа.) Вычислить коэффициенты p0, p1,…, pn многочлена P(x)=p0+p1x1+…+pnxn такого, что P(ci)=bi, i=0,1,…,n.
Указание:
![]() .
.
73. (Многочлен в форме Ньютона.) Многочлен
P(x)=p0+p1x1+…+pmxm (*)
может быть записан в ньютоновой форме
![]() , (**)
, (**)
где c0,c1,…,cm–1 – некоторые заданные числа.
Вычислить значения многочлена (**) в точке x=a.
Перейти от формы (*) к (**), строя массив u=(u0,u1,…,um) по массивам p=(p0,p1,…,pm) и c=(c0,c1,…,cm–1).
Перейти от формы (**) к форме (*), строя массив p по массивам u и c.
74. (Раскрытие скобок в бесконечном произведении.) Пусть
![]() ,
,
где m
– заданное натуральное число. Раскрывая
скобки, мы можем записать
![]() в виде степенного ряда
в виде степенного ряда
![]() .
.
Вычислить первые
k
его коэффициентов, т.е.
![]() .
.
Замечание. О функции см., например, статью Д.Фукса "О раскрытии скобок, об Эйлере, Гауссе, Макдональде и об упущенных возможностях" в журнале "Квант", №8 за 1981 год, сс. 12-20.
75. (Преобразование Мак-Вильямс.) Многочлен с вещественными коэффициентами от двух переменных
![]()
представлен матрицей
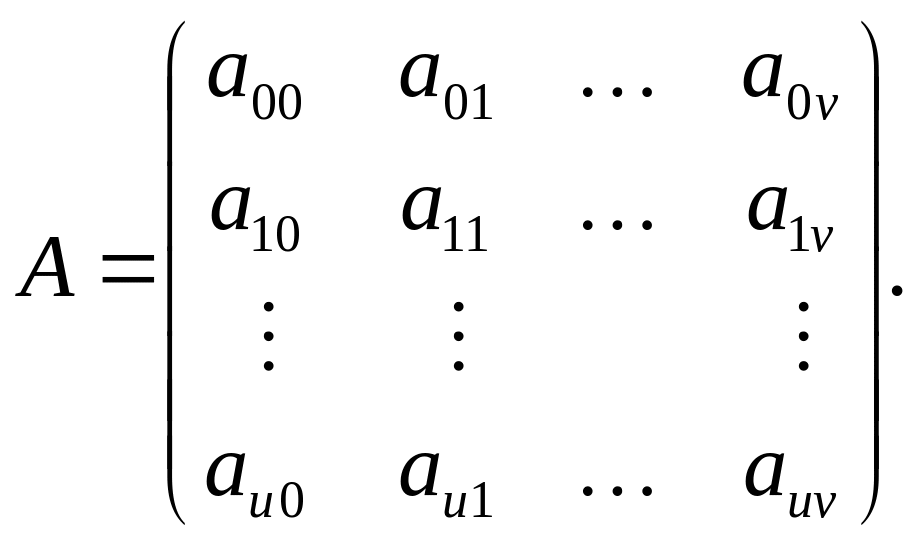
Построить матрицу B=(bmn), представляющую многочлен
![]()
где
![]() .
.
Замечание. Преобразование P(x,y)→Q(x,y) находит применение в алгебраической теории кодирования.
76. (Н.О.Д.)
Найти наибольший общий делитель двух многочленов с целыми коэффициентами.
Найти наибольший общий делитель двух многочленов с рациональными коэффициентами.
Указания.
а) Наибольший общий делитель является
здесь многочленом с целыми коэффициентами.
Использовать алгоритм Евклида. Полезно
предварительно ознакомиться с разделом
4.6.1 книги Д. Кнута "Искусство
программирования для ЭВМ", том 2. –
М.: Мир, 1977. б) Поскольку рациональное
число P
есть отношение a/b
двух целых чисел a
и b,
то каждый многочлен
![]() с рациональными коэффициентами задается
двумя целочисленными массивами
с рациональными коэффициентами задается
двумя целочисленными массивами
![]() и
и
![]() такими, что
такими, что
![]()
![]() .
.
