Практикум на эвм казань ‑ 2007

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Факультет вычислительной математики и кибернетики

Кафедра теоретической кибернетики

Практикум на эвм

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАЧИ

ДЛЯ ПРОГРАММИРОВАНИЯ ПО ТЕМЕ:

«ЦИКЛИЧЕСКАЯ СТРУКТУРА УПРАВЛЕНИЯ. МАССИВ КАК СТРУКТУРА ДАННЫХ»

№2

К азань – 2007

Печатается по решению

кафедры теоретической кибернетики

Казанского государственного университета

Протокол № 5 от 12 апреля 2007 года

Кугураков В.С., Самитов Р.К., Кугуракова В.В.

Практикум на ЭВМ. Задачи для программирования по теме: «Циклическая структура управления. Массив как структура данных». – Казань: КГУ, 2007. – 38 с.

Пособие предназначено для студентов, обучающихся по специальности «Прикладная математика и информатика» и направлению «Информационные технологии», а также для преподавателей, ведущих практические занятия по информатике, алгоритмическим языкам и программированию. Учебный материал представлен задачами для программирования, которые рекомендуется использовать при изучении темы «Циклическая структура управления. Массив как структура данных».

 Казанский государственный университет, 2007

 Кугураков В.С., Самитов Р.К., Кугуракова В.В., 2007

VI. Циклическая структура управления. Массив как структура данных

Инструментальные средства программирования, используемые в разделе:

1. Разнообразные операторы (присваивания, составной, условные, цикла, ввода-вывода).

2. Простые переменные. Одномерные и двумерные массивы с целыми и вещественными компонентами.

3. Оформление программ с использованием определений меток, констант и типов и описаний простых переменных и переменных-массив (применительно к языку программирования Паскаль).

VI.1. Операции над векторами и последовательностями

1. (Скалярное произведение. Модуль вектора.)

   1. Вычислить скалярное произведение векторов и .

   2. Вычислить косинус угла 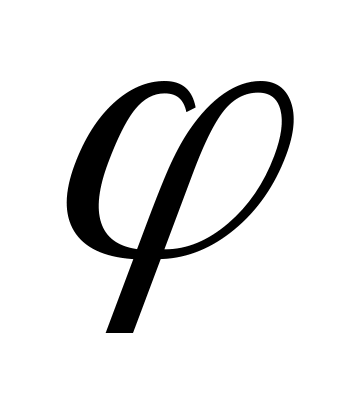между векторами и по формуле , где 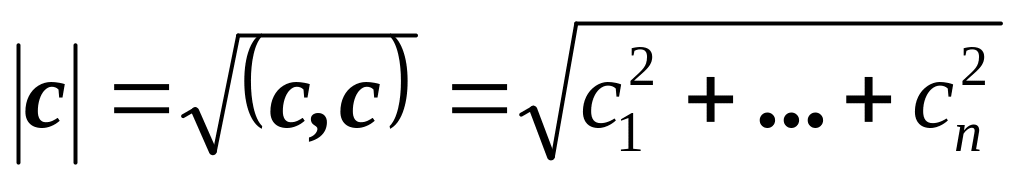– модуль вектора .

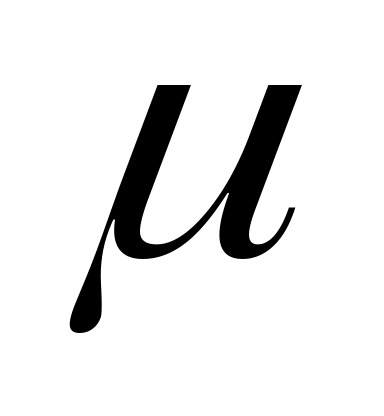2. (Из математической статистики.) Для случайной выборки вычислить: – выборочное среднее; – выборочную дисперсию; , и – выборочные центральные моменты порядков r=2,3 и 4; и – характеристики асимметрии и эксцесса – по формулам:

, ,

, , .

3. (Гармоническое среднее.) Для вектора вычислить гармоническое среднее его компонент

.

Положить S=0, если при вычислении возникает деление на нуль.

4. (Минимальные и максимальные компоненты вектора.) Даны (целочисленный или вещественный) вектор и натуральные числа k, l, m, причем k<n и l m n. Вычислить:

   1. значения минимальной и максимальной компонент в подвекторе ( );

   2. значение индекса максимальной компоненты в подвекторе , причем если несколько компонент имеют максимальное значение, то вычислить значения индекса первой и последней из этих компонент;

   3. число компонент в с минимальным значением;

   4. значение индекса предпоследней компоненты среди компонент вектора , принимающих минимальное значение. (Здесь предполагается, что имеется не менее двух компонент с минимальным значением.)

Указание. Разрешается только однократный просмотр вектора (например, слева на право).

5. (Построение векторов.) Построить векторы , и с компонентами

, , .

(Отметим, что при k→∞.)

6. (Построение векторов знакоперемен и нарушения упорядоченности.) По заданному (целочисленному или вещественному) вектору построить целочисленные векторы и с компонентами

	если < 0,			если ,
	в противном случае;			в противном случае.

7. (Табулирование функции – это процесс получения таблицы значений функции в заданных точках.). Вычислить значения функции y=f(x) в заданных точках . Результаты напечатать в виде таблицы.

Варианты задания:

а)	;
б)	если , , в остальных случаях;
в)	если , если ,

где символ означает суммирование по тем , для которых и ( и – заданные числа).

8. (Операции над множествами.) Дано некоторое множество из m элементов. Каждое его подмножество Т может быть представлено своим характеристическим вектором 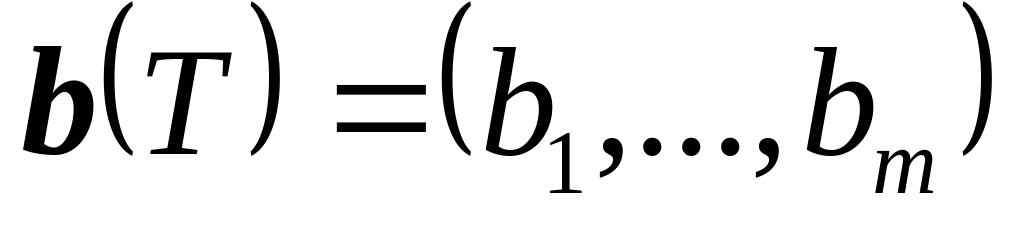, где

	если ,
	если .

Подмножеству Т сопоставляется номер (Отметим, что и , где  – пустое множество.)

Пусть T₁ и T₂ – подмножества в S, представленные характеристическими векторами b(T₁) и b(T₂).

1. Вычислить card (T₁) – число элементов в T₁.

2. Установить истинность включения .

3. Построить векторы b(T) для

.

4. Вычислить n(T₁) – номер подмножества T₁.

5. По номеру подмножества T₁ построить вектор b(T₁).

9. (Десятичное представление натурального числа.) Для заданного натурального числа n (n<10⁹) построить вектор c=(c₁,…,c₉), где c_s – s‑ая цифра (литера) в десятичной записи числа n. (Младшие разряды – справа. Таким образом, n=c₁10⁸+c₂10⁷+…+c₉.)

10. (Построение вектора.) По заданному вещественному вектору x=(x₁,…,x_n) построить вектор y=(y₁,…,y_n), компоненты которого определяются по формуле

, s=1,2,…,n.

11. (Преобразование векторов.)

    1. Записать вектор x=(x₁,…,x_n) в обратном порядке. (Другими словами, построить вектор y=(x_n,x_n–1,…,x₁).)

    2. Осуществить циклический сдвиг вектора x=(x₁,…,x_n) влево и вправо на одну позицию. (Другими словами, построить векторы y=(x₂,…,x_n,x₁) и z=(x_n,x₁,…,x_n–1).)

    3. Для вектора x=(x₀,…,x₃₂) построить вектор

y=(x₁, x₂, x₀, x₄, x₅, x₃, x₇, x₈,x₆,…, x₃₁, x₃₂, x₃₀).

4. Для вектора x=(x₁, x₂,…,x_2n) построить вектор

y=(x_2n, x₃, x₂, x₅, x₄, x₇,x₆,…, x_2n–1, x_2n-2, x₁).

(Другими словами, компоненты с четными индексами циклически сдвигаются вправо, а с нечетными – влево.)

5. Для векторов x=(x₀,…,x_n–1) и y=(y₀,…,y_n–1) построить вектор z=(z₀,…,z_3n–1), где

, , , k=0,1,…,n–1.

12. (Цепные дроби.) Вычислить:

а) y=[a₁; b_n–1, a₂; b_n–2, a₃; …; b₁, a_n];

б) y=[xⁿ; a₁n!, x^n–1; a₂(n­–1)!, x^n–2; …; a_n–12!, x¹; a_n1!, x⁰],

где [s₀; r₁, s₁; r₂, s₂; …; r_n, s_n] обозначает “многоэтажную” цепную дробь

.

13. (Обработка упорядоченной последовательности.) Дана последовательность x=(x₁,…,x_n) натуральных чисел, упорядоченных по неубыванию, т.е. x₁  x₂ … x_n. Элемент последовательности x назовем одиночкой, если его значение отлично от значения любого другого элемента в x. Группу элементов x_m+1, x_m+2, …, x_m+k назовем цепочкой длины k (k1), если x_m < x_m+1=x_m+2=…=x_m+k < x_m+k+1.

1. Вычислить s – количество цепочек в x.

2. Построить вектор y=(y₁,…,y_n), где

3. Построить вектор v=(v₁,…,v_n), где v_i – количество цепочек в x длины i.

4. Построить вектор u=(u₁,…,u_n), где u_i – длина i-ой цепочки. (Если в x содержится k<n цепочек, то положить u_i=0 для i>k.)

5. Построить векторы a=(a₁,…,a_n) и b=(b₁,…,b_n), где a_i и b_i – индексы первого и последнего элементов в i-ой цепочке. (Если в x содержится k<n цепочек, то положить a_i=b_i=0 для i>k.)

6. Вычислить t – количество одиночек в x.

7. Построить вектор w=(w₁,…,w_n), где

8. Построить вектор z=(z₁,…,z_n), где

Пример. Пусть x=(1, 2,2,2, 3,3, 4, 5, 6,6, 8). Тогда а) s=7; б) y=(1,2,0,0,3,0,4,5,6,0,8); в) u=(1,3,2,1,1,2,1,0,0,0,0); г) v=(4,2,1,0,0,…,0); д) a=(1,2,5,7,8,9,11,0,…,0), b=(1,4,6,7,8,10,11,0,…,0); е) t=4; ж) w=(1,0,0,0,0,0,4,5,0,0,8); з) z=(0,2,0,0,3,0,0,0,6,0,0).

14. (Массивы переменной длины, или три вариации на тему задачи 13.) Дана последовательность x=(x₁,…,x_n) натуральных чисел, упорядоченных по неубыванию, т.е. x₁  x₂ … x_n.

1. Образовать новую последовательность x', включая в нее по одному элементу каждой цепочки из x.

2. Образовать новую последовательность x'', исключая из x одиночки.

3. Образовать новую последовательность x''', исключая из x цепочки длины ≥2 (то есть, включая в x''' только одиночки).

Пример. Для x=(1, 4,4, 6,6,6, 9) имеем: а) x'=(1,4,6,9); б) x''=(4,6); в) x'''=(1,9). Если в используемом языке программирования отсутствует массивы переменной длины, то следует получить такие последовательности: а) x'=(1,4,6,9,0,0,0); б) x''=(4,6,0,0,0,0,0); в) x'''=(1,9,0,0,0,0,0), заполняя свободные "хвосты" последовательностей нулями.

15. (Неубывающие цепочки.) Дана последовательность x=(x₁,…,x_n) натуральных чисел. Ее подпоследовательность (x_m+1, x_m+2,…, x_m+k) назовем неубывающей цепочкой длины k, если x_m+1 x_m+2 … x_m+k, но x_m > x_m+1 и x_m+k > x_m+k+1.

1. Вычислить s – длину самой короткой и t – длину самой длиной из неубывающих цепочек в x.

2. Построить вектор u=(u₁,…,u_n), где u_k – число неубывающих цепочек в x длины k.

3. Построить векторы v=(v₁,…,v_n), w=(w₁,…,w_n), где v_i и w_i – индексы 1-го и последнего элементов в i-ой цепочке последовательности x. (Если в x содержится l<n цепочек, то положить v_i=w_i=0 для i>l.)

Пример. Пусть x=(1,2,3,8, 4, 3,5, 4, 3, 1,7, 2). Тогда а) s=1, t=4; б) u=(4,2,0,1,0,…,0); в) v=(1,5,6,8,9,10,12,0,…,0), w=(4,5,7,8,9,11,12,0,…,0).

16. (Тригонометрическое интерполирование.) Даны m значений y_k=y(x_k) функции y(x) в точках x_k=kT/m, k=0,1,…,m–1. Требуется аппроксимировать y(x) на интервале (0,T) тригонометрическим полиномом

, ,

так, чтобы минимизировать величину – сумму квадратов отклонений. Известно, что коэффициенты A_i и B_i, удовлетворяющие этим требованиям, определяются по формулам

, , .

Вычислить коэффициенты A_i, B_i аппроксимирующего тригонометрического полинома.

17. (Треугольник Паскаля.) Построить вектор c=(c₀,c₁,…,c_n), где – число сочетаний из n элементов по i.

Указание: для i=1,2,…,n–1; .

18. (Н.О.Д.) Вычислить d_n=Н.О.Д.(u₁,u₂,...,u_n).

Указание: d₁=u₁; d_n=Н.О.Д.(d_n–1,u_n), n ≥ 2 (см. задачу I.1.8).

19. (Число способов образования бинарного, но не ассоциативного произведения n сомножителей.) Последовательность чисел a₁, a₂,… определена рекуррентно:

a₁=1;

a_n=a₁a_n–1+a₂a_n–2+…+a_n–1a₁, n ≥ 2.

1. Построить вектор (a₁, a₂, …, a₁₆).

2. Проверить для k=1,2,…,16, что .

Примечание. Числа a_k, называемые числами Каталана, имеют следующий комбинаторный смысл: a_k равно числу возможных способов расстановки скобок в произведении x₁x₂…x_n. Например, для k=4 возможны лишь такие расстановки: ((x₁x₂)x₃)x₄, (x₁x₂)(x₃x₄), (x₁(x₂x₂))x₄, x₁((x₂x₃)x₄), x₁(x₂(x₃x₄)), т.е. a_k=5.

20. (Табулирование функции, представленной рядом.) Вычислить значения функции f(x) в заданных точках x=(x₁,…,x_n). В качестве f(x) взять одну из функций:

1. ;

2. ;

3. ;

4. .

Варианты задания:

1. при вычислении бесконечной суммы суммирование прекратить, как только очередной член ряда становится по абсолютной величине ≤ε (здесь ε>0 – заданное число);

2. в бесконечной сумме учесть только первые m слагаемых (здесь m – заданное натуральное число).

Замечание. Пусть k – любое из чисел 1, 2, 3 или 4, f=f_k, а f*(x) – вычисленное значение функции f в точке x. Из теории известно, что если 0≤x<1, то f(x)=(arcsin x)^k, и, следовательно, . Поскольку f*(x) есть приближенное значение для f(x), то, вообще говоря, f*(x)f(x) и . Полезно вычислить значения величин:

,

для x_i=0.05, 0.10, 0.15, …, 0.95 и по их отклонению от 0 судить о том, насколько точно величины f*(x_i) оценивают f(x_i).

21. (Поиск приближенных формул.) Авторы где-то читали (но забыли, где конкретно), что где f_k(x) обозначает сумму

.

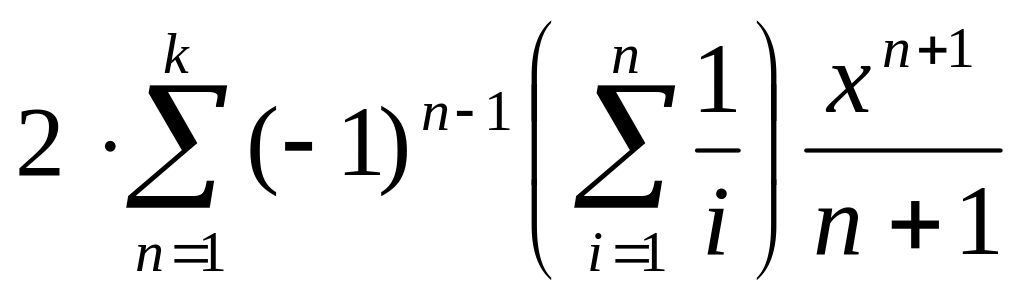1. Подобрать для каждого x_m=0.01m, m=1, 2, …, 99, такое наименьшее натуральное число k_m, что

, (_*)

где >0 – заданное число.

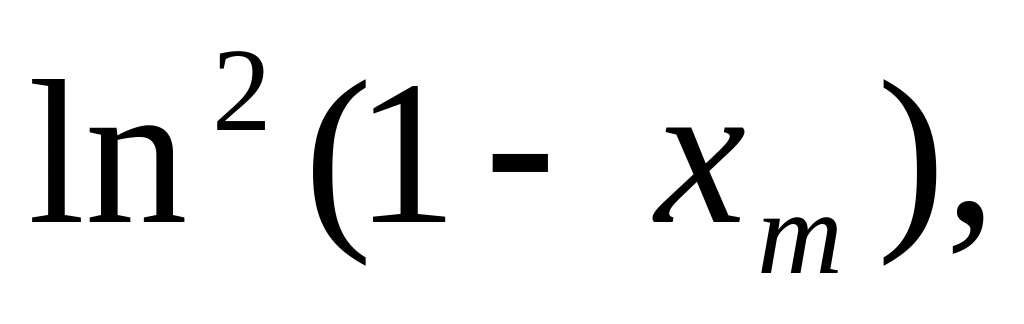
2. Напечатать таблицу значений x_m, k_m, для m= –99, –98,…, –1, 1, 2,…,99.

3. Вычислить коэффициенты a₂, a₃, …, a_k+1 многочлена a(x)=a₂x²+a₃x³+…+a_k+1x^k+1 такого, что a(x)=f_k(x), где k – максимальное из чисел k_–99,…,k_–1, k₁,…,k₉₉.

Замечание. В результате можно получить приближенную формулу . Чтобы оценить качество этой формулы, проведите соответствующий эксперимент, вычисляя значения и a(x) в нескольких точках, например, для x=0,01m, m=1,2,…,99. Другой вариант задания состоит в замене условия (_*) на

. (_**)

4. Проделать то же самое для соотношения

Указание. Для вычисления натурального логарифма и арктангенса использовать стандартные арифметические функции ln(x) и arctan(x).

22. (Обработка целочисленного вектора.) Дан целочисленный вектор .

1. Вычислить S – сумму положительных (отрицательных) компонент вектора a.

2. Вычислить q – число перемен знака в последовательности компонент вектора a.

3. Установить, упорядочены ли компоненты вектора a по возрастанию или убыванию.

4. Установить, имеются ли у вектора a одинаковые компоненты.

5. Компоненту a_i вектора a назовем уникальной, если ее значение отлично от значения других компонент. Вычислить t – число уникальных компонент вектора a.

6. Вычислить r – число различных значений, которые имеют компоненты вектора a. (Другими словами, если , то компоненты учитываются при подсчете как одна компонента.)

7. Вычислить p – число компонент вектора a, значения которых являются простыми числами.

8. Преобразовать вектор a, помещая отрицательные компоненты в начало вектора, а положительные – в конец. Рассмотреть два варианта алгоритма: (1) используя вспомогательный массив и (2) не используя его.

9. Предположим, что компоненты вектора a упорядочены, а именно: a₁≤a₂≤…≤a_n. Для заданного целого числа m установить, существует ли индексы i и k такие, что 1≤i≤k≤n и a_i+a_i+1+…+a_k=m.

10. Вычислить l – число компонент вектора a, взаимно простых с заданным числом k.

23. (Вектор попаданий в интервалы.) Дан вещественный вектор . Построить вектор s=(s₁,…,s_t), где s_j равно числу компонент вектора x, принадлежащих интервалу [a+(j–1)h, a+jh), j=1,…,t. Рассмотреть следующие варианты задания:

1. a (левая граница первого интервала) и h (длина интервала) заранее заданы;

2. считать, что компоненты вектора x упорядочены по неубыванию, т. е. x₁≤x₂≤…≤x_n; положить , a=x₁, b=x_n.

24. (Числа Фибоначчи.) Числа Фибоначчи F_n определяются так: F₀=0, F₁=1; F_n=F_n–1+F_n–2 для n=2,3,…

Проверить следующие свойства чисел Фибоначчи для m, n≤30:

1. если m=2n+1, то F_m=1+F₂+F₄+…+F_2n;

2. если m=2n+2, то F_m=F₁+F₃+F₅+…+F_2n+1;

3. если m=3n, то ;

4. если m=n+k, то F_m=F_n–1F_k+F_nF_k–1 (1≤k, n≤m–1);

5. если m делится на n; то F_m делится на F_n;

6. если m=2n+1 или 2n+2, то

7. н.о.д.(F_n, F_n+1)=1.

Указание: построить предварительно массив (F₀, F₁,…,F₃₀).

25. (Фибоначчиeва система счисления.) Известно, что каждое целое число n ≥ 1 можно однозначно представить в виде

_, (_*)

где F_m – m-ое число Фибоначчи (см. задачу 24), k_r ≥ 2, k_i–1 ≥ k_i+2. Получить разложение (*) для произвольного n ≤ 1000000.

Указание. Имеется 31 число Фибоначчи, не превосходящих 1000000. Для получения разложения (_*) требуется построить двоичный вектор (x₀,x₁,…,x₃₀), у которого все компоненты нулевые, кроме компонент (с индексами k₁,…,k_r), которые равны 1. При этом индекс k₁ равен наибольшему k, для которого n≥F_k, k₂ равен наибольшему k, для которого и т.д.

26. (Логарифмически вогнутая последовательность.) Последовательность вещественных чисел a=(a₁,…,a_n) называется логарифмически вогнутой, если для k=2,3,…,n–1. Для заданной последовательности

1. установить, является ли она логарифмически вогнутой;

2. найти наибольшее m (m≤n), при котором подпоследовательность (a₁,…,a_m) логарифмически вогнута;

3. найти наибольшее m, для которого существует r такое, что подпоследовательность (a_r+1,a_r+2,…,a_r+m) логарифмически вогнута (здесь 0≤r≤n–m).

27. (Разреженные векторы.) Вещественный вектор a=(a₁,…,a_n), большинство компонент которого равно нулю, назовем разреженным вектором. (Понятие "большинство" здесь никак не определяется и требует уточнения.) Такой вектор иногда удобно представлять в уплотненном виде парой <b,m>, где b и m — векторы, в которых перечислены в одинаковом порядке соответственно ненулевые компоненты и номера (индексы) ненулевых компонент вектора a. (Например, если a=(0,1,10,5,0,0,4,0), то b=(1,10,5,4) и m=(2,3,4,7).)

1. Построить уплотненное представление <b,m> разреженного вектора a.

2. Выполнить обратное преобразование от <b,m> к a.

3. Найти значение a_i (i-ой компоненты вектора a) по заданной тройке <i,b,m>.

4. Вычислить скалярное произведение двух векторов, представленных в уплотненном виде.

28. (Слияние упорядоченных последовательностей.) Слить две упорядоченные последовательности x=(x₁,…x_m) и y=(y₁,…y_n) такие, что x₁≤x₂≤…≤x_m и y₁≤y₂≤…≤y_n, в одну упорядоченную последовательность z=(z₁,…z_n+m) так, чтобы z₁≤z₂≤…≤z_m+n. (Например, для x=(0,0,1,1,5,6,6) и y=(0,1,3,3,7) должны получить z=(0,0,0,1,1,1,3,3,5,6,6,7).)

Указание. Полезно удлинить x и y на один элемент, полагая x_m+1=y_m+1=max{x_m,y_n}. (Почему?)

29. (Логарифмический поиск, или метод деления пополам.) Даны набор чисел такой, что , и число y. Вычислить индекс k, для которого . (Если y или x_n<y, то положить соответственно k=m и k=n+1.)

Указание. Можно последовательно (начиная с ) просмотреть набор x и найти соответствующее k. Однако, здесь это не лучший способ: такой поиск требует в среднем O(n) операций сравнения, в то время как можно предложить более быстрый алгоритмы. Следующий способ вычисления k требует O(log₂n) операций сравнения. Разобьем набор x пополам, на два поднабора и , где s – целая часть от деления n–m+1 на 2. Если y≤x_s, то, очевидно, k≤s; в противном случае k>s. В первом случае, чтобы найти k, нужно провести соответствующий поиск в поднаборе x', а во втором – в поднаборе x''. Деление соответствующих поднаборов продолжается до тех пор, пока не будет получен поднабор из одного числа. Проиллюстрируем это на следующем примере (для y=5):

	1	2	3	4	5	6	7	8	9	10	11	-индексы
x=	1	2	2	3	4	4	6	7	8	9	9	-исходный набор
						4	6	7	8	9	9	-шаг 1
						4	6	7				-шаг 2
							6	7				-шаг 3
							6					-шаг 4
												-искомый индекс k=7

30. (Сортировка по методу "пузырька".) Упорядочить (то есть переставить) элементы числовой последовательности x=(x₁,…,x_n) по неубыванию их значений, используя метод "пузырька".

Указание. Метод "пузырька" основан на следующей идее: "легкие" элементы всплывают, "тяжелые" – оседают на дно. Применительно к x это означает, например, следующее:

Первый алгоритм. В множестве x_i,x_i+1,…,x_n найдем минимальный элемент x_j, а затем поменяем x_i и x_j местами. Эти действия последовательно повторяем для i=1,2,3,…,n–1.

Второй алгоритм. Осуществим просмотр x, сравнивая при этом соседние элементы x_i и x_i+1 для i=1,2,… Каждый раз, когда x_i>x_i+1, элементы x_i и x_i+1 меняем местами. Эти действия повторим для подпоследовательностей . Алгоритм прекращает работу, если при просмотре очередной последовательности ни одна пара соседних элементов не меняется местами.

Дополнительное задание. Оценить временную сложность предложенных алгоритмов.

31. (Алгоритм Дж. фон Неймана.) Метод сортировки последовательности x=(x₁,…,x_n), предложенный в задаче 30, привлекает своей простотой. Однако он требует выполнения O(n²) операций сравнения и перестановки, в то время как существует более быстрые методы. Так, в методе, предложенном американским математиком Дж. фон Нейманом, требуется O(n log₂n) операций. Суть этого метода заключается в следующем:

1. Если n=1, то последовательность x упорядочена.

2. Если , то разобьем x на две части x'=(x₁,…,x_m) и x''=(x_n+1,…,x_n) примерно одинаковой длины (а именно: m=s, если n=2s или 2s+1). Далее упорядочиваем отдельно x' и x'', а затем сливаем их в одну упорядоченную последовательность x (см. задачу 28).

Этот метод иллюстрируется на следующем примере, где цифрами 1,2,3 обозначены шаги алгоритма, на которых сливаются соответствующие подпоследовательности:

5	4	2	7	9	1	8
4	5	2	7	1	9	8
2	4	5	7	1	8	9
1	2	4	5	7	8	9

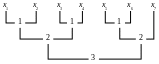
Отметим, что при использовании этого метода возникает необходимость во вспомогательном массиве y такой же длины, что и x, необходимом для слияния подпоследовательностей; иначе число перемещений элементов резко возрастает.

Конкретное задание. Упорядочить последовательность x, используя предложенный алгоритм. Для простоты взять .

32. (Двоичные векторы длины n.) Построить все двоичные векторы длины n. (Например, для n=3 необходимо построить векторы 000,001,010,011,100,101,110,111.)

33. (Обработка изоморфных объектов.) В векторе , компоненты которого суть объекты одного и того же типа (числа, векторы, матрицы и т. д.), могут быть одинаковые компоненты. Из каждой группы тождественных между собой компонент оставить только одну компоненту, вычеркивая остальные, понимая под вычеркиванием компоненты замену ее значения на некоторое "пустое" значение.

34. (Любое натуральное число есть сумма не более, чем девяти кубов.) Найти все решения уравнения в целых числах . Здесь N равно порядковому номеру того года, когда решается эта задача.

Указание. 9-кратный цикл – здесь неприемлемое решение.

35. (Аддитивные цепочки.) Последовательность натуральных чисел называется аддитивной цепочкой для числа m, если

1. a₁=1, a_n=m;

2. a₁<a₂<…<a_n;

3. для любого i=2,3,…,n элемент a_i представим в виде a_i=a_j+a_k при некоторых . (Если при этом j=i–1, то цепочку называют линейной.)

Установить, является ли заданная последовательность аддитивной цепочкой для заданного числа m; если да, то является ли она линейной. (Пример линейной аддитивной цепочки: 1,2,4,8,9,17,18,35.)

36. (Аддитивно-разностные цепочки.) Последовательность натуральных чисел называется аддитивно-разностной цепочкой для числа m, если

1. a₁=1, a_n=m;

2. для любого i=2,3,…,n элемент a_i представим в виде или a_i=a_j+a_k при некоторых j,k<i.

Установить, является ли заданная последовательность аддитивно-разностной цепочкой для заданного числа m.

37. (Аддитивные базисы.) Последовательность неотрицательных целых чисел называется аддитивным базисом для множества , если любое число s представимо в виде s=a_i+a_k для некоторых .

Установить, является ли данная последовательность аддитивным базисом для M_m, где – заданное целое.

38. (Одно преобразование из поточного шифра Panama.) Отображение, заданное на множестве двоичных векторов длины n сопоставляет вектору (a₀,a₁,…,a_n–1) вектор (b₀,b₁,…,b_n–1), компоненты которого определяются как

b_i=(a_i+a_i+1a_i+2+a_i+2+1) mod 2, i=0,1,...,n–1,

где индексы приводятся по модулю n, т.е. , . При четном n это отображение не является взаимно однозначным, поскольку векторы (0,0,…,0) и (0,1,0,1,…,0,1) отображаются в один и тот же вектор (1,1,…,1). При n=3 отображение является взаимно однозначным, в чем, например, можно убедиться, построив соответствующую таблицу:

a0a1a2	000	001	010	011	100	101	110	111
b0b1b2	111	010	100	101	001	110	011	000

Установить, будет ли указанное отображение взаимно однозначным при n=5,7,9,11,13,15,17.