9.5 Контрольні запитання

Лабораторна робота № 10

Дослідження пасивних r-c та l-c фільтруючих ланок

Мета заняття: ознайомитись з практичними схемами пасивних фільтрів різних порядків з R-C та L-C ланками, вивчити їх принципи дії та способи зміни характеристик

Завдання:

1) вивчити практичні схеми пасивних фільтрів різних порядків з R-C та L-C ланками;

2) освоїти способи під’єднання різноманітного навантаження до виходу фільтрів;

3) дослідити роботу пасивних фільтрів з різними видами сигналів;

4) вивчити способи зміни характеристик пасивних фільтрів.

Тривалість роботи: 4 год.

10.1 Основні теоретичні положення

Електричними фільтрами прийнято вважати чотириполюсники, які вмикаються між джерелом живлення змінної напруги і навантаженням. Їхнім призначенням є можливість без затухання пропускати до навантаження струми одних частот і затримувати, або пропускати, але з великим затуханням струми інших частот.

Діапазон частот, що пропускаються фільтром без затухання називається смугою прозорості, а діапазон частот, що пропускаються з затуханням – смугою затухання.

Електричні фільтри з високими крутизнами спаду і наростання виконуються з котушок індуктивності і конденсаторів. У випадку високого опору навантаження, або невисоких значень якісних характеристик використовуються пасивні RC-фільтри.

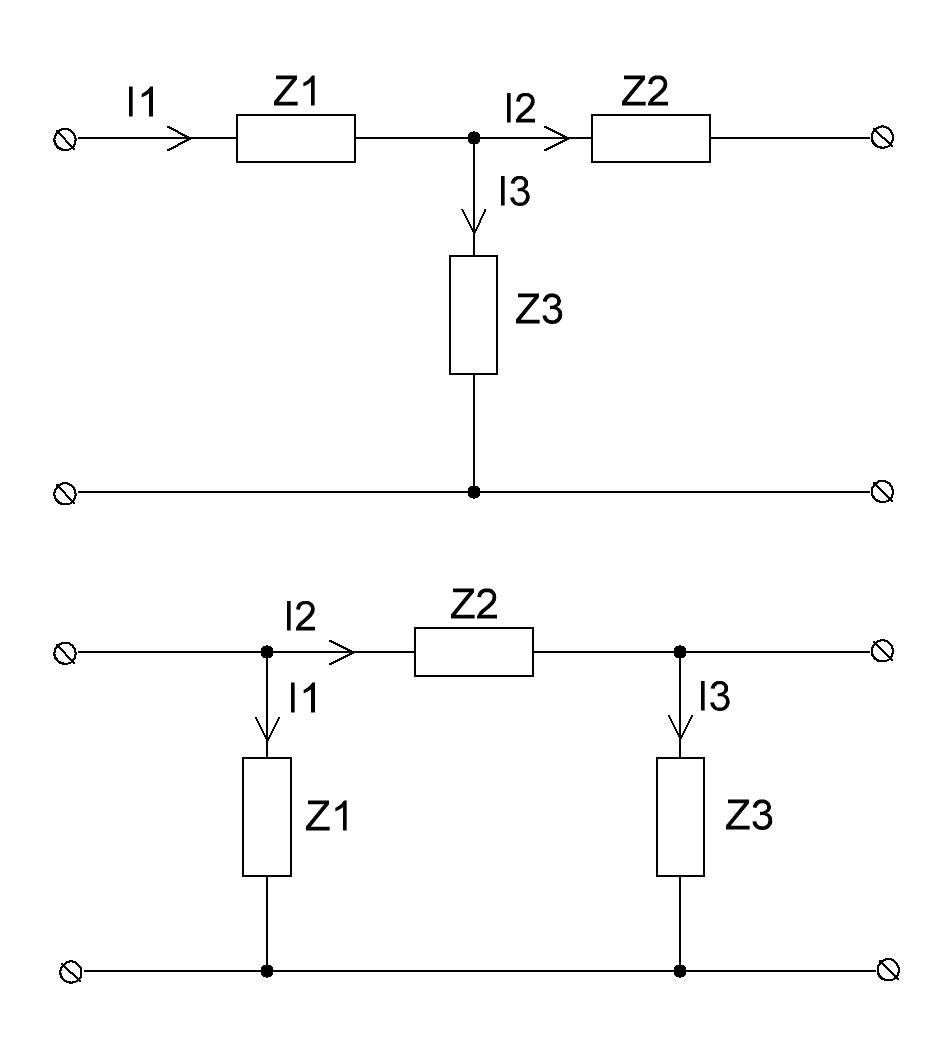
Як правило, фільтри будуються за симетричною Т, або П – подібнми схемами (рис. 10.1). Оскільки при ВЧ індуктивні опори котушок індуктивності є набагато більшими за їх активні опори, будемо вважати, що активні опори котушок і активні провідності конденсаторів рівні нулю, тобто, що фільтри складаються з ідеальних реактивних елементів з опорами Z.

Опори ₁, в схемі на рисунку 10.1, а та в схемі на рисунку 10.1, б прийнято називати поздовжніми, а в схемі на рисунку 10.1, а та в схемі на рисунку 10.1, б – поперечними.

Фільтри, в яких добуток поздовжнього опору на відповідний поперечний опір є постійним для даного фільтру числом (числом ), що не залежить від частоти, називаються -фільтрами.

б

а – Т-подібний, б – П-подібний

Рисунок 10.1 - Структурні схеми пасивних фільтрів.

Фільтри, в яких добуток залежить від частоти, називаються -фільтрами.

Опір навантаження, який вмикається на виході фільтра повинен бути узгоджений з характеристиками опору фільтра. В -фільтрах цей опір суттєво змінюється у залежності від частоти , що знаходиться у смузі прозорості. Це викликає необхідність зміни опору навантаження в функції від частоти.

В -фільтрах при певних значеннях коефіцієнта опір навантаження моло змінюється від частоти (в межах смуги прозорості), а тому навантаження може бути одним і тим самим по величині для різних значень .

Якість фільтра тим вища, чим різкіше зростає затухання у смузі затухання [1].

Для розрахунку параметрів фільтра необхідно знайти опори його ланок за коефіцієнтами чотириполюсника А, В, С, D [1].

Для Т-подібного фільтра вхідну напругу та струм виразимо через вихідні напругу та струм:

(10.1)

(10.2)

Тоді:

(10.3)

(10.4)

(10.5)

(10.6)

Аналогічні викладки для П-подібної схеми матимуть вигляд:

(10.7)

(10.8)

(10.9)

(10.10)

Відомо, що коли навантаження узгоджене з характеристичним опором чотириполюсника, то вихідна напруга і струм на навантаженні пов’язані з напругою і струмом на вході чотириполюсника наступними співвідношеннями:

(10.11)

(10.12)

де

Тоді

(10.13)

(10.14)

Множник визначає, в скільки раз модуль напруги (струму) на виході фільтра менший за модуль напруги (струму) на вході фільтра.

Якщо а=0, то = =1 і фільтр пропускає коливання без затухання. Таким чином, в смузі прозорості а=0.

У смузі затухання a>0. Множник , по модулю рівний нулю, свідчить про те, що напруга і струм відстають відповідно від і на кут b.

Фільтруючі властивості чотириполюсника розглянемо шляхом порівняння виразу для коефіцієнта А чотириполюсника з рівним йому виразом гіперболічного конуса від аргументу a=jb:

(10.15)

Гіперболічний конус від суми двох аргументів (з врахуванням того, що ch jb=cos b і jb=j sin b) можна представити наступним чином:

(10.16)

Для будь-яких фільтрів, зібраних за Т-схемою і П-схемою відношення опорів Z між собою завжди є дійсним числом – бо відношення двох уявних чисел завжди є дійсним числом.

Відповідно завжди буде дійсним коефіцієнт А. Звідси дійсним повинен бути і вираз рівний йому :

(10.17)

Вираз (10.17) дійсний, якщо

(10.18)

При цьому

(10.19)

Рівняння (10.18) і (10.19) використовують для визначення границь смуги прозорості і характеру зміни кута b в зоні прозорості, а також характеру зміни коефіцієнта затухання а в смузі затухання.

Рівність (10.17) для смуги прозорості (а=0) задовільняється, оскільки sha=sh 0=0. В силу того що ch 0=1, рівняння (10.19) для смуги прозорості переходить в наступне:

(10.20)

Круговий конус (cos b) може змінюватися в межах від +1 до -1. Тому крайні значення коефіцієнта А (що є функцією частоти )в смузі прозорості рівні ±1. Смуга прозорості в загальному випадку лежить в діапазоні частот від до . Значення і для фільтрів НЧ і ВЧ визначається шляхом розв’язання наступного рівняння:

(10.21)

Для смугових та загороджуючих фільтрів і знаходять як корені рівняння Для них рівняння дає можливість визначити так звану резонансну частоту , що знаходиться в інте6рвалі між і .

Частоту, що є граничною між смугою прозорості і смугою затухання, називають частотою зрізу.

Характер зміни кута b у функції від для смуги прозорості визначається у відповідності з рівнянням (10.20) наступним чином:

(10.22)

Визначаємо а і b для смуги затухання. В смузі затухання a>0. Рівняння (10.18) задовільняється при умові:

(10.23)

тобто при

b=0 (10.24)

і (або)

b=±π. (10.25)

Згідно з рівнянням (1.19), при b=0:

(10.26)

а при b=±π

(10.27)

Рівняння (10.26) і (10.27) дозволяють за значенням А як функції знайти cha в смузі затухання, а за cha знайти а і, таким чином, побудувати криву . З рівнянь (10.24), (10.25) виходить, що в смузі затухання напруга на виході фільтра знаходиться або в фазі (при b=0), або в протифазі (при b=±π) з напругою на вході фільтра.

При цьому необхідно відмітити, що:

Зі зміною частоти змінюються коефіцієнти В і С чотириполюсника, тому змінюється і характеристичний опір Для того, щоб фільтр працював на узгоджене навантаження, при зміні частоти потрібно змінювати і опір навантаження.

У смузі прозорості характеристичний опір фільтра завжди активний, а в смузі затухання – чисто реактивний (індуктивний або ємнісний).

Розглянемо, як класифікуються фільтри по відношенню до опрацьовуваної смуги частот.

Фільтрами низької частоти (ФНЧ) називають фільтри, що пропускають на навантаження лише низькі частоти: від до . Смуга їх затухання знаходиться на інтервалі від до ∞.

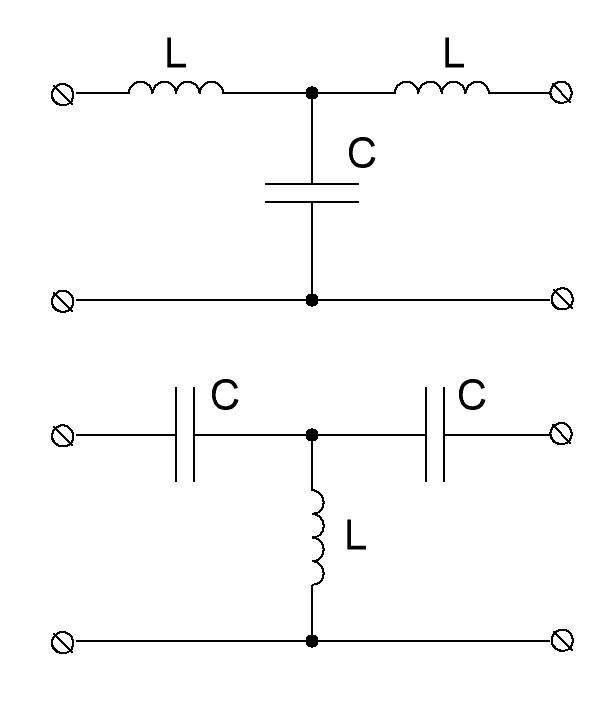
Схеми двох ФНЧ наведені на рис. 10.2, а, б. Характер зміни коефіцієнта затухання а і коефіцієнта фази b якісно зображають криві на рис. 10.2, в.

Під фільтрами високої частоти (ФВЧ) розуміють фільтри (на L-C ланках), що пропускають на навантаження лише високі частоти: від до ∞. Смуга їх затухання знаходиться на інтервалі від 0 до .

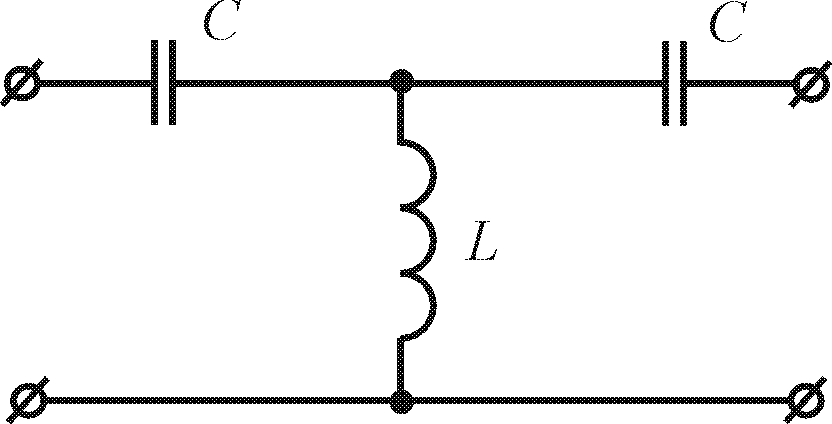
Схеми двох ФВЧ наведені на рис. 10.3, а, б. Характер зміни коефіцієнта затухання а і коефіцієнта фази b якісно зображають криві на рис. 10.3, в.

б

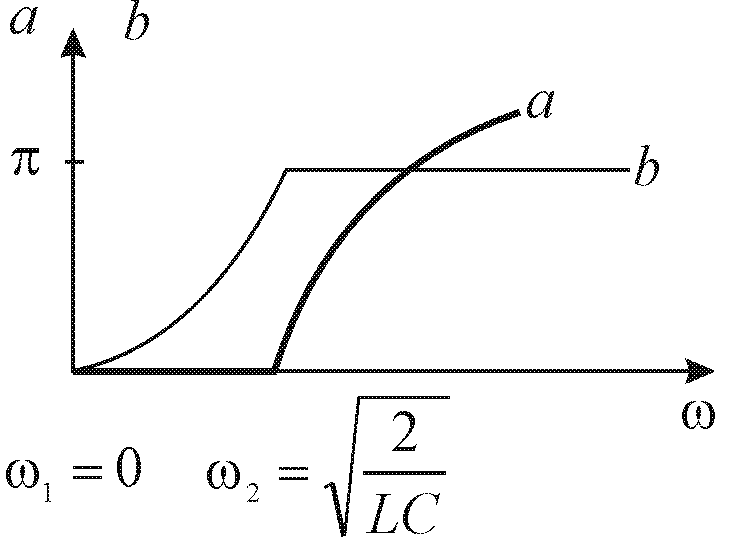
в

а – П - подібний ФНЧ;

б – Т - подібний ФНЧ;

в – характер зміни коефіцієнта затухання а і коефіцієнта фази b.

Рисунок 10.2 – Схеми ФНЧ на основі L-C ланок.

Розглянемо зміну величини характеристичного опору у смузі прозорості для Т-фільтра НЧ (рис. 10.2, а) і для Т-фільтра ВЧ (рис. 10.3, а), а також для П-фільтрів. З цією метою у вираз підставимо значення В і С у відповідності з формулами (10.3) – (10.10) і проаналізуємо отримані вирази.

Для Т-фільтра НЧ (рис. 1.2, а):

(10.28)

При Зі збільшенням частоти зменшується, спочатку мало відрізняючись від значення . При досягненні значення

Для П-фільтра НЧ (рис. 10.2, б):

(10.29)

Для Т-фільтра ВЧ (рис. 10.3, а):

(10.30)

В цьому випадку характер зміни відрізняється від характеру зміни для Т-фільтра НЧ, а саме:

при Зі збільшенням опір збільшується і при

Для П-фільтра ВЧ (рис. 10.3, б):

(10.31)

Якщо фільтр призначений для роботи на частотах, що знаходяться в середині смуги прозорості даного фільтра і відносно далеко відстаючих від значення , при якому , то опір навантаження на виході фільтрів НЧ вибирають рівним , який відповідає Для Т-фільтра НЧ (рис. 10.2, а)

а

б

в

а – П-подібний ФВЧ;

б –Т- подібний ФВЧ;

в – характер зміни коефіцієнта затухання а і коефіцієнта фази b.

Рисунок 10.3 – Схеми ФВЧ на основі L-C ланок.

Для фільтрів ВЧ звичайно навантаження узгоджують із значенням при . Для Т-фільтра ВЧ (рис. 10.3, а) У смузі (смугах) затухання виявляється чисто реактивним для всіх типів k-фільтрів.

Для того щоб виявити, індуктивний чи ємнісний характер має в смузі затухання, необхідно визначити характер вхідного опору цього фільтра для граничного режиму, а саме: для фільтрів НЧ (рис. 10.2, а, б) при дуже високій частоті, а для фільтрів ВЧ (рис. 10.3, а, б) при дуже низькій частоті (теоретично при ), вважаючи виходи схем закороченими. Аналогічний результат буде отриманий, якщо вважати їх розімкненими. В результаті визначимо, що в зоні затухання має індуктивний характер для Т-фільтра НЧ (рис. 10.2, а) і П-фільтра ВЧ (рис. 10.3, б) і ємнісний характер для П-фільтра НЧ (рис. 10.2, б) і Т-фільтра ВЧ (рис. 10.3, а).

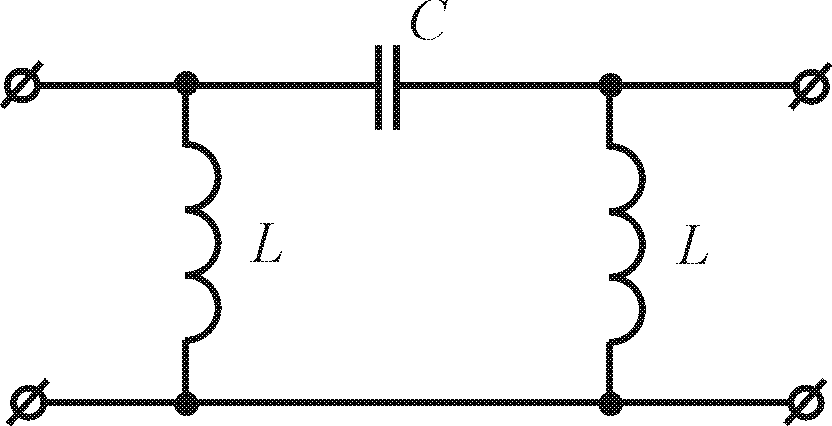
Смугові фільтри - це фільтри, що пропускають на навантаження лише вузьку смугу частот від до . Зліва від і справа від знаходяться смуги затухання. Схема простого смугового k-фільтра зображена на рис. 10.4, а. Параметри схеми повинні задовольняти умову

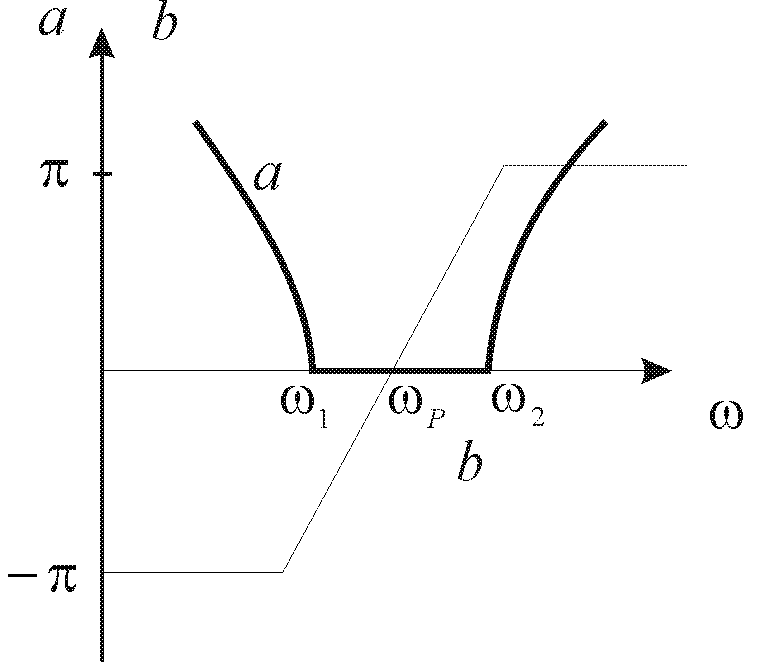
Характер зміни а і b для смугового фільтра зображають криві на рис. 10.4, б.

Формули для визначення параметрів смугового фільтра (рис. 10.4, а) за заданими частотами і і опором навантаження при резонансній частоті :

(10.32)

(10.33)

(10.34)

(10.35)

(10.36)

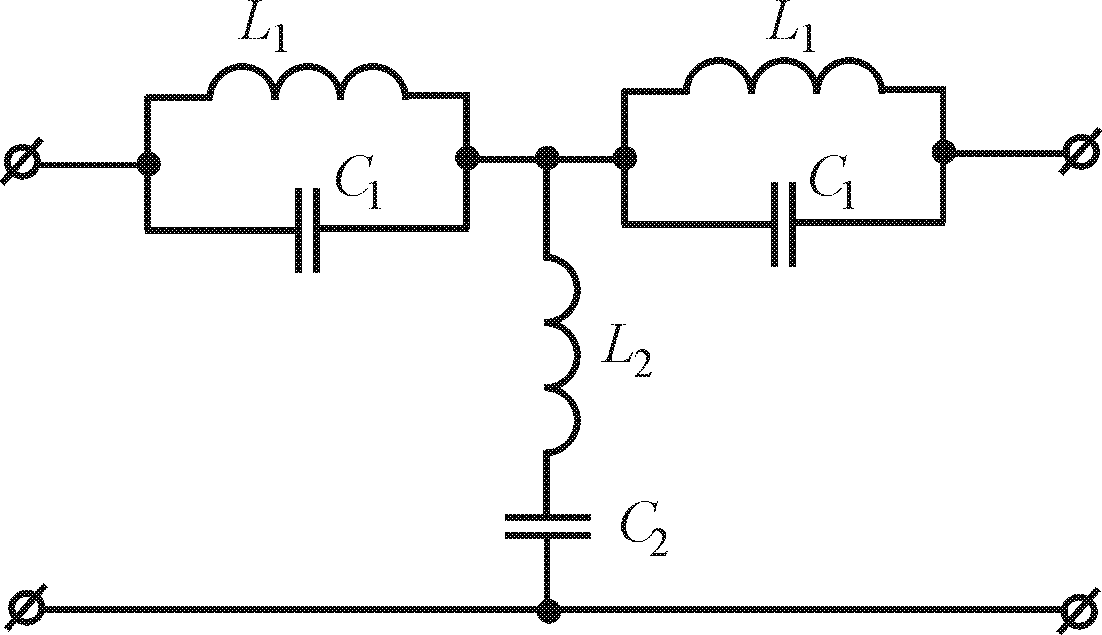
Під загороджувальними фільтрами (рис. 10.5, а) розуміють фільтри, в яких смуга прозорості наче розрізана на дві частини смуги затухання (рис. 10.5, б). Зліва від і справа від знаходяться дві частини смуги прозорості.

У схемі простого загороджуючого фільтра на рис. 10.5, а

Позначимо і і запишемо формули для визначення , і фільтрів, що на рисунку 10.4, а і 10.5, а.

Для рисунка 10.4, а:

(10.37)

(10.38)

Для рисунка 10.5, а:

(10.39)

(10.40)

а

б

а – Т-подібний смуговий фільтр;

б - характер зміни коефіцієнта затухання а і коефіцієнта фази b

Рисунок 10.4 – Схема смугового фільтра на основі L-C ланок.

Для фільтра (рисунок 10.4, а) в області частот від 0 до має ємнісний характер, а в області частот від до має індуктивний характер, а в області від до - ємнісний.

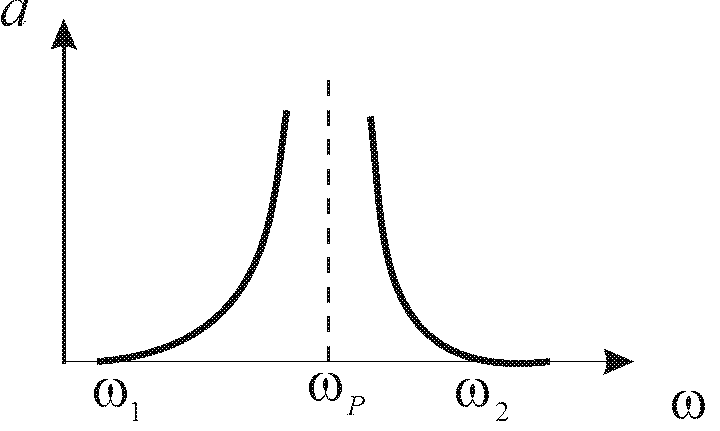
Характер зміни зображено кривими на рисунках 10.4, в і 10.5, в.

а

б

а – Т-подібний загороджувальний фільтр;

б - характер зміни коефіцієнта затухання а і коефіцієнта фази b

Рисунок 10.5 – Схема загороджувального фільтра на основі L-C ланок.

Якщо крутизна зміни коефіцієнта затухання якогось із описаних вище пасивних L-C фільтрів є недостатньою, то її можна підвищити, з’єднавши послідовно дві чи більше фільтруючих ланок. Однак, при цьому слід враховувати значне послаблення вхідного сигналу кожною з ланок пасивного фільтра.