2.6. Интерполяционная формула Ньютона при неравноотстоящих узлах

Используя понятие разделенных разностей, получим новую формулу для вычисления интерполяционного многочлена Лагранжа. Для этого представим многочлен Лагранжа в виде

. (2.22)

Очевидно, разность является многочленом степени , корнями которого являются узлы С учетом этого можно записать

Константу найдем, полагая . В результате получим

откуда

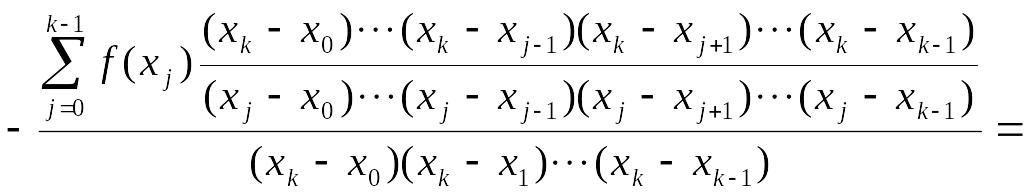
(2.23)

Последнее соотношение получено в силу формулы (2.21). Используя (2.23), соотношение (2.22) запишем в виде

(2.24)

Форма записи интерполяционного многочлена Лагранжа в виде (2.24) носит название интерполяционного многочлена Ньютона (формулы Ньютона) для неравноотстоящих узлов. В отличие от формулы Лагранжа формула Ньютона более удобна для вычислений, так как добавление одного или нескольких узлов не требует повторения всех вычислений.

Пример 2.4. Построить интерполяционный многочлен Ньютона для функции, приведенной в таблице 2.1.

Сначала получим таблицу разделенных разностей

Таблица 2.4.

		Разделенные разности 1-го порядка	Разделенные разности 2-го порядка
0	1
1	2
2	4

Выполнив расчеты по формуле (2.24), получим:

.

В силу того, что формула Лагранжа и формула Ньютона являются различными аналитическими представлениями многочлена Лагранжа то в качестве остаточного члена формулы Ньютона можно взять остаточный член в виде (2.12).

Получим новую форму остаточного члена многочлена Лагранжа. Для этого рассмотрим формулу для разделенной разности порядка, построенной по узлам , где – точка, в которой вычисляется многочлен Лагранжа. Эта формула в силу (2.21) имеет вид:

. (2.25)

Выразив из (2.25) получим

, (2.26)

где – формула Лагранжа. Тогда из (2.26), учитывая что остаточный член , получим новую формулу для остаточного члена формулы Ньютона:

. (2.27)

Формулу связи разделенной разности с производной получим, приравнивая правые части (2.27) и (2.12), при этом переобозначив точку , как и учитывая свойство симметричности для разделенных разностей. Тогда имеем:

. (2.28)

В тех случаях, когда плавно изменяющаяся на интервале функция, учитывая свойство разделённой разности (2.28), погрешность метода (2.16) можно приближенно оценить выражением

. (2.29)

Заметим, что для того чтобы вычислить разделенную разность, входящую в формулу (2.29), необходимо задать дополнительный узел и иметь значение функции в этом узле. Для оценки погрешности (2.29), в отличие от (2.12), уже не требуется знания функции , подлежащей интерполированию, здесь достаточно иметь только табличные значения этой функции.