1.8. Контрольные вопросы

1. Как определяются математические оценки точности приближенного числа?

2. Чему равна относительная погрешность числа, записанного в двоичной системе, если число разрядов равно и порядок равен ?

3. Чем обусловлена погрешность метода?

4. Чем обусловлена неустранимая погрешность?

5. Чем обусловлена погрешность округления?

6. Как определяется погрешность числа, заданного с верными знаками в узком смысле?

7. Записать число c верными знаками в узком смысле, если оно задано с погрешностью .

8. Записать число c верными знаками в узком смысле, если оно задано с погрешностью .

9. Чему равна абсолютная погрешность в узком смысле числа 5,4563 заданного с верными знаками?

10. Записать число c верными знаками в узком смысле, если оно задано с погрешностью .

11. Чему равна абсолютная погрешность функции многих переменных ( – абсолютные погрешности аргументов)?

12. Чему равна относительная погрешность функции многих переменных ( – относительные погрешности аргументов)?

13. Относительная погрешность функции многих переменных зависит от чувствительностей, что определяют чувствительности?

14. Как определяется абсолютная и относительная погрешности разности двух чисел?

15. Что необходимо предпринимать при вычитании двух близких чисел?

16. Как решается обратная задача в теории погрешностей?

17. Как определяются абсолютная и относительная погрешность произведения?

18. Как определяются абсолютная и относительная погрешность частного?

19. Как определяются абсолютная и относительная погрешность возведения в степень?

20. Как определяются абсолютная и относительная погрешность при взвешенном суммировании?

1.9. Задания к главе 1

Задание 1.1. Определить:

- для п.п. а) и б) число верных знаков приближенного числа, если известна абсолютная погрешность;

- для п. в) определить абсолютную и относительную погрешность, если известно число верных знаков;

- для п. г) определить абсолютную погрешность , если известны абсолютные погрешности аргументов , . Значение функции записать с верными знаками.

Варианты исходных данных приведены в п. 5.1.

2. Аппроксимация функций

2.1. Постановка задачи

Пусть в результате эксперимента для некоторой функции получены значения , …, , т.е. задана таблица значений , . Такие таблицы могут быть построены в различных предметных областях. Например, в технике таблица может быть построена по показаниям измерительных приборов, в экономике таблица может являться результатом анализа экономической деятельности фирмы.

На практике наиболее часто встречаются следующие задачи:

- найти значение функции в некоторой точке такой, что

- найти значение по заданному значению функции , , ;

- найти значения производных в точке ;

- найти значение интеграла

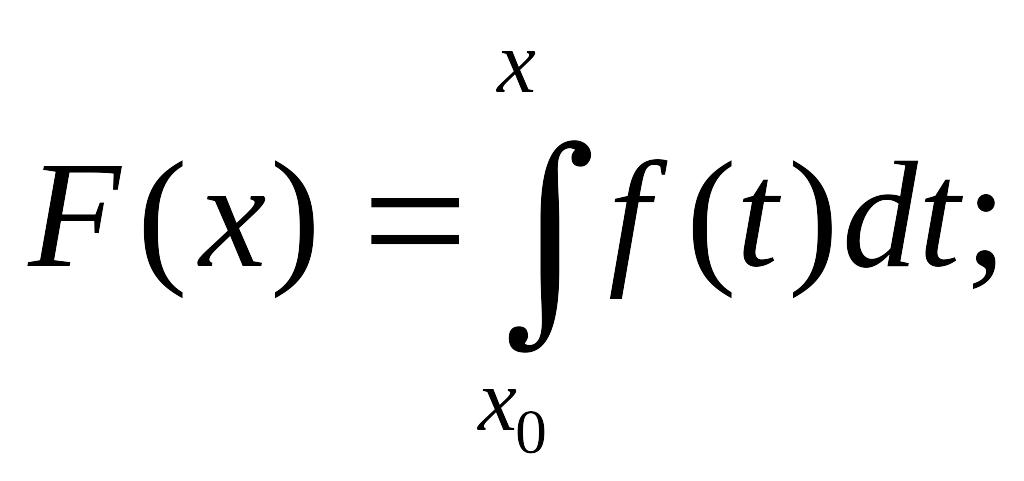
- найти для функции , заданной таблично, приближенное аналитическое выражение.

Решения перечисленных задач можно найти, построив для функции интерполяционную функцию .

Отметим, что эти задачи имеют смысл и в том случае, если аналитическое выражение функции известно, но оно очень сложное. В этом случае функцию табулируют и строят для нее интерполяционную функцию. Таким образом, можно получить более простое приближенное аналитическое выражение для функции , которое затем использовать в вычислениях.

Рассмотрим требования, которым должна удовлетворять интерполяционная функция. Пусть – множество вещественных функций, заданных на отрезке . Зададим на множестве счетную систему функций . Построим функцию

(2.1)

где – некоторые, подлежащие определению вещественные коэффициенты. Система функций должна быть линейно независимой. Потребуем, чтобы в точках значения функции совпадали со значениями функции , т.е.

(2.2)

Условие (2.2) – основное требование, которое используется при построении интерполяционных функций. В этом случае функция вида (2.1) называется интерполирующей, а точки – узлами интерполирования. В силу требования (2.2) будем иметь систему линейных уравнений для определения коэффициентов :

. (2.3)

Перепишем систему (2.3) в векторно-матричном виде:

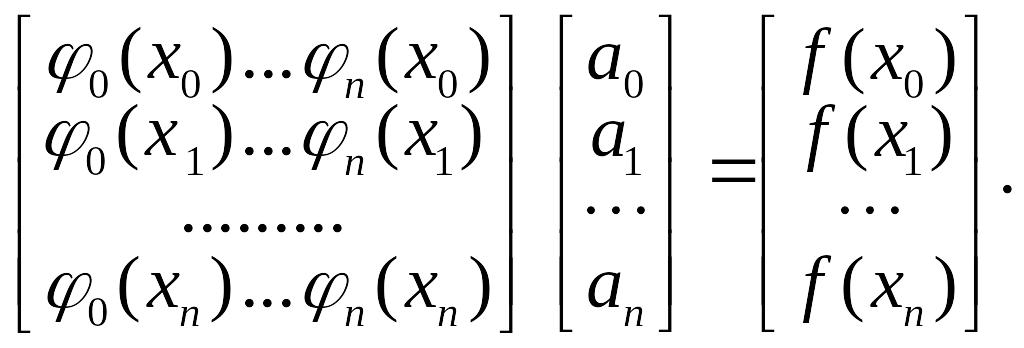(2.4)

Система уравнений (2.4) имеет единственное решение, если определитель матрицы системы не равен нулю, т.е.

.

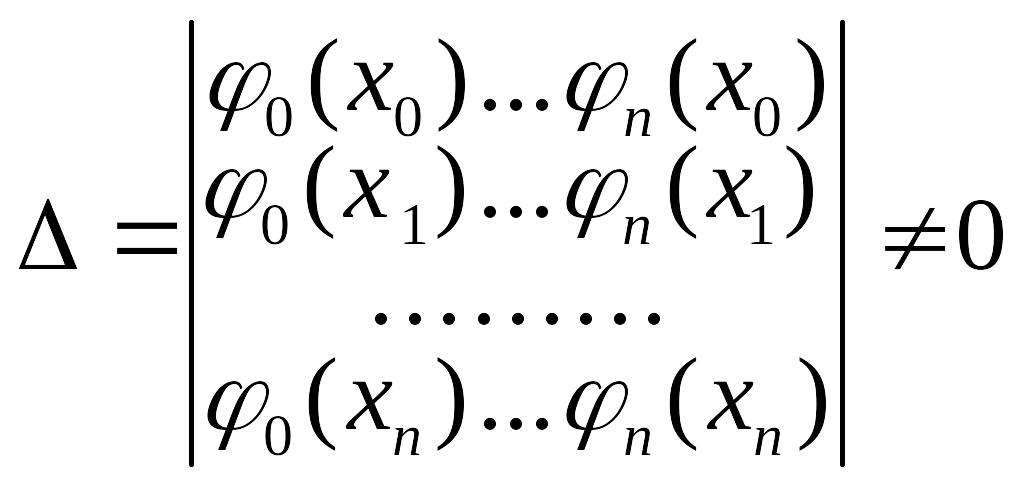Система функций , для которой при всех где называется системой Чебышева.

Таким образом, первое условие, которое накладывается на функции , заключается в том, что должны составлять систему Чебышева.

Второе условие, которому должна удовлетворять система функций является условием полноты.

Поясним это условие. Пусть  – класс интерполируемых функций и . Семейство линейных комбинаций вида (2.1) называется полным в классе , если для всякой функции и любого существует такое и такие коэффициенты что для всех справедливо неравенство

Отметим также, что для построения аппроксимирующих функций, кроме интерполяционной функции, построенной на основе условия (2.2), используются приближения, минимизирующие сумму квадратов отклонений аппроксимирующей функции от заданных табличных значений (см. метод МНК п. 2.14 и п. 2.15.3), и метод аппроксимации с помощью сплайн-функций (см. п. 2.13).