4.9.2. Геометрический метод Монте-Карло

Пусть при вычислении интеграла

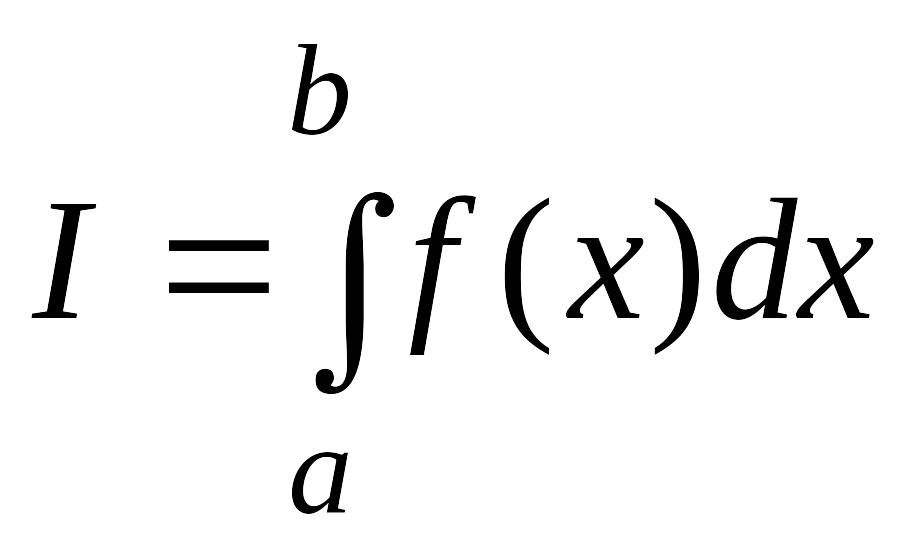(4.63)

для подынтегральной функции на выполняется условие:

.

Введем новую функцию

,

значение которой лежат в интервале . Тогда

.

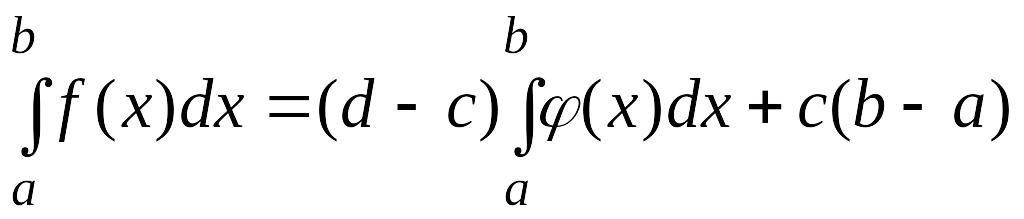Затем, выполнив замену переменной , получим

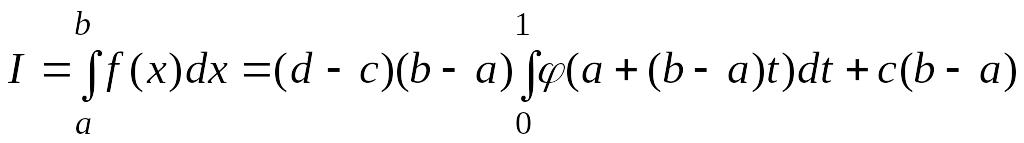. (4.64)

Таким образом, необходимо вычислить интеграл

,

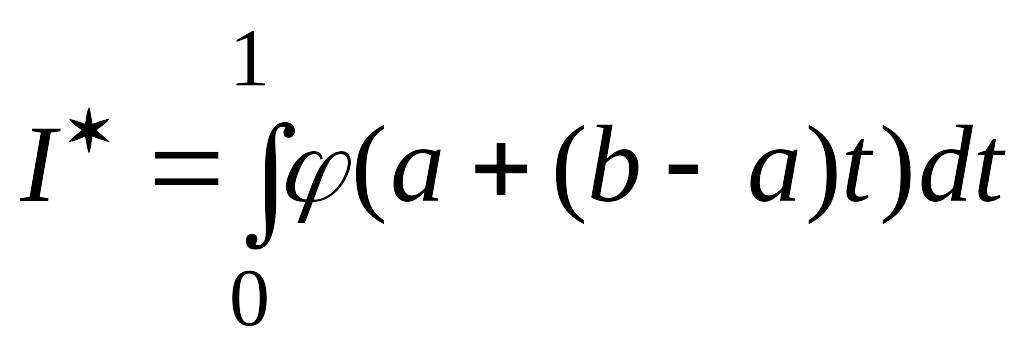а затем получить значение исходного интеграла , согласно (4.64).

Для реализации метода генерируется точек , где − независимые случайные величины, равномерно распределенные на интервале . Если для совокупности двух случайных величин окажется, что

,

то событие считается неблагоприятным; если

,

то событие считается благоприятным, так как в этом случае точка попадает в заштрихованную область (рис.4.1).

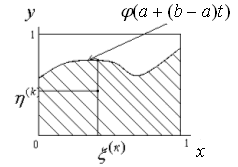
Рис. 4.1. Графическая иллюстрация геометрического метода

Пусть из точек попали в заштрихованную область. Частота попадания будет приблизительно равна площади заштрихованной области, т.е.

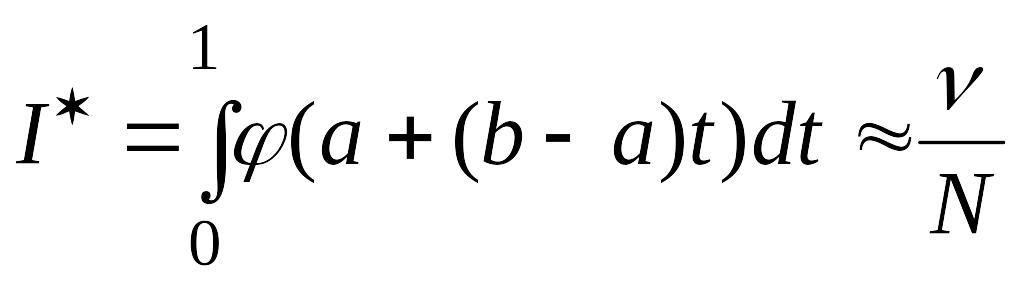. (4.65)

Окончательно, значение интеграла (4.63) определяется согласно выражению (4.64) с учетом формулы (4.65).

Пусть требуется вычислить интеграл

, (4.66)

где область интегрирования определяется неравенствами (4.52). При этом требуется, чтобы для подынтегральной функции в области выполнялось условие

. (4.67)

Сделаем замену переменных

,

с помощью которых область преобразуется в область и заключается в -мерный единичный куб. Тогда интеграл (4.66) запишется в виде

, (4.68)

где

,

а область определяется неравенствами (4.54).

Введем новые функции

и

Тогда

. (4.69)

Для вычисления интегралов в (4.69) генерируется точек где независимые случайные величины, равномерно распределенные на интервале . Для первого интеграла соответствует числу благоприятных событий, если выполняются неравенства

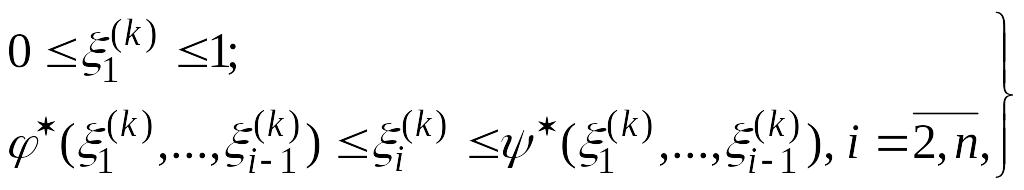(4.70)

а соответствует числу благоприятных событий для второго интеграла, если выполняются неравенства (4.70) и

. (4.71)

Тогда, согласно (4.59), значение интеграла будет равно

. (4.72)

Как и в простейшем методе Монте-Карло, здесь точность вычисления интеграла и число испытаний взаимосвязаны.

Рассмотрим подход к определению значения , который обеспечивает требуемую точность вычисления .

Пусть требуется вычислить интегралы:

(4.73)

или

, (4.74)

где область заключена в -мерный единичный куб и для значений подынтегральных функций выполняются неравенства:

,

.

Погрешность вычисления интеграла можно определить, воспользовавшись неравенством Чебышева

, (4.75)

где ─ малая величина, обычно . Формула (4.75) означает, что с вероятностью погрешность вычисления интегралов с помощью геометрического метода Монте-Карло приблизительно равна , при этом значение можно определить из неравенства

. (4.76)

Пример 4.15. Требуется вычислить интеграл

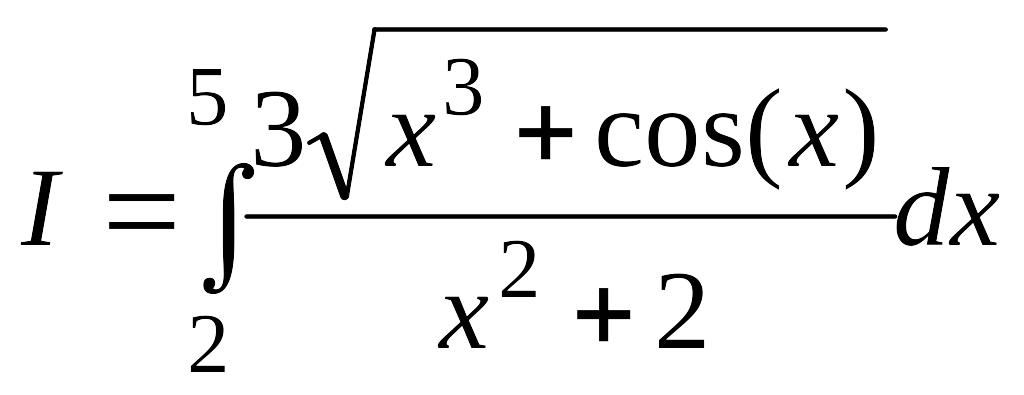
с точностью методами Монте-Карло.

1. Простейший метод Монте-Карло.

Сделаем замену переменных , где . Тогда

.

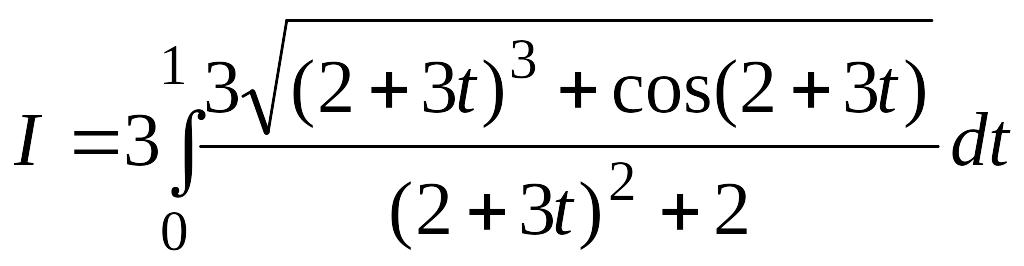При вычислении интеграла получаются следующие результаты: .

2. Геометрический метод Монте-Карло.

Подынтегральная функция

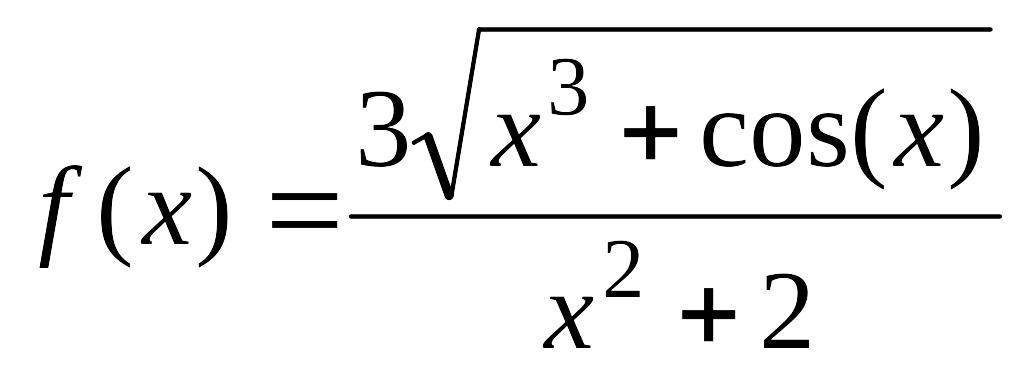
на интервале принимает минимальное значение и максимальное значение . Вводим новую функцию

и делаем замену переменных . Тогда

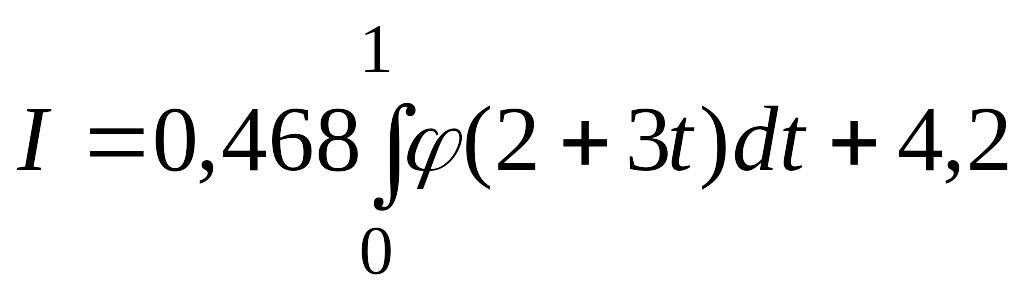
и при вычислении интеграла получаются следующие результаты: .

Заметим, что геометрический метод Монте-Карло всегда требует значительно большее число испытаний, чем простейший.

Пример 4.16. Требуется вычислить интеграл

с точностью методами Монте-Карло от функции . Область определяется неравенствами:

где

.

1. Простейший метод Монте-Карло.

Так как для , то с помощью замены переменных , область преобразуется в область , которая определяется неравенствами

где

.

При этом область оказывается заключенной в единичный квадрат (см. рис.4.2., где сплошной линией изображен график функции , а пунктирной − ).

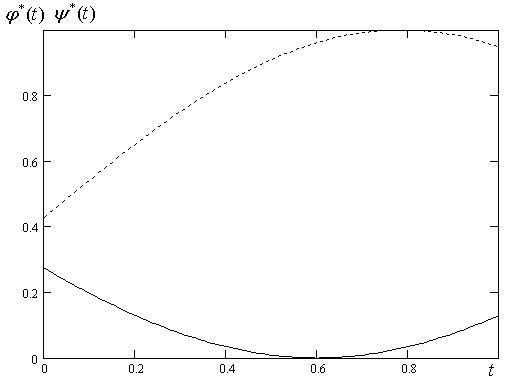
Рис. 4.2. Преобразованные границы области интегрирования

Тогда исходный интеграл запишется в виде:

,

где и

.

На рис.4.3. изображена область, объем которой равен .

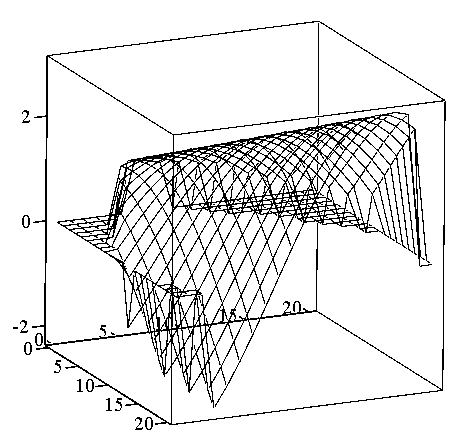
Рис.4.3. Графическое представление функции

В результате получается, что значение интеграла , при этом .

2. Геометрический метод Монте-Карло.

Для функции в области выполняется неравенство: . Исходный интеграл, как и в простейшем случае, приводится к виду

.

Затем вводятся новые функции

и

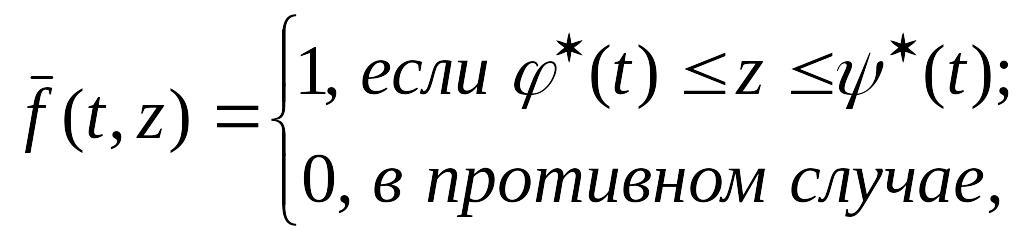
и интеграл записывается в виде

,

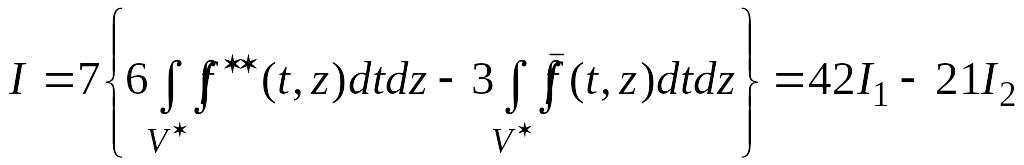где

.

На рис.4.4. и 4.5. изображены области, заключенные в единичный куб, объем которых равен и соответственно.

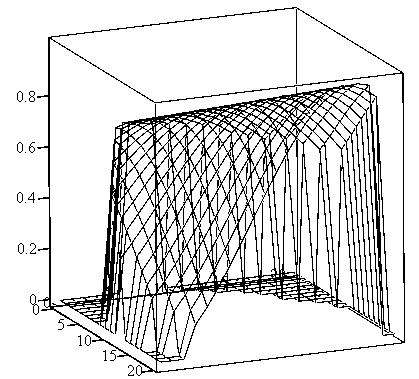
Рис.4.4. Графическое представление функции

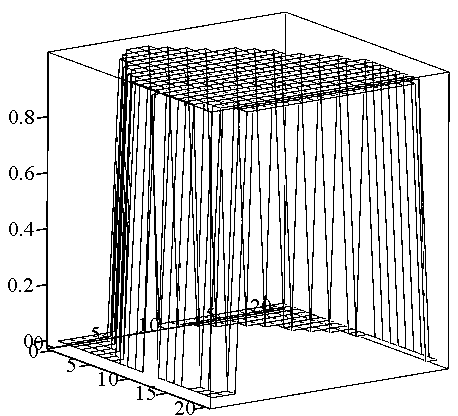
Рис.4.5. Графическое представление функции

Согласно геометрическому методу Монте-Карло, интеграл вычисляется следующим образом

.

Значение определяется из неравенства

,

где . Откуда получаем, что наименьшее значение , удовлетворяющее этому неравенству . Значение интеграла получается равным , при этом , а .