1. Основы теории погрешностей

1.1. Математические оценки точности приближенного числа

Введем обозначения:  – точное значение числа,  – приближенное значение число,  – погрешность числа (ошибка),  – модуль ошибки. В силу того, что точное значение , как правило, неизвестно вводится понятие абсолютной погрешности числа .

Абсолютной погрешностью числа называется наименьшее из всех возможных чисел , которого не превышает модуль ошибки

.

Для того, чтобы характеризовать точность вычислений (измерений) вводится понятие относительной погрешности, определяющей величину погрешности, которая приходится на единицу измеряемой величины

.

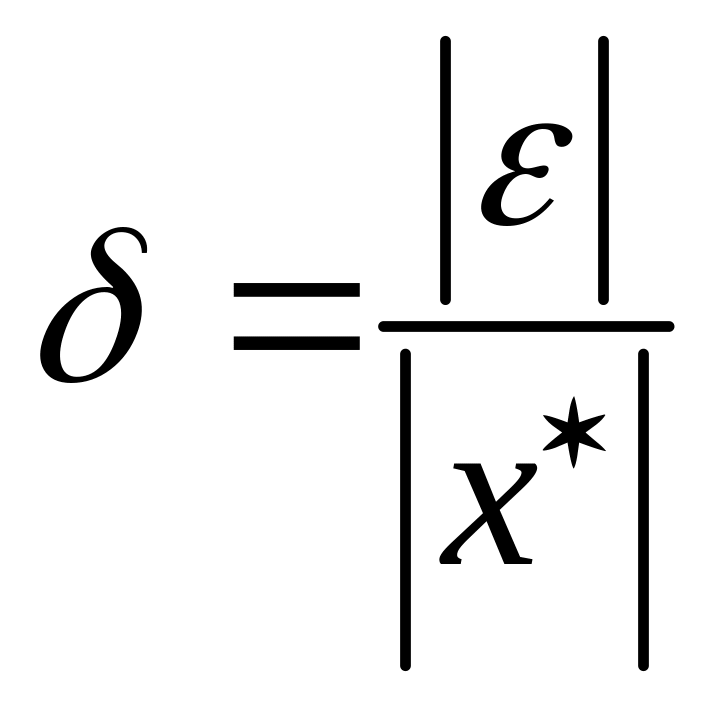На практике используют следующую оценку относительной погрешности

.

1.2. Запись чисел на эвм

При записи чисел в ЭВМ применяется двоичная система счисления, используемая для представления любого числа с плавающей запятой

,

Здесь p – порядок, m – длина разрядной сетки. Типичное значение параметра , определяющее границу для порядка и параметра n равно:

В десятичной системе счисления порядок и число знаков определяются равенствами:

При вводе числа в ЭВМ, его обычно округляют и приближенно записывают в виде

.

Абсолютная погрешность такой записи числа не больше единицы последнего разряда в , то есть:

.

При этом относительная погрешность числа равна:

.

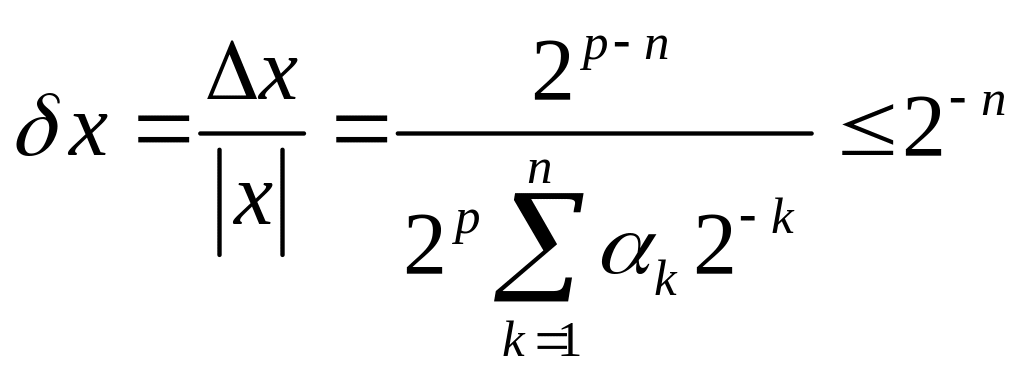1.3. Верные знаки приближенного числа

Приближенные числа принято записывать с верными знаками. Если – основание системы счисления ( – обычно равно 2, 3, 8, 10, 16), то число может быть представлено в виде

.

Приближенное число имеет верных знаков, если для абсолютной погрешности справедливо неравенство

.

Для десятичной системы счисления ( =10), если =0,5 , то число имеет n верных знаков в узком смысле

, (1.1)

если =1,0, то число имеет n верных знаков в широком смысле. Если число имеет n верных знаков, то цифры называются сомнительными.

Относительная погрешность числа, содержащего n верных знаков, определяется соотношением

На практике обычно используется понятие числа с верными знаками в узком смысле. Тогда можно сказать, что абсолютная погрешность числа с верными знаками равна половине последнего правильного разряда. Отметим также, что при записи числа с верными знаками необходимо пользоваться правилами округления чисел.

Пример 1.1. Записать с верными десятичными знаками в узком смысле значение числа , если оно задано с погрешностью . Для решения задачи необходимо сначала определить значение , оно в нашем случае равно -3. Затем необходимо для погрешности записать неравенство

,

в котором справа должна стоять минимально возможная целая степень. Далее в силу формулы (1.1) составляется уравнение

,

решение, которого дает количество верных знаков числа. Очевидно . Тогда, записанное с верными знаками число с учетом правил округления, имеет вид

.

1.4. Классификация погрешностей

Существуют три основных типа погрешностей.

1. Неустранимая погрешность – это погрешность, обусловленная неточностью исходных данных и несоответствием математической модели реальному процессу.

2. Погрешность метода – возникает при замене исходной математической задачи на аппроксимирующую задачу. Необходимость такой замены обусловлена тем, что часто исходную задачу точно невозможно решить из-за ограниченного быстродействия ЭВМ, а также из-за ограниченности памяти.

3. Погрешность округления обусловлена ограниченной разрядной сеткой, используемой при представлении чисел в ЭВМ. Округление данных производится также при их вводе в ЭВМ, при выполнении арифметических операций и при выводе данных.

Рассматривается также полная погрешность , которая обусловлена всеми перечисленными выше факторами. На практике же, полную погрешность оценивают как сумму неустранимой погрешности и погрешности метода

.

Для вычислительно устойчивых алгоритмов влиянием погрешности округления обычно пренебрегают.

При решении задач нет смысла применять численный метод с погрешностью метода, существенно меньшей, чем значение неустранимой погрешности. Это означает, что погрешность метода должна быть согласована с неустранимой погрешностью.