4.2.2. Квадратурная формула трапеций

Для формулы трапеций Два равноотстоящих узла на образуют точки и . Формула трапеций и выражение для погрешности имеют вид

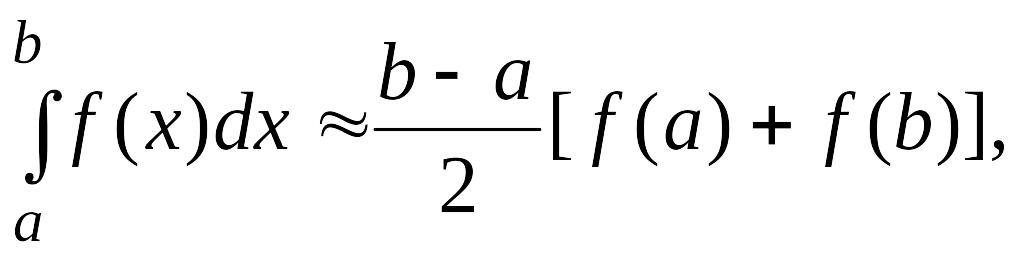(4.17)

.

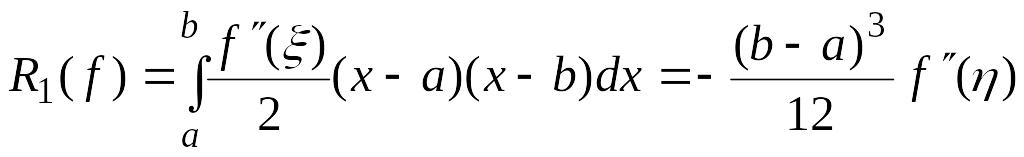Последнее выражение для получается в предположении, что непрерывна на и произведение не меняет знак на .

Геометрически формула (4.17) означает, что площадь, ограниченная кривой на , заменяется площадью трапеции с основанием и высотой .

Разделив отрезок на частей, применив к каждой части формулу трапеций и просуммировав результаты, получим обобщенную формулу трапеций

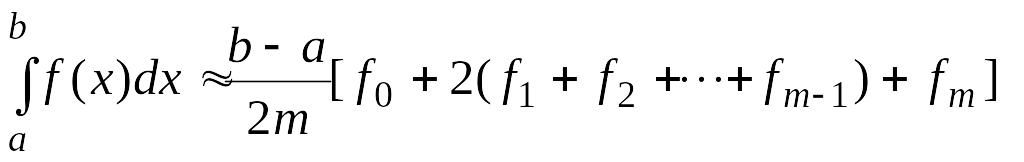. (4.18)

Погрешность обобщенной формулы трапеций имеет вид

.

4.2.3. Квадратурная формула Симпсона (парабол)

В этом случае Три равноотстоящих узла на образуют точки . Квадратурная формула Симпсона имеет вид

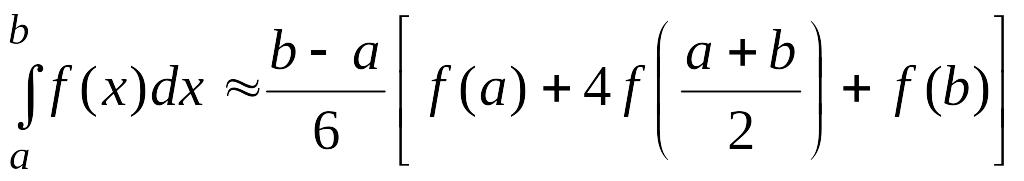. (4.20)

Геометрически формула (4.20) означает, что площадь, ограниченная кривой на , заменяется площадью, ограниченной параболой, построенной на по трем точкам .

Так как средняя точка интервала является узлом квадратурного правила, то формула (4.20) является точной для многочленов третьей степени. Для нахождения погрешности квадратурной формулы Симпсона построим многочлен Эрмита третьей степени , удовлетворяющий условиям:

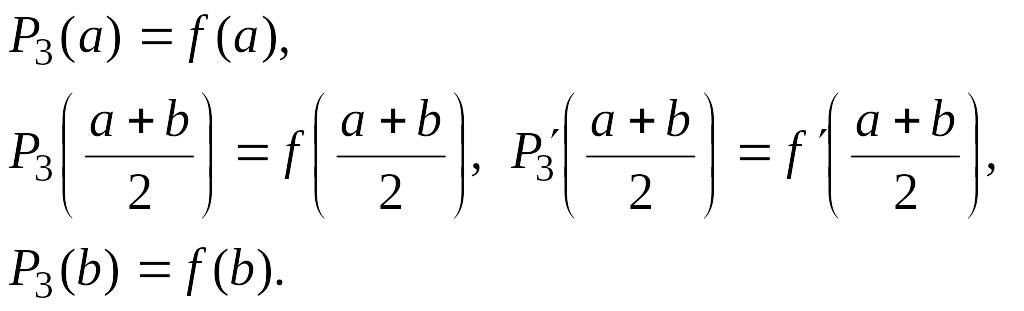
Остаточный член многочлена Эрмита имеет вид:

.

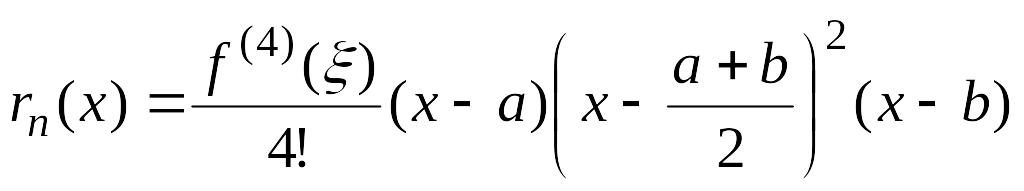Тогда остаточный член квадратурного правила Симпсона можно вычислить следующим образом:

.

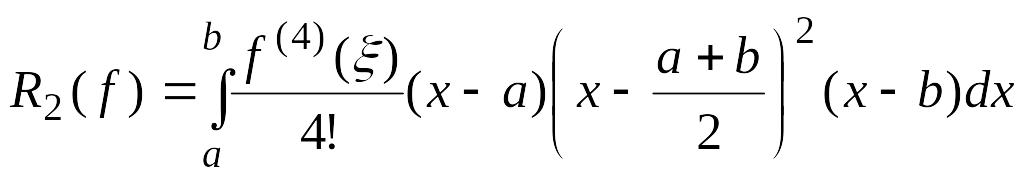Так как множитель 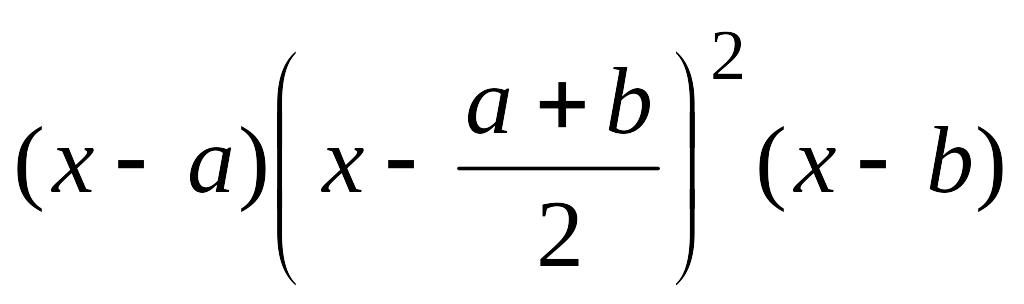не меняет знак на и, в предположении о непрерывности на , существует такая точка такая, что

Разделим отрезок на четное число частей длиной и к сдвоенному отрезку применим формулу (4.20). Тогда

.

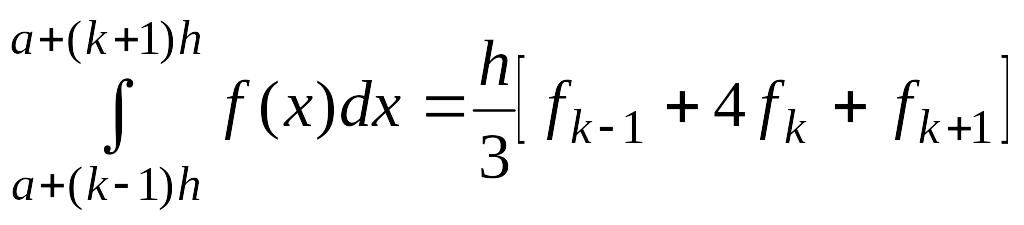Просуммировав результаты по всем сдвоенным отрезкам на , получим обобщенную формулу Симпсона

, (4.21)

погрешность которой можно представить в виде

,

где .

Ввиду предположения о непрерывности на , существует такая точка , что

.

Тогда выражение для погрешности квадратурной формулы (4.21) примет вид

(4.22)

4.2.4. Квадратурная формула “трех восьмых” (формула Ньютона)

Квадратурные коэффициенты формулы “трех восьмых” равны

.

Четыре равноотстоящих узла на образуют точки . В этом случае квадратурная формула “трех восьмых” и ее погрешность имеют вид

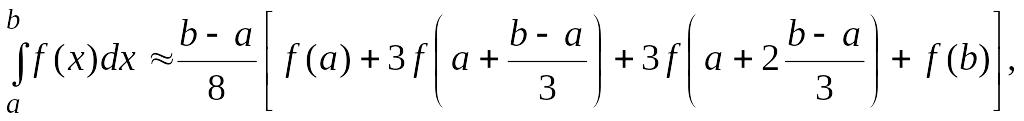
Геометрически эта формула означает, что площадь, ограниченная кривой на , заменяется площадью, ограниченной многочленом, который построен на по четырем точкам .

Разделив отрезок на число частей , кратное трем, применив к строенным отрезкам формулу “трех восьмых” и просуммировав результаты, получим обобщенную формулу “трех восьмых”

. (4.23)

Погрешность квадратурной формулы “трех восьмых” определяется выражением

(4.24)

Пример 4.1. При вычислении интеграла

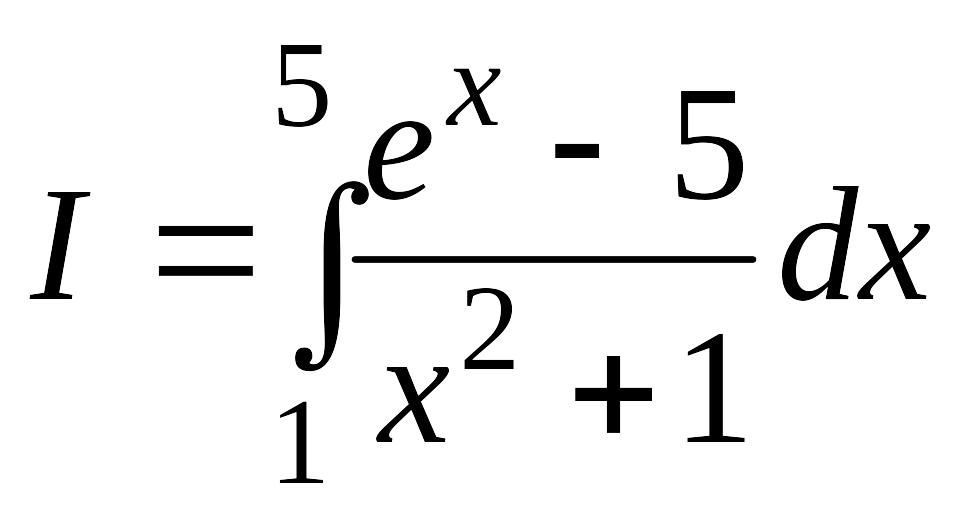
по обобщенным формулам Ньютона-Котеса для различных получаются следующие результаты (таблица 4.1)

Таблица 4.1.

	Квадратурная формула
1	левых прямоугольников	5,9006533	6,7233212	6,997838
2	правых прямоугольников	8,1195699	7,2780504	7,0022759
3	средних прямоугольников	6,9950321	2 6,9997426	7,0000569
4	трапеций	7,1548715	7,0791071	7,0008164
5	Симпсона	7,0000437	7,0000571	7,0000569
6	«трех восьмых»	6,9999482	7,0000573	7,0000569

Полученные результаты показывают, что, при вычислении интеграла с заданной точностью , для каждой квадратурной формулы необходимо задавать свое значение .