2.15. Аппроксимация функций многих переменных
При
решении задач обработки данных часто
возникает задача аппроксимации функций
многих переменных
.
В частном случае для функции двух
переменных
,
можно задать эту функцию в виде следующей
таблицы:
Таблица 2.14.
Здесь
,
а узлы
,
,
,
могут быть как неравноотстоящими так
и равноотстоящими (
,
).
Кроме того точки на плоскости могут
быть расположены достаточно произвольно
(некоторые ограничения на расположение
точек все таки должны выполняться (см.
ниже)), тогда их удобно обозначать
следующим образом:
.
2.15.1. Построение интерполяционных многочленов
Рассмотрим задачу построения многочлена первой степени по двум переменным:
.
(2.155)
Потребуем,
чтобы значение многочлена со значениями
функции
совпадали в трех точках
(
).
(2.156)
Тогда
значения коэффициентов
,
,
определятся из системы линейных
алгебраических уравнений
,
которая в векторно-матричном виде имеет вид:
.
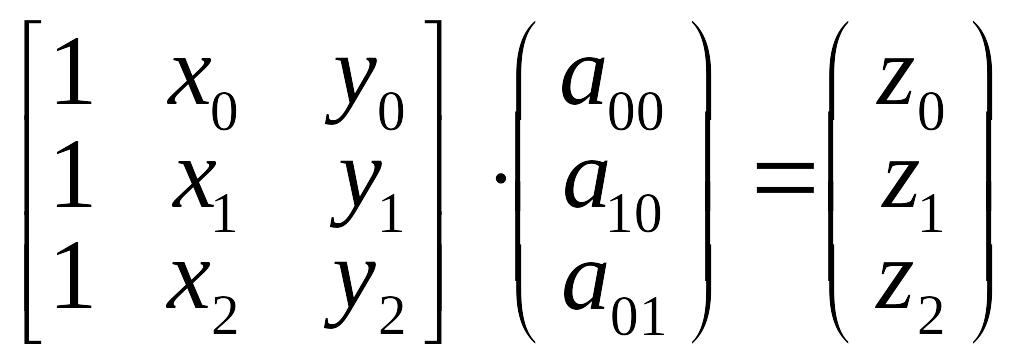Решение
этой системы существует и является
единственным, если три точки
,
и
не лежат на одной прямой, так как в этом
случае определитель матрицы системы
не равен нулю.
Многочлен второй степени для двух переменных имеет вид:
.
(2.156)
Тогда, если заданы значения функции в шести точках
(
),
(2.157)
то
можно сформировать систему линейных
алгебраических уравнений для определения
коэффициентов
,
,
,
,
,
.
Эта система в векторно-матричном виде
будет иметь вид:
.
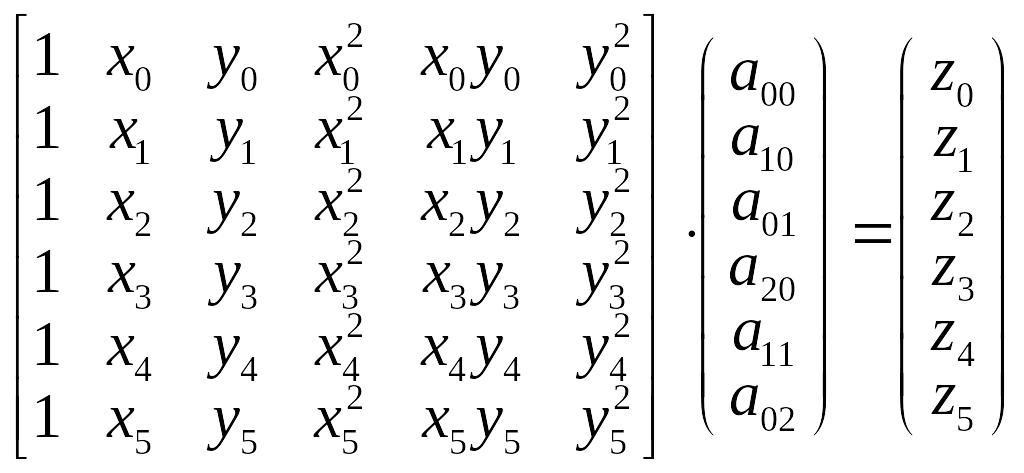(2.158)
Решение системы (2.158) будет существовать и является единственным, если 6 точек ( ) ( ) не лежат на кривой 2-го порядка.
По аналогии можно построить интерполяционный многочлен для двух переменных степени
.
(2.159)
Число
неизвестных коэффициентов в этом случае
равно
.
Число узлов должно быть такое же. Если
велико, то для построения многочлена
необходимо решить систему линейных
алгебраических уравнений высокого
порядка. Если число узлов меньше чем
,
то часть коэффициентов приходится
задавать произвольно, а это приведет к
потере точности.
В
случае, когда исходные данные даны в
виде таблицы 2.14. можно вычислить значение
интерполяционного многочлена степени
(
)
по формуле
Лагранжа
(узлы по переменным
и
могут быть неравноотстоящими):
.
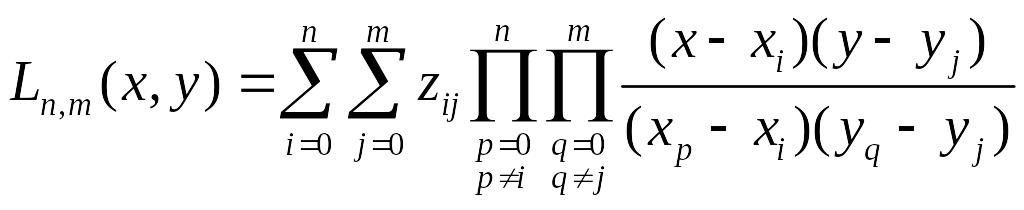(2.160)
Пользоваться этой формулой достаточно неудобно и поэтому она редко используется. Кроме того, возникают существенные трудности при оценке остаточного члена, так как в этом случае теорема Ролля не будет справедлива.
Можно
также построить интерполяционные
многочлены Ньютона. В частном случае,
когда узлы в таблице 2.14 равноотстоящие
и
,
,
построим интерполяционный многочлен
Ньютона 2-ой степени для двух переменных.
Этот многочлен будет иметь вид:
.
(2.161)
Здесь
,
и по аналогии с конечными разностями
используются частные конечные разности
первого и второго порядка:
.