2.14.2. Аппроксимация ортогональными полиномами
Лучшие по точности результаты при аппроксимации можно получить, если использовать в качестве базисных функций классические ортогональные полиномы Чебышева, Лежандра, Лагерра, Якоби и др.
Полиномы называются ортогональными, если существует некоторый интервал , на котором
,
(2.141)
где
весовая функция.
В случае большого количества узлов на значения интегралов (2.141) будут близки к дискретным скалярным произведениям (2.134), так как интегрирование можно приближенно заменить суммированием. В этом случае недиагональные элементы матрицы Грама будут небольшими по абсолютной величине, что уменьшает погрешность решения системы нормальных уравнений.
Для наиболее
гладкого представления экспериментальных
данных (с минимальным числом и амплитудой
выбросов) в качестве базисных функций
выбирают ортогональные полиномы Чебышева
,
которые определены и ортогональны на
интервале
с весовой функцией
.
Для задания полиномов Чебышева используется рекуррентная формула (2.31).
Так как в многочленах
Чебышева
коэффициент при старших степенях
равен
(см.
п. 2.8, свойство 1) , то это не всегда удобно
при оценке вклада в аппроксимирующую
функцию
старших степеней
по величине коэффициентов
.
В этом случае полиномы Чебышева можно
ввести и по другой рекуррентной формуле,
позволяющей построить приведенные
многочлены Чебышева:
,
(2.142)
где
,
.
Полиномы
ортогональны на интервале
с такой же весовой функцией, что и
.
Весовую функцию, равную единице на интервале , имеют полиномы Лежандра, которые определяются по следующей рекуррентной формуле:
,
(2.143)
где
,
.
Интервал [
],
где заданы узлы таблицы данных
,
переводится в интервал
,
где определены и ортогональны полиномы
Чебышева и Лежандра с помощью линейного
преобразования:
.
(2.144)
2.14.3. Аппроксимация ортогональными полиномами дискретной переменной
Если построить
систему базисных функций
таким образом, чтобы обращались в нуль
скалярные произведения на дискретном
множестве узловых точек, то матрица
Грама будет диагональной и можно избежать
численного решения системы нормальных
уравнений. В зависимости от распределения
погрешности обрабатываемых данных
можно построить ортогональные полиномы
дискретной переменной с соответствующими
дискретными весовыми функциями
,
.
Из классических ортогональных
полиномов
дискретной
переменной
известны полиномы Хана,
Мейкснера, Кравчука,
Шарлье.
Рассмотрим алгоритм
построения полиномов Чебышева
дискретной переменной, которые являются
частным случаем полиномов Хана с
единичной весовой функцией.
Полагаем:
(2.145)
,
(2.146)
и
неизвестный коэффициент
определим из условия ортогональности
и
,
то есть
или
.
(2.147)
Откуда
.
(2.148)
Полином второй
степени также представляется в общем
виде с неопределенными коэффициентами
и
:
.
(2.149)
Коэффициенты
и
найдем из условия ортогональности
полиномов
,
то есть
,
и т.д.
Для полиномов Чебышева дискретной переменной существует двухслойная рекуррентная формула, по которой можно вычислить полином любой степени, зная :
,
(2.150)
где
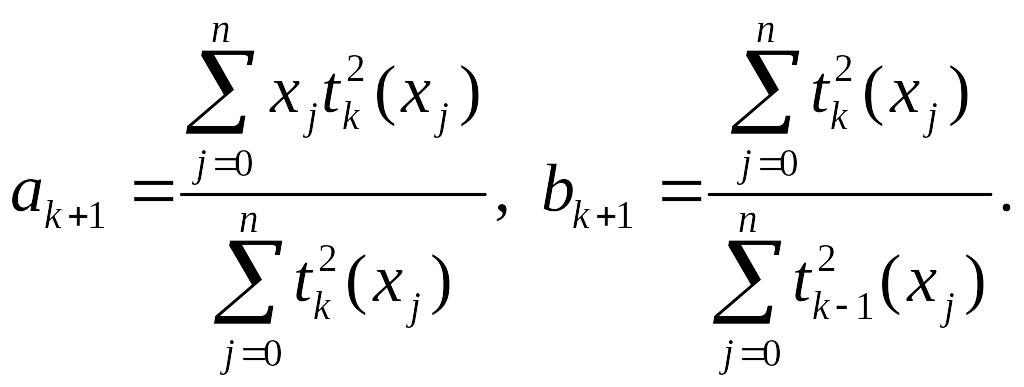(2.151)
Аппроксимирующая функция определяется, как и ранее, в виде линейной комбинации базисных функций, в качестве которых берутся полиномы Чебышева дискретной переменной :
.
(2.152)
Тогда, так как матрица Грама является диагональной, коэффициенты этой линейной комбинации определяются как частное от деления правых частей получающейся системы нормальных уравнений на диагональные элементы этой матрицы, то есть:
.
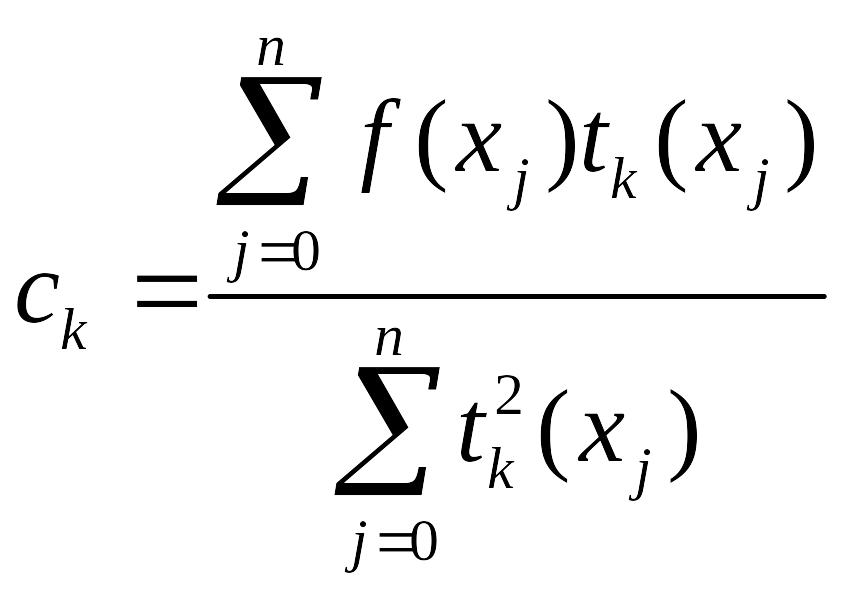(2.153)
Заметим, что если для улучшения качества аппроксимации возникает необходимость в увеличении числа базисных функций, то не придется пересчитывать коэффициенты , определенные с меньшим значением m.