2.9. Многочлены наилучшего равномерного приближения

Введем абсолютное отклонение аппроксимирующего многочлена от аппроксимируемой на интервале непрерывной функции

. (2.42)

Если многочлен выбран отрезке так, что отклонение минимально, то называется многочленом наилучшего равномерного приближения. Точки, в которых реализуется максимальное отклонение многочлена от называются точками чебышевского альтернанса.

Отметим, что существование и единственность многочлена наилучшего равномерного приближения на ограниченном отрезке может быть строго доказана. Однако, ни общий вид многочленов наилучшего равномерного приближения, ни способы их построения, неизвестны. Имеются лишь методики построения многочленов наилучшего равномерного приближения для достаточно узкого класса функций и некоторые способы построения многочленов близких к многочленам наилучшего равномерного приближения.

Пример 2.5. Пусть для непрерывной функции на интервале требуется построить многочлен наилучшего равномерного приближения нулевой степени . Для того чтобы найти значение воспользуемся свойством непрерывной на ограниченном замкнутом интервале функции, согласно которому на этом интервале найдутся по крайней мере две точки, в которых функция принимает максимальное и минимальное значение. Введем обозначения:

, .

Тогда

,

при этом абсолютное отклонение определится по формуле

.

Пример 2.6. Пусть для непрерывной функции на интервале требуется построить многочлен наилучшего равномерного приближения степени . В силу определения наилучшего равномерного приближения многочлен должен быть наименее отклоняющимся от нуля на интервале . Но такой многочлен степени нам известен это многочлен Чебышева . Тогда из равенства

=

легко определить многочлен :

.

В частном случае при имеем:

.

Таким образом получаем, что наилучшим равномерным приближением для на интервале является многочлен третьей степени.

Сравним точность построенного многочлена наилучшего равномерного приближения с многочленом Лагранжа 3-ей степени, построенного по чебышевским узлам (2.36) (см. п. 2.9). Для нашего случая этот многочлен будет иметь вид:

.

На рис 2.2. приведен график ошибок аппроксимации

для многочлена наилучшего равномерного приближения (сплошная линия) и график ошибки аппроксимации многочленом Лагранжа

(пунктирная линия). Как видно из графиков точность аппроксимации на интервале с использованием многочлена наилучшего равномерного приближения выше и величина максимальной ошибки в 2 раза меньше чем при аппроксимации многочленом Лагранжа (максимальная ошибка достигается на концах интервала и равна 0,125, см. рис. 2.2).

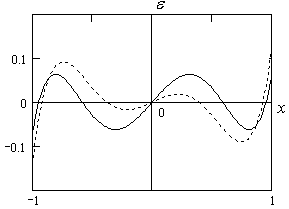
Рис. 2.2. Графики ошибок аппроксимации

2.10. Экономизация степенных рядов

В некоторых задачах достаточно просто получить аппроксимацию функции с помощью ряда Тейлора вида:

,

сходящегося при . Тогда может быть применен следующий метод построения аппроксимирующей функции:

1) подбирается значение , такое, чтобы многочлен

,

аппроксимировал функцию с погрешностью, не превышающую величину ;

2) степень многочлена понижается на единицу посредством замены на наилучшее равномерное приближение степени .

Выполнив эти два этапа, получим аппроксимирующий многочлен степени :

.

Погрешность аппроксимации функции определится на интервале оценкой

Такой подход позволяет осуществить экономизацию степенного ряда, не снижая значительно точность аппроксимации. Если полученная оценка позволяет дальнейшую экономизацию степенного ряда, можно попытаться понизить степень аппроксимирующего многочлена еще на единицу.

Экономизацию степенного ряда можно осуществлять также с помощью замены аппроксимирующего многочлена эквивалентным разложением по многочленам Чебышева . Для этого можно воспользоваться выражениями степеней через многочлены Чебышева:

, , ,

, ,

и т.д.

Отметим, для достижения одной и той же точности в отрезке разложения по многочленам Чебышева можно брать, как правило, меньшее число членов, чем в степенной аппроксимации.