8.4. Усилия при волочении труб

Определение усилий волочения Q_в непосредственно связано с выбором допустимых разовых деформаций и производительности волочильных станов.

Аналитические методы определения усилий волочения труб основаны на законах механики пластически деформируемого тела и условия пластичности. Согласно этим методам, совместно решаются дифференциальные уравнения равновесия сил, действующих на выделенный в очаге элементарный объем металла и уравнения пластичности для каждого выделенного элемента очага деформации. При этом применяют следующие допущения: не учитывают внеконтактную деформацию металла в местах перехода одного элемента очага деформации к другому; отсутствует неравномерность деформации по поперечному сечению стенки трубы; не учитываются внутренние потери (по С.И. Губкину); главные напряжения принимаются одинаковыми во всех точках на одной и той же поверхности.

Расчетное сопротивление деформации σ_sр по всей длине деформационной зоны принимается постоянным, равным его среднему значению:

σ_sр = (σ_в^о + σ_в^в)/2 (8.8а)

или

σ_sр = (σ_т^н + σ_т^в)/2, (8.8б)

где σ_в^о и σ_в^в – пределы прочности (временное сопротивление) металла трубы до и после волочения; σ_т^н и σ_т^в – истинные пределы текучести, определяемые с учетом неравномерности деформации по наружной и внутренней поверхности трубы.

На рис. 8.4 приведены кривые упрочнения, полученные Г.А. Савиным при безоправочном волочении углеродистых труб типоразмера D_т×S_т = 57,0×4,1 мм со скоростью 30 м/мин.

Усилие волочения, под действием которого труба протягивается через волоку, принято определять по напряжению волочения s_е:

Q_в = s_еF_тр , (8.9)

где F_тр – площадь поперечного сечения трубы после волочения.

Ниже приведены формулы расчета напряжений при безоправочном волочении труб.

1. Формула И.Л. Перлина

σ_е = 1,15 σ_т^ср[(а – 1) /а]•[1 – (D_т^ср / D_з^ср)²] + (D_т^ср / D_з^ср) (8.10)

где s_т^ср = (s₀ – s₁)/2 среднее значение предела текучести материала до и после деформации, или 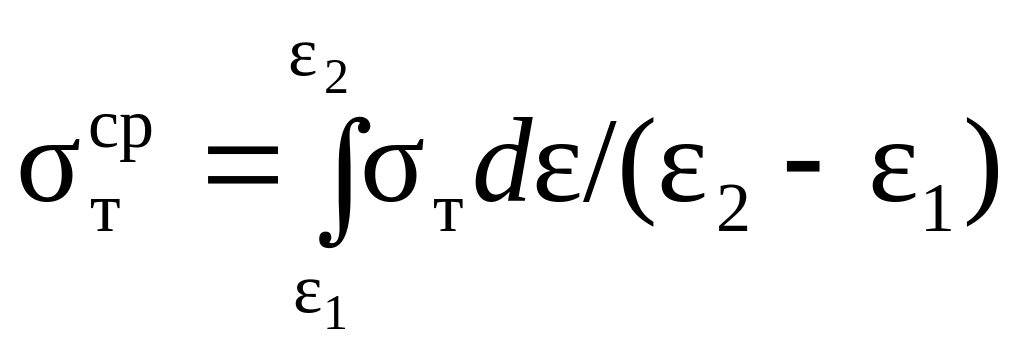. Зависимость s_т^ср = F(e) может быть получена методом регрессионного анализа на основании экспериментальных данных. Значение s_упр = 0,2s₀ – напряжение на границе упругой и пластической зон; s₀ – предел прочности исходного материала (заготовки);

;

f – коэффициент трения; a¢ – приведенный угол волоки;

tga¢ = ,

D_з, D_т – диаметры заготовки и трубы; D_з^ср, D_т^ср – средние диаметры заготовки и трубы (D_з^ср = d_з + S; D_т^ср = d_т + S_т); a – половина угла входного конуса волоки; l_п » 0,5S_т – длина калибрующего пояса волоки.

2. Формула Л.Е. Альшевского

, (8.11)

где  = (tg + f) / (1 – f tg) tg.

3. Формула Е. Зибеля

s_е = s_срln(F_з/F_т) (1 + 2f/sin2a), (8.12)

где F_з, F_т – площадь поперечного сечения заготовки и трубы.

В табл. 8.2 приведены результаты расчета напряжения безоправочного волочения по формулам разных авторов и для сопоставления экспериментальные данные НГТИ (бывш. ВНИТИ).

Таблица 8.2. Расчетные и экспериментальные напряжения при безоправочном волочении

Dт ´ Sт*, мм	sрасч, Н/мм2, по формулам			sэкспер, Н/мм2
	(8.10)	(8.11)	(8.12)
(47,0 ´ 6,0)/(42,0 ´ 6,0)	147	147,7	140	146
(42,0 ´ 2,6)/(34,0 ´ 2,6)	77	76,3	79,5	74
(40,0 ´ 1,9)/(35,0 ´1,9)	42	54,8	50,4	50
(38,0 ´ 1,7)/(30,0 ´ 1,7)	48	57,0	52	53
(34,0 ´ 2,7)/(27,0 ´ 2,7)	68	72,9	67,5	68
(32,0 ´ 3,9)/(26,0 ´ 3,9)	89	90	87,9	88

^* Числитель – до, знаменатель – после волочения.

4. Формула М.М. Бернштейна

s_е = 0,105 [1 – sin(a/2)] (1 + f) , (8.13)

где e = (D_з – D_т) / D_з.

Формула М.М. Бернштейна наиболее проста, но она эмпирическая, поэтому при учете влияния разных факторов процесса на напряжение волочения следует пользоваться формулами И.Л. Перлина и Л.Е. Альшевского.

Напряжение при волочении на неподвижной (короткой) оправке можно определить по следующим формулам.

1. Формула И.Л. Перлина

s_е = 1,15s²[1 + (tga¢)/(А₁f)] [1 – F_т/ + s^′(F_т/ , (8.14)

где s² – среднее значение предела текучести материала в зоне обжатия стенки: s² = (s_I + s_II)/2; здесь s_I – предел текучести материала в конце зоны осаждения; s_II – предел текучести материала в конце обжатия стенки; F₁ – площадь поперечного сечения трубы в конце зоны осаживания; s^′ – растягивающее осевое напряжение на границе зон обжатия и осаживания стенки, определяемое по формуле И.Л. Перлина для безоправочного волочения;

А₁ = 1 + d_т cosa¢/(d_т + S_з + S_т),

где d_т – внутренний диаметр трубы.

2. Формула Л.Е. Альшевского

s_е = [1/(w₁ – 1)] {(F_т/F₁)^ω–1е^–2ƒl/S[ω₁(σ_е1 - σ″) – σ_е1] + σ″(е^–2ƒl/S + ω₁ – 1)}, (8.15)

где w₁ = , здесь b = d_т/D_т; s_I – растягивающее осевое напряжение на границе зон: s_I = [s¢w/(w – 1)][1 – (D_I^ср/D_з^ср)^w–1],

s¢ = (s₀ + s_I)/2 – среднее значение предела текучести материала в зоне осаживания.

3. Формула В.А. Кочкина

s_е = s_срln(F_з/F_т)(1 + f/sinacosa + f/tga). (8.16)

При волочении на короткой неподвижной оправке на стержень действует растягивающее усилие, величину которого можно определить по формуле И.Л. Перлина:

Q₀ = 0,5(s_I – s¢ + s_II – s) pd_тl_оп f, (8.17)

где l_оп – длина оправки в очаге деформации:

l_оп = (S_з – S_т)/tga + l_п,

или по формуле Л.Е. Альшевского

Q₀ = 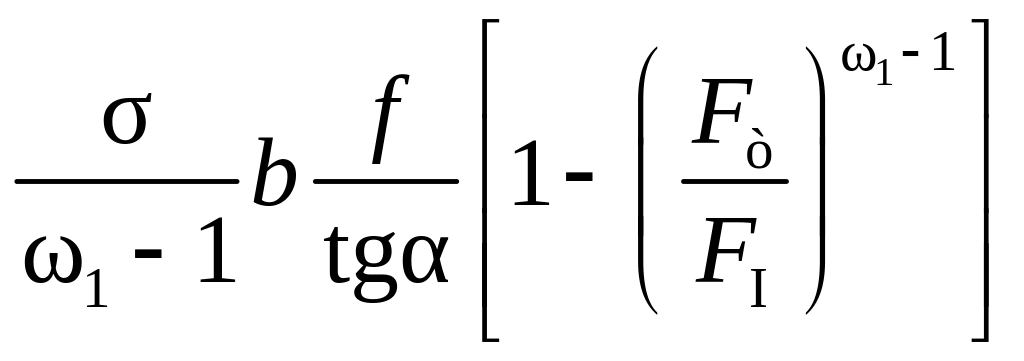F_т. (8.18)

Напряжение при волочении на подвижной длинной оправке определяют по следующим формулам.

Формула И.Л. Перлина

s_е = 1,1s²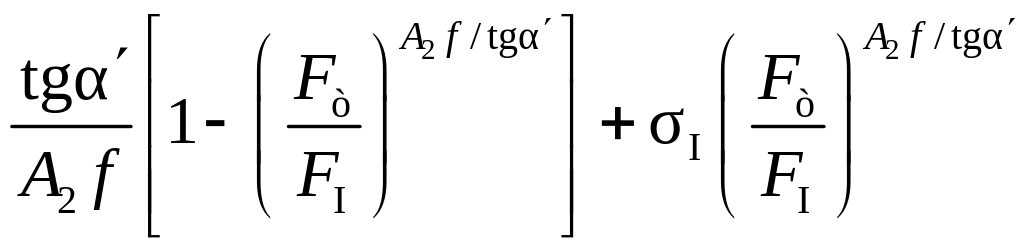 , (8.19)

где А₂ = 1 – d_тcosa¢/(d_т + S_з + S_т).

2. Формула Л.Е. Альшевского

s = [1/(w₂ – 1)] 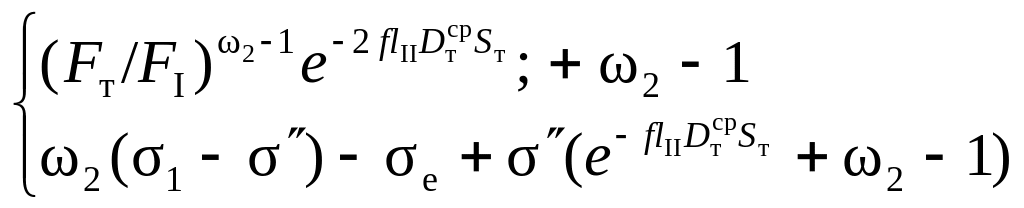. (8.20)

Усилие на оправке при волочении с трубой (по Л.Е. Альшевскому)

Q₀ = [1 – (F_т/ ]F_т. (8.21)

С учетом усилия на оправке общее усилие волочения

Q = sF_т + Q₀. (8.22)

3.Формула М.М.Бернштейна

s = 0,145 [1 – sin(a/2)] (1 + f) . (8.23)

При расчетах напряжений волочения можно принимать коэффициент трения для углеродистой и низколегированной сталей f = 0,11÷0,13.

Для определения тягового усилия волочения при практических расчетах можно пользоваться упрощенными формулами П.Т. Емельяненко и Л.Е. Альшевского:

при волочении без оправки:

Q = 1,1bs^срЕАF_I; (8.24)

при волочении на неподвижной оправке

Q = 1,05s_срE₁АF_т; (8.25)

при волочении на подвижной оправке

Q = 1,75s_срE₂АF_т. (8.26)

Здесь b = 1,05¸1,15 – коэффициент, учитывающий влияние среднего главного напряжения (для тонкостенных труб b = 1,0); s^ср – среднее значение предела текучести материала трубы; А = (F_з – F_т)/F_з; ;  + + af/tg; – af/tg; (8.27)

a – угол наклона стенки волоки к оси волочения; f – коэффициент трения между оправкой, волокой и трубой; а – отношение радиуса оправки к среднему конечному радиусу трубы.

На усилие волочения влияют механические свойства обрабатываемого материала, степень деформации, условия внешнего трения, геометрия очага деформации и другие факторы.

С увеличением временного сопротивления и степени деформации увеличивается усилие волочения. Хорошая технологическая смазка способствует резкому снижению усилий волочения. Большое влияние на усилие волочения оказывает угол конусности волоки α и длина цилиндрического пояска. С увеличением угла  уменьшаются протяженность очага деформации, сила нормального давления и горизонтальная составляющая сил трения, но одновременно увеличивается горизонтальная составляющая силы нормального давления. В зависимости от степени влияния того или иного фактора усилие волочения может увеличиваться или уменьшаться. При малых значениях угла  усилие волочения с ростом  снижается, а при больших значениях  – возрастает. И.Л. Перлин показал, что для каждой степени деформации за проход существует оптимальное значение угла , при котором усилие волочения минимально. Оптимальный угол a увеличивается с повышением обжатия и коэффициента вытяжки. На основании опытных данных установлено, что оптимальный угол наклона конусной части канала волоки  = 0,210÷0,245 рад, при f = 0,10¸0,15.

При профилировании трубы напряжение волочения рассчитывают по формуле А.И. Дорохова (см. Дорохов А.И. Осевые напряжения при волочении фасонных труб без оправки. Тр. УкрНИТИ. Вып. 1. – М.: Металлургиздат, 1959).