3.3. Энергосиловые параметры при холодной периодической прокатке труб

В процессе холодной периодической прокатки каждое сечение заготовки деформируется в постоянно изменяющемся мгновенном очаге как при прямом, так и при обратном ходе клети. На рис. 3.8 показана схема действия сил в мгновенном очаге деформации при холодной прокатке на стане ХПТ.

С достаточной степенью точности для расчетов принимают точку приложения сил нормального давления и касательных сил трения по середине дуги касания металла с валком (см. рис. 3.8).

Величину вертикальной составляющей усилия металла на валок Р_в при прямом и обратном ходе клети стана ХПТ определяют по формуле:

Р_в = рF_кон. (3.14)

Для определения средних нормальных контактных напряжений Ю.Ф. Шевакиным предложены эмпирические формулы:

для прямого хода клети

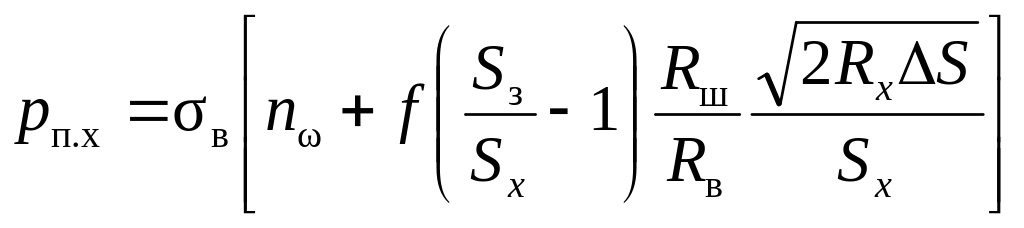, (3.15)

для обратного хода клети

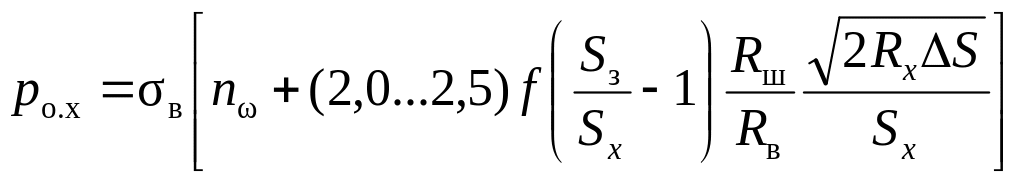, (3.16)

где _в – временное сопротивление прокатываемого металла при данной степени деформации; n_ – коэффициент, учитывающий влияние среднего главного напряжения; f – коэффициент внешнего трения (для стали f = 0,08…0,12); S_з – толщина стенки заготовки, мм; R_ш – радиус ведущей валковой шестерни, мм.

Площадь контактной поверхности соприкосновения металла с валком можно представить состоящей из поверхности соприкосновения в зоне обжатия стенки (см. рис. 3.6, а) и в зоне редуцирования (см. рис. 3.6, б)

(3.17)

Весьма простые, но сравнительно точные формулы для определения площади контактной поверхности рекомендует Ю.Ф. Шевакин:

(3.18)

(3.19)

где – коэффициент формы контактной поверхности; – ширина и диаметр ручья в рассматриваемом сечении; – полное обжатие в очаге деформации; – радиус валка по вершине калибра: ; – обжатие по толщине стенки в очаге деформации.

Для определения горизонтальной проекции контактной поверхности при прямом или обратном ходе клети следует вместо подставлять соответственно или . При учете упругого сплющивания валков горизонтальную проекцию контактной поверхности с учетом упругого сплющивания Ю.Ф. Шевакиным рекомендуется рассчитывать по формуле:

, (3.20)

где _в – временное сопротивление материала трубы при данной степени деформации.

Для определения усилия металла на валки необходимо рассчитать калибровку ручья и определить давление в нескольких контрольных сечениях по длине ручья для того, чтобы установилось наибольшее усилие. Избежать предварительного расчета калибровки, мгновенных обжатий и др. параметров можно, воспользовавшись формулой Ю.Ф. Шевакина для определения полного усилия металла на валки:

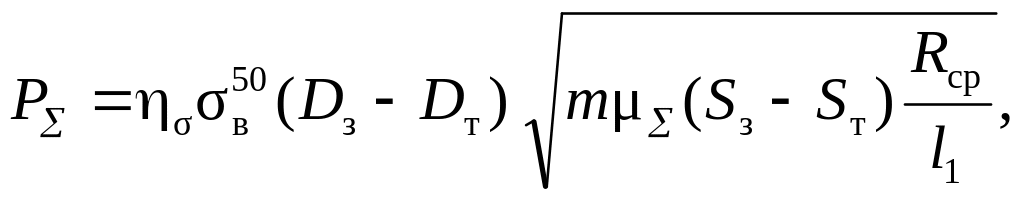(3.21)

где _ = 1,42 для стали, сплавов титана и 1,10–1,17 – для сплавов на основе меди и алюминия – коэффициент, зависящий от характера упрочнения металла; – временное сопротивление материала при 50%-ной деформации; – средний радиус обжимной зоны ручья: – длина рабочей части ручья без калибрующего участка.

Осевые усилия, действующие на заготовку. При холодной прокатке труб на заготовку со стороны валков приложены значительные осевые усилия разного знака. Это является результатом отсутствия равновесия горизонтальных составляющих усилий, действующих в очаге деформации. Большое влияние на величину и направление тангенциальных сил оказывают скоростные условия, которые при холодной прокатке весьма сложны.

Ю.Ф. Шевакин рекомендует определять осевые усилия при холодной периодической прокатке по следующим формулам.

При прямом ходе клети, если зона отставания мала по сравнению с зоной опережения, т. е. ω_х < _о (см. рис. 3.8):

. (3.22)

Если , то:

(3.23)

При обратном ходе клети, если R_ш > R_обж, то

_(3.24)

если R_ш < R_обж ,то:

_(3.25)

где Р_Σпр – среднее полное усилие на валки при прямом ходе клети; Р_Σоб – среднее полное усилие при обратном ходе клети; Р_Σоб = (0,7…0,9)P_Σпр; R_ш – радиус ведущей валковой шестерни; R_обж – радиус валка в обжимной части ручья для рассматриваемого сечения; f – коэффициент внешнего трения; α_В – угол выпуска ручья; – центральный угол, определяющий протяженность очага деформации в области обжатия стенки; – угол, ограничивающий зону отставания металла относительно поверхности валка; K_α – коэффициент, характеризующий степень участия выпуска ручья в деформации металла и зависящий от характеристики поворотно-подающего механизма:

Участок ручья . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	Начало*	Середина*	Конец*
Коэффициент K при
раздельных повороте и подаче трубы . . . . .	0,50 / 1,00*	0,25 / 0,85	0 / 0,76
совмещенных повороте и подаче трубы . . . .	0,25 / 0,90	0,10 / 0,70	0 / 0,50
двойном повороте трубы . . . . . . . . . . . . . . . .	0,75 / 0,75	0,50 / 0,60	0,25 / 0,50

* В числителе – прямой ход клети, в знаменателе – обратный.

Осевое усилие в значительной степени определяется усилием металла на валки (рис. 3.9, а) и влияющими на него параметрами. Однако наиболее влияет на осевое усилие радиус начальной окружности ведущей валковой шестерни, от которого зависят величина и знак осевого усилия (рис. 3.9, б).

Осевое усилие, действующее на заготовку, достигает максимума к концу хода клети. При больших значениях сжимающего осевого усилия теряется устойчивость трубы в продольном направлении, а растягивающие осевые усилия вызывают продольное смещение заготовки. Наиболее эффективное средство снижения осевых усилий – изменение радиуса начальной окружности ведущей валковой шестерни.

Момент прокатки, необходимый для деформации металла, без учета потерь на трение и динамических потерь, расходуется на преодоление моментов от вертикальной составляющей полного и осевого усилий.

Полный момент прокатки (для двух валков) зависит от направления хода клети.

При прямом ходе клети:

(3.26)

Если осевое усилие при прямом ходе клети сжимающее (направлено против движения клети), то момент его осевого усилия суммируется с моментом от сил давления, а если осевое усилие растягивающее, то полный момент представляет разность моментов сил давления и осевых.

При обратном ходе клети:

(3.27)

Если осевое усилие при обратном ходе клети сжимающее (направлено по направлению движения клети), то полный момент представляет разность моментов от R_Σоб и Q_Σоб, а если осевое усилие растягивающее (направлено против движения клети), то полный момент равен сумме моментов этих сил.

Определение моментов значительно упрощается с использованием величины усредненного полного давления:

при прямом ходе

(3.28)

при обратном ходе:

(3.29)

где R_расч = R_б – [(r_з–r_т)/4] – расчетный радиус валка; n_Q = 0,08÷0,1 – коэффициент, зависящий от скоростных условий процесса; ΔS_ср – среднее обжатие за цикл: ΔS_ср = (S₃–S_T)/n_д, n_д = 3l_обж / [m (1+2μ_Σ)] – коэффициент дробности деформации: l_обж – длина обжимной части ручья.