Розділ 4. Моделювання оптимальної ціни

У курсовому проекті використовується цінова стратегія, що базується на попиті, із врахуванням впливу інших методичних підходів, оскільки вони взаємопов’язані. Використання обраної методики передбачає, що попит може бути визначений із значною точністю. Отже, фірма “Touch” використовує метод максимізації поточного прибутку, який належить до моделі ціноутворення, що базується на ринковому попиті на товар. Оскільки із законом попиту зниження ціни на товар збільшує попит на нього (обсяг його збуту), і навпаки, фірма хоче знайти таку точку ціни на кривій попиту, яка забезпечить максимальний прибуток у найближчій перспективі.

4.1Визначення взаємозв’язку між ціною і попитом

Для оцінки взаємозв’язку між ціною і попитом на свій товар фірма протягом декількох місяців проводила пробний маркетинг товару при різних значеннях ціни.

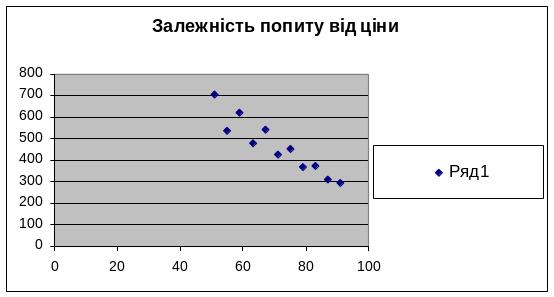
Рис 1. Кореляційне поле точок

Складаємо рівняння регресії, що встановлює зв’язок між параметрами: ціною та обсягом збуту. Оскільки зв’язок між ними близький до лінійного, то рівняння регресії буде мати вигляд:

N = b­­_{0 ­}+ b­₁ × Ц ,

де N – теоретичне значення обсягу збуту при відповідній ціні.

Для обчислення b­­_0­ та b­₁ розв’яжемо систему нормальних рівнянь:

_{m m}

∑ n_i = m × b₀ + b₁ ∑ Ц_і

^{i =1 i =1}

_{m m m}

∑ n_i × Ц_і = b₀ ∑ Ц_і + b₁ ∑ Ц_і²

^{i =1 i = 1 i = 1}

де m – кількість замірів у проведеному дослідженні.

Щоб розвязати дану систему помножимо перше рівняння на:

_m

∑ Ц_і

^{i = 1}

m

та віднімемо друге рівняння від першого.

Таблиця 1. Проміжні дані для розрахунку

Заміри	Ці	ni	Ці*ni	Ці2	ni2	Ni	Ni - nc.	(Ni - nc.)2
1	91	293	26663	8281	85849	458,3513	-6,19419	38,36803
2	87	309	26883	7569	95481	459,5901	-4,95535	24,55554
3	83	375	31125	6889	140625	460,8289	-3,71652	13,81249
4	79	366	28914	6241	133956	462,0678	-2,47768	6,138885
5	75	458	34350	5625	209764	463,3066	-1,23884	1,534721
6	71	424	30104	5041	179776	464,5455	0	0
7	67	540	36180	4489	291600	465,7843	1,23884	1,534721
8	63	481	30303	3969	231361	467,0231	2,47768	6,138885
9	59	620	36580	3481	384400	468,262	3,71652	13,81249
10	55	539	29645	3025	290521	469,5008	4,95535	24,55554
11	51	705	35955	2601	497025	470,7396	6,19419	38,36803
12	47	596	28012	2209	355216	471,9785	7,43303	55,24997
Σ	828	5706	374714	59420	2895574	5581,978	—	224,0693

Визначаємо коефіцієнти b­­_0­

5706= 12× b­­_0­ + b­₁ × 828

374714= b­­_0­ × 828 + b­₁× 59420

Провівши відповідні розрахунки, отримаємо:

b­₁ = -0,30971

b­­₀ = 486,534841

Обчислені дані дають змогу скласти рівняння регресії, що матиме наступний вигляд:

N =486,534841–0,30971× Ц

Покажемо залежність обсягу збуту (N) від ціни (Ц) на графіку. Графік функції N = f(Ц) наведений на рис.2.

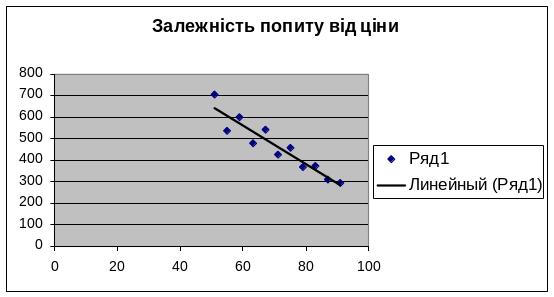
Рис.2.Залежністі попиту від ціни

Визначимо щільність зв’язку між цими величинами, шляхом обчислення коефіцієнта детермінації, що характеризує ту частину варіації результативної ознаки “n”, яка відповідає лінійному рівнянню регресії.

σ² N

R ² = ,

σ² n

m

де σ² N – факторна дисперсія, σ² N = ∑ (N_i –n_с.)² / m ;

^{i = 1}

де σ²_n – загальна дисперсія, σ²_n = ∑ n_i² / m - ∑n_i / m

^{і =1 і = 1}

σ² N = 224,0693/ 12 = 18,67

σ²_n = 2895574 / 12 – (5706 / 12) = 240822,5

R² = 18,67 / 240822,5= = 0,001203399

Оскільки, R² = 0,001203399, то можна зробити висновок про те, що існує досить слабкий зв'язок між попитом і ціною на товар.