Chapter 6
Statistical quality control
6.1. Introduction
In manufacturing process, there is always some variation in the items manufactured. For example, even though a machine is designed to cut a piece of pipe a certain length, the lengths of the pipes cut will not all be exactly equal. There are two causes of variation: normal or chance of variation; and variation that is due to human or mechanical reasons in the manufacturing process. If the variation is due to human or mechanical reasons in the process, this causes defective parts, it must be detected at an early stage and corrected.
A real life example concerns the weights of canned food. In this case, a food producer wishes to provide assurance that the minimum weight of its canned product is being met. Food producers have a tendency to fill cans with more food than the can’s label indicates, out of fear of being caught with under weight cans by the state inspectors.
The question is, “how does one determine (with the variability in the filling process) with assurance that the minimum weight of all cans is being achieved and at the same time, not lose money by overfilling each can? This chapter will explain a technique called statistical quality control, which can be used to answer this question.
6.2. Variation
One of the fundamental principles of the statistical thinking is that variation exists in all process. It is important to understand variation in order to predict the future performance of the process. There are two causes of variation:
common causes
assignable causes
Common causes of variation (also called uncontrollable causes) are those causes that are random in occurrence and are happens during all process. Management, (not workers), are responsible for these causes.
Assignable causes of variation (also called special cases) are the results of external sources, that is, sources that are outside of the system. These causes can and must be detected, and corrective actions must be taken to remove them from the process. Not taking actions will increase variation and lower the quality.
Definition:
A production process is called stable (in-control) if all assignable causes are removed; thus, variation results only from common causes.
6.3. Control charts
Figure 6.1 illustrates the general format of a process control chart. The upper and lower control limits define the normal operating region for the process.
The horizontal axis reflects the passage of time, or order of production. The vertical axis corresponds to the variable of interest. There are number of different types of process control charts. We will consider the most commonly used process control charts
chart
chart
chart
chart
6.3.1 Control charts for means and standard deviations
Let us consider a production process that yields an output whose characteristic of interest can be measured on a continuum. It is necessary to set up a quality control scheme for that process. It can be done by taking, over time, a sequence of small samples of output. Often samples of four or five are taken. The frequency of sample observations depends on the characteristics of production process. Management is often interested in both average performance of production process and the variability in process. Sample means and standard deviations are used to track process performance. Three measures used in the development of control charts for means and standard deviations. They are: overall mean, the average sample standard deviation, and the process standard deviation.
Assume
that a sequence of K
samples, each of n
observations, is selected over time from the production process. The
sample means denoted
for
can
be graphed on an
chart.
The average
of these sample means is
called the overall
mean
of all the sample observations
The
sample standard deviations denoted
for
can
be graphed on an
chart.
The average
sample standard deviation
is
The
process
standard deviation,
is the standard deviation of the population from which the samples
were drawn, and it must be estimated from the sample data.
Since the sample standard deviation is based on n observations, it can be shown that
where
is
the number that can be computed as a function of the sample size n.
It follows that
and hence that an unbiased estimate of the process standard deviation is given by
The value of -control chart factor, can be found in Table 6.1. Table 6.1 lists values of , corresponding sample sizes from two to ten. It also contains factors for other control charts that will be discussed throughout this chapter.
Table6.1 Factors for control charts
-
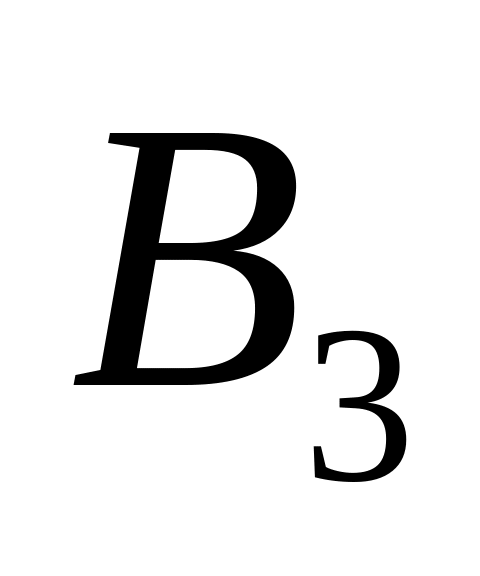
2
3
4
5
6
7
8
9
10
0.7879
0.8862
0.9213
0.9400
0.9515
0.9594
0.9650
0.9690
0.9727
2.659
1.954
1.628
1.427
1.287
1.182
1.099
1.032
0.975
0
0
0
0
0.030
0.118
0.185
0.239
0.284
3.267
2.568
2.266
2.089
1.970
1.882
1.815
1.761
1.716
To
determine control limits for
-charts, we assume that the process has been operating at a constant
level of performance over the whole observation period and, assume
that all sample observations have been drawn from the same normal
distribution.
The sampling distribution is centered on the overall mean, and the value of the overall mean determines the central line, called center line. Then, if three-standard error limits are to be used, the control limits are
where
Control chart for means
The chart is a time plot of the sequence of sample means.
The center line is
In addition, there are three-standard error control limits.
The lower control limit is
The upper control limit is
where
the values of
are
given in Table 6.1.
Example:
The accompanying table shows sample means and sample standard deviations for a sequence of 10 samples of seven observations on a quality characteristic of a product
-
Sample
1
2
3
4
5
6
7
8
9
10
145.2
139.2
146.3
138.2
141.2
144.3
140.1
139.9
145.5
143.3
2.3
3.1
2.1
1.9
2.4
2.2
3.1
2.3
2.7
2.8
a) Find the center line and lower and upper control limits for an chart.
b) Draw the chart.
Solution:
a) First of all, let us find overall mean and average of the sample standard deviations are
The
sample size is seven. So from table 6.1 we obtain
.
The central line is
The lower control limit is
The upper control limit is
b) Each of the individual sample means are plotted on chart in Figure 6.1. Three of the values fall out side of the control limits and there seems a great cause for concern. It is necessary to take action to correct the production process.
`
`
`
Control chart for standard deviations
The chart is a time plot of the sequence of sample standard deviations.
The center line is
In addition, there are three-standard error control limits.
The lower control limit is
The upper control limit is
where
the values of
and
are
given in Table 6.1.
Example: Refer to the data of example above.
a) Find the center line and lower and upper control limits for an chart.
b) Draw the chart and discuss its features
Solution:
a)
The
sample size is seven. So from table 6 of the appendix we obtain
and
The center line is
In addition, there are three-standard error control limits.
The lower control limit is
The upper control limit is
b)
We plot each of the individual standard deviations on a control chart
with center line
,
lower control limit
,
and upper control limit,
.
The s-chart
will look like Figure 6.3.
The observed sample standard deviations are fall between lower and upper control limits. From this point of view, the process is under control. But since, the mean production process is out of control, the general production process must be corrected.