Г.А. Тихановская, Л.М. Воропай

ХИМИЯ ВОДЫ

задачи и упражнения

Учебное пособие

Вологда

2010

Федеральное агентство по образованию

Вологодский государственный технический университет

Г.А. Тихановская, Л.М. Воропай

ХИМИЯ ВОДЫ

задачи и упражнения

Учебное пособие

Утверждено редакционно – издательским советом ВоГТУ

в качестве учебного пособия

Вологда

2010

УДК 543.39 (075)

ББК 38.761я73+26.22

Рецензенты:

кандидат химических наук, доцент ВГМХА Т.Л. Бланк;

главный специалист ООО «Александра Плюс» М.А. Тихонов.

.

Тихановская, Г.А., Воропай Л.М.

Химия воды. Задачи и упражнения: учеб. пособие / Г.А. Тихановская, Л.М. Воропай. – Вологда: ВоГТУ, 2010. - с.

Учебное пособие (задачи и упражнения) по курсу «Химия воды и микробиология» для студентов специальности 270112 «Водоснабжение и водоотведение» является третьей частью курса, составлено на основании требований Государственного образовательного стандарта высшего и профессионального образования с учетом требований к минимуму содержания и уровню подготовки инженеров по специальности 270112.

В пособие включены задания, предусмотренные программой курса «Химия воды и микробиология», приведены способы решения типовых задач и краткие теоретические предпосылки.

В пособие входит глоссарий и таблицы по основным параметрам, используемым при характеристике природных и сточных вод, а также расчеты, применяемые в химических технологиях обработки воды.

Пособие может быть использовано для студентов дневного и заочного отделения специальности 270112, при выполнении контрольных и расчетно – графических работ.

УДК 543.39 (075)

ББК 38.76я73+26.22

Вологодский государственный

технический университет, 2010

Тихановская Г.А., Воропай Л.М., 2010

Предисловие

Задачи и упражнения по химии воды можно рассматривать как третью часть спецкурса «Химия воды и микробиология». Основное содержание составляет материал, предусмотренный программой курса. Подробно рассматриваются общетеоретические основы курса, без знания которых невозможно осуществление каких – либо химических расчетов. Разделы – «Показатели качества воды» и «Физико – химические основы очистки природных вод» включают способы и методы расчета качества реагентов и оценки качества воды для отдельных видов водопользования.

В задачнике приведены решения типовых задач и даны задания для самопроверки усвоения знаний. Этот материал может быть использован при выполнении контрольных работ, студентами заочного обучения. Приведенный в пособии глоссарий помогает работать с материалом при изучении отдельных разделов курса.

В пособие включены формулы и зависимости, используемые при приготовлении растворов, формулы для пересчета концентраций растворов, расчет концентраций ионов Н⁺, ОН^- и рН растворов различных соединений.

Отдельным разделом идут примеры решения задач на расчеты закономерностей процессов, происходящие в природных водах различного происхождения.

Общетеоретические основы курса

1. Фазовые равновесия. Диаграмма состояния воды

Основной закон фазового равновесия часто называют правилом фаз. Правило фаз выражает количественную связь между числом фаз, существующих в равновесной системе при данных условиях, составом системы и числом независимых переменных, минимально необходимых для определения ее состояния.

Формулировка правила фаз (Гиббс): в равновесной системе сумма чисел фаз и степеней свободы равна числу компонентов, увеличенному на два:

Ф + С = К + 2, где

Ф – число фаз,

С - число степеней свободы,

К – число компонентов.

Фаза – однородная внутри себя часть неоднородной системы и отделимая от нее механическим путем. Следовательно, различные фазы гетерогенной системы отделены друг от друга поверхностями раздела. Фаза хотя и однородна, но она не обязательно должна состоять из молекул одного и того же вида. Например, раствор сахара в воде, спирта в воде, смесь газов, твердый однородный сплав представляет собой одну фазу. Если же две жидкости ограниченно растворимы друг в друге или вообще нерастворимы, то они образуют две фазы, например вода и эфир или эмульсия бензола в воде.

Химически индивидуальные вещества, образующие данную систему и способные существовать самостоятельно, называются составными частями системы. Например, раствор хлорида натрия в воде состоит из двух составных частей: молекул воды и молекул хлорида натрия. Ионы электролита (Na⁺, Cl^-) не считаются составными частями системы, так как не способны существовать изолированно от системы.

Вещества, концентрацию (давление) которых в равновесной системы можно задавать, называются независимыми составными частями или ее компонентами. Вещества, концентрации (давления) которых в равновесной системе устанавливаются в результате химических реакций без вмешательства экспериментатора, называются независимыми составными частями системы. Например, при температуре 2000 ⁰С существует равновесная химическая система:

2Н₂О ↔ 2Н₂ + О₂

Если мы заранее зададим парциальные давления водорода и кислорода, то при данных условиях само собой установится парциальное давление паров воды в соответствии с законом действующих масс. Если же заранее установить парциальное давление паров воды и водорода, то само собой установится парциальное давление кислорода. Таким образом, составных частей в этой системе три, а компонентов – два.

Число степеней свободы определяет собой вариантность (изменчивость) системы. Если С = с, то система моновариантна, если С = 2, то система бивариантна. Если гетерогенная система не имеет никакой степени свободы (С = 0), то ее называют безвариантной (инвариантной, нонвариантной).

По количеству компонентов системы делят на одинарные (однокомпонентные), двойные (двухкомпонентные), тройные (трехкомпонентные) и т.д.

Пример 1. Определение числа степеней свободы в гетерогенной равновесной системе. Найдите число сте­пеней свободы в точке М на диаграмме состояния воды.

Решение. Число степеней свободы (С) в равновесной гетерогенной системе подсчитывают с помощью уравнения Гиббса (уравнение правила фаз) : С=К- Ф+2 , где К- число независимых компонентов системы; Ф-число фаз в системе.

Данная система однокомпо­нентная:

В Е фаза системы ‑ это вода в различных

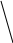агрегатных состояниях (пар, жидкость, лед)

вода С К=I. Точка М находится на кривой ОС,

. М отвечающей равновесию между двумя лед фазами: жидкость и пар, т.е в точке М

. О число фаз Ф=2. Число степеней свободы

в точке М равно С=I-2+2=I. В точке

Д М система имеет одну степень свободы:

А пар это означает, что до известного предела

можно изменять или температуру, или

давление и это не вызывает изменения числа и вида фаз системы.

Пример 2. Определить число степеней свободы в системе частично замерзшей воды.

Решение. В системе существует равновесие: лед↔ вода↔ пар, поэтому система имеет 3 фазы и одну составную часть. Так как эта система физическая, то число составных частей равно числу компонентов, то есть система однокомпонентна. Отсюда по уравнению Ф+С = К+2 находим С:

С = 1+2-3 =0

Система безвариантна. Это значит, что такая система может существовать только при строго определенных условиях (t = 0,01⁰С и р = 6,1 гПа).