Разложение вектора в ортогональном базисе.

Рассмотрим базис в пространстве Rn, в котором каждый вектор ортогонален остальным векторам базиса.

E1,e2,…en (ei,ej)=0, i<>j; I,j=1,2…n

Базисы такого вида удобны прежде всего тем, что координаты разложения произвольного вектора определяются весьма просто, без применения трудоемких вычислений.

Действительно, пусть требуется найти разложение произвольного вектора в ортогональном базисе e1-en. Составим разложение этого вектора с неизвестными координатами разложения в данном базисе.

b=α1e1+ α2e2+…+ αnen

умножим скалярно обе части этого равенства на вектор е1. Получим: (b,e1)= α1(e1,e1)+…+ αn(en,en)

(b,e1)= α1|e1|²

α1=

(b,e2)= α2(e2,e2)

α2=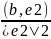

αi=

отметим особо частный случай ортогонального базиса, когда все базисные векторы имеют единичную длину, т.е. |ei|=1 или нормированы по своей длине.

E=(e1,e2,… en)

Eнорм=(

|eнорм|= =

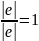
В таком случае базис называется ортонормированным. (ортогональный, |e_i| =1). Координаты разложения вектора в ортонормированном базисе имеют более простой вид. α_i=(b,e_i).

n-мерное векторное пространство Rⁿ называется Эвклидовым пространством, если в нем определяется скалярное произведение.

Верна следующая теорема: во всяком n-мерном эвклидовом пространстве существует ортонормированный базис.

(1,0,…0)(010,,,0),….(000,,,1) – ортонормированный базис.

Разложение вектора по ортонормированному базису в геометрическом пространстве.

Имеет место следующая теорема: любой геометрический вектор а может быть единственным образом разложен по базису ijk, т.е. представлен в виде а=xi+yj+zk, где x,y,z – координаты вектора а.

Переход к новому базису. Пусть в n-мерном пространстве имеются два базиса – старый и новый.

E1…en – старый базис e1*, e2*, … en* -новый базис.

К аждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса, т.е. записать, что (1)

e1*=a₁₁e1+a₁₂e2+…+a_1ne_n

E2*=a21e1+a22e2+…+a2n2n

En*=a_n1e1+a_n2e2+…+a_nnen

Полученная система означает, что переход от старого базиса e1…en к новому базису e1*…en* задается матрицей А=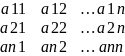

Матрица невырожденная, т.к. в противном случае ее строки (следовательно, и базисные векторы), обратный переход от нового базиса к старому осуществляется с помощью обратной марицы А^-1. Найдем зависимость между координатами вектора в разных базисах.

Пусть рассматриваемый вектор x имеет координаты x=(x1,x2…xn) в старом базисе, в новом – x=(x1*, x2*… xn*).

(2) Разложение вектора x через новый базис. X=x1*e1*+x2*e2*+…+xn*en*=x₁e1_x2e2+…+x_ne_n.

П одставляя значения e1 … en в левую часть равенства (2), получим после преобразований такую систему: x₁=a₁₁x₁*+a₂₁x₂*+…+a_n1x_n*

Xn=a_n1x₁*+a_2nx₂*+…+a_nnx_n*

X=A^Tx*

X*=(A^-1T)x

B=(4,-4,5) e1,e2,e3

векторы a1,a2,a3 образуют новый базис.

A1=(1,1,0) a2=(1,-1,1) a3=(-3, 5,-6)

Выразим связь между базисами.

A1=e1+1*e2+0*e3

A2=1*e1-1*e2+1*e3

A3=-3*e1+5*e2-6*e3

A=

A^-1=1/4

A^-1T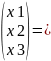=1/4

1/4

B=0,5a1+2a2-0,5a3

16.11.12 Ортогонализация системы векторов

Пусть имеется система векторов: A₁,A₂…A_m+1, надо преобразовать эту систему в систему ортогональных векторов.

(B_i,B_j)=0. B₁, B₂… B_m+1 – попарно ортогональные.

Схема процесса ортогонализации:

1. Процесс ортогонализации осуществляется по следующим формулам:

   1. B1=A1

   2. B2=A2 -

   3. B3=A3 -

   4. …

   5. B_m+1=A_m+1 –

Пример:

А1= (0 2), А2=(1 1).

B1=(0 2)

B2=(1 1) –

(B1,B2)= 0*1+2*0=0 – вектора ортогональные

Р ешение примеров: пример1.

A=(1,-2,2)

B=(-1, 0, -1)

C=(5,-3,-7)

B1=A1

B2=A2- (-1.0.-1)+1/3*(1.-2.2)=(-1.0.-1)+(1/3.-2/3.2/3)=(-2/3.-2/3.-1/3)

(B1,A2)=(1,-2,2)*(-1,0,-1)=-1+0-2=-3

B3=A3- =(5.-3.-7) +1/3*(1.-2.2)-1(-2/3.-2/3.-1/3)=(6.-3.-6)

(B1,A3)=(A1,A3)=1*5+6-14=-3

(B2,A3)=-10/3+2+7/3=1

4/9+4/9+1/9=1

B1=(1.-2.2)

B2=(-2/3.-2/3.-1/3)

B3=(6.-3.-6)

( B1,B2)=-2/3+4/3-2.3=0

(B1,B3)=6+6-12=0

(B2,B3)=-4+2+2=0

Векторы ортогональны.

Теперь нормируем. Каждую координату делим на длину.

| C1|=

|C2|= =1

| C3|=

Ортонормированный базис

Пример2.

A1(1.2.2.-1)

A2(1.1.-5.3)

A3 (3.2.8.-7)

B1=A1=(1.2.2.-1)

B2=A2-

B3=A3- 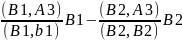=(3,2,8,-7)+3*(1.2.2.-1)+(2.3.-3.2)=(3.2.8.-7)+(3.6.6.-3)+(2.3.-3.2)=(2,-1,-1,-2) ошибка в подсчетах

(B1,B2)=2+6-6-2=0

(B1,B3)=2-2-2+2=0

(B2,B3)=4-3+3-4=0

Нормируем вектора. Разделим каждый вектор на его длину.

|B1|=sqr(1+4+4+1)=sqr(10)

C1=

C2= )

C3=(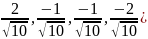

Ортонормированный базис.

Пусть b=(3.2.1.1)

b= λ1C1+ λ2C2+ λ3C3

λ1=(b,C1)=

λ2=(b,C2)=

λ3=(b,C3)=

Где-то ошибка, наверное в С2.