Результаты победителей олимпийских игр в беге на 200 м,

мужчины, золотые медалисты

Год	Фамилия	Страна	Время, в сек
1900	В. Тьюксберри	США	22,2
1904	А. Хан	США	21,6
1908	Р. Керр	Канада	22,6
1912	Р. Крейг	США	21,7
1920	А. Вудринг	США	22,0
1924	Дж. Шольц	США	21,6
1928	П. Вильямс	Канада	21,8
1932	Е. Толан	США	21,2
1936	Дж. Оуэнс	США	20,7
1948	М. Раттен	США	21,1
1952	А. Стансфилд	США	20,7
1956	Р. Марроу	США	20,6
1960	Р. Беррути	Италия	20,5
1964	Х. Кэрр	США	20,3
1968	Т. Смит	США	19,83
1972	В. Борзов	СССР	20,00
1976	Д. Кварри	Ямайка	20,23
1980	П. Меннеа	Италия	20,19
1984	К. Льюис	США	19,80
1988	Дж. Делоа	США	19,75
1992	М. Марш	США	20,01
1996	М. Джонсон	США	19,32
2000	К. Кентерис	Греция	20,08
2004	В. Кроуфорд	США	19,79
2008	У. Болт	Ямайка	19,30
2012	У. Болт	Ямайка	19,32

Хорошо видно, что и в том и другом случае рекордное время в среднем уменьшается (хотя и отнюдь не монотонно) и результаты мужчин и женщин приближаются друг к другу. В первом приближении можно попробовать аппроксимировать эти данные линейной зависимостью.

Таблица 1.4

Результаты победителей олимпийских игр в беге на 200 м,

женщины, золотые медалисты

Год	Фамилия	Страна	Время, в сек
1948	Ф. Бланкерс-Коэн	Нидерланды	24,4
1952	М. Джексон	Австрия	23,7
1956	Б. Гутберт	Австрия	23,4
1960	В. Рудольф	США	24,0
1964	Е. Макгвайр	США	23,0
1968	И. Шевинска	Польша	22,5
1972	Р. Стегер	ГДР	22,4
1976	Б. Экерт	ГДР	22,37
1980	В. Воксл	ГДР	22,03
1984	В. Бриско-Хукс	США	21,81
1988	Ф. Гриффит-Джойнер	США	21,34
1992	Г. Терренс	США	21,81
1996	М.-Дж. Перес	Франция	22,12
2000	М. Джонс	США	20,84
2004	В. Кемпбелл	Ямайка	22,05
2008	В. Кемпбелл	Ямайка	21,74
2012	Э. Феликс	США	21,88

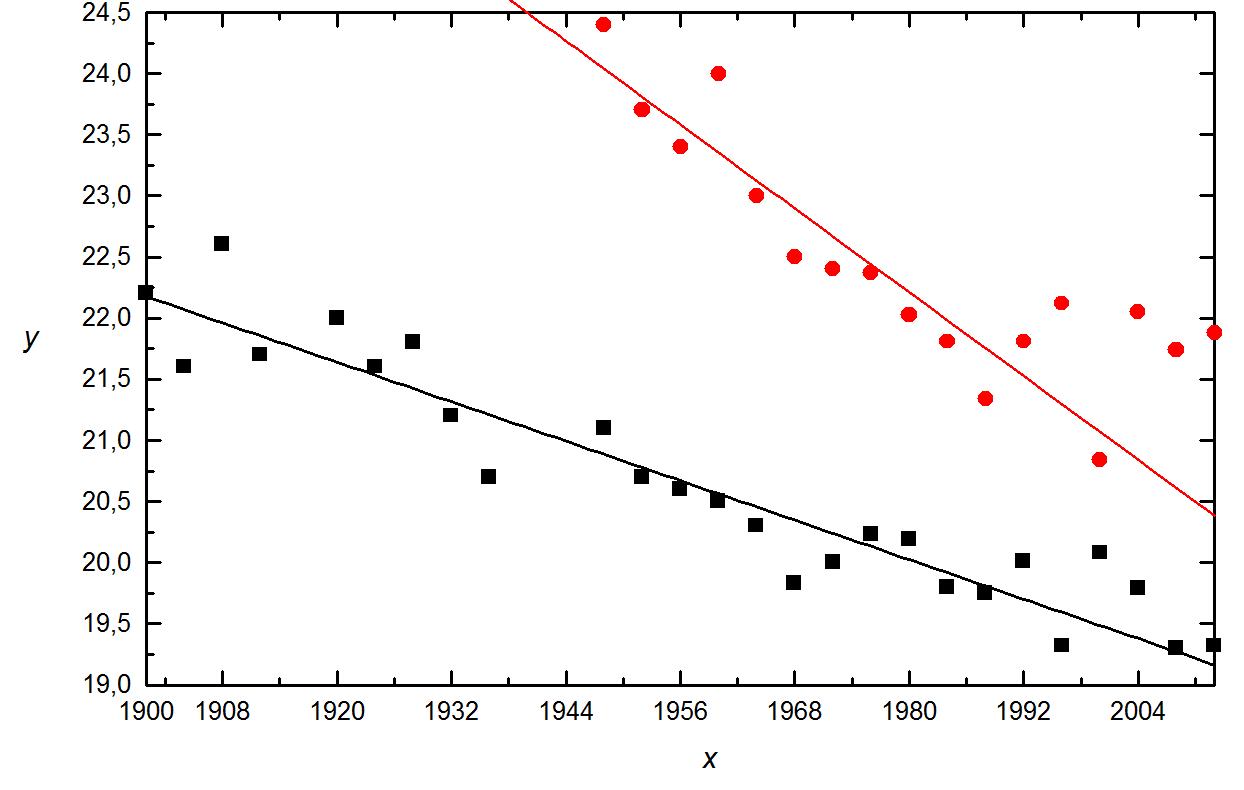
Рис. 1.3. – год, – время, в сек. Квадратиками изображены результаты мужчин, кружочками – результаты женщин. Сплошные линии (снизу и сверху) есть графики прямых (1.4) и (1.5), соответственно

Используя стандартные формулы для линейной регрессии, получим следующие результаты:

для мужчин

(1.4)

и для женщин

(1.5)

Графики полученных прямых (1.4), (1.5) показаны на рис. 1.3 сплошными линиями. Прежде чем анализировать полученный результат, отметим сразу, что точность аппроксимации в данном случае ниже, чем в первом примере. Этому соответствует меньшее значение квадрата коэффициента линейной корреляции.

Вернемся теперь к сформулированным вопросам.

Очевидно, что на первый вопрос наша модель дает заведомо неверный ответ. Действительно, например, из уравнения (1.4) следует, что в 2724 году время, за которое чемпион олимпийских игр пробежит 200 м, будет равняться нулю. Таким образом, эту модель нельзя использовать слишком далеко за пределами интервала данных, использованных при ее построении.

Ответ на второй вопрос здесь оказывается положительным: примерно в 2050 году время мужчин и женщин сравняются. Этот результат представляется более осмысленным, чем бесконечно большая скорость, однако, степень его достоверности также вызывает сомнение.

Общий вывод следующий: построенная простейшая модель не может использоваться на временах, сильно отличающихся от времен, использованных при ее построении. Следовательно, необходимо использовать более сложные функциональные зависимости.

Сформулируем основные требования к искомой функциональной зависимости: при больших временах результаты бегунов должны асимптотически стремиться к некоторому пределу сверху. Очевидно, что можно придумать бесконечное количество таких функций, однако, одной из простейших и, как правило, наиболее обоснованной зависимостью такого рода является экспоненциальная зависимость вида:

, (1.6)

где , и – неизвестные положительные числа.

К сожалению, здесь нет стандартных формул и необходимо разработать соответствующий алгоритм. Хорошо известно, что в задачах аппроксимации данных некоторой функциональной зависимостью общепринятым подходом является метод наименьших квадратов (МНК). Суть этого метода заключается в том, что неизвестные параметры искомой зависимости (в данном случае – это , и ) подбираются так, чтобы сумма квадратов отклонения функции от данных была наименьшей.

Рассмотрим использование этого общего подхода на примере функциональной зависимости (1.6). Построим базовый функционал МНК, минимум которого мы будем искать:

. (1.7)

Для определения параметров , и необходимо решить следующую систему уравнений:

(1.8)

Из (1.7) и (1.8) получим:

(1.9)

Введем обозначение , а также обозначения для математических ожиданий , и т.д. С учетом этих обозначений система (1.9) запишется в следующем виде:

(1.10)

Параметры и легко выражаются в явном виде как функции математических ожиданий , которые зависят от неизвестного параметра . Таким образом, решение системы (1.10) сводится к численному решению нелинейного трансцендентного уравнения относительно параметра . Систему (1.10) запишем в виде, более удобном для численного решения:

(1.11)

Одним из возможных методов решения системы (1.11) является метод бисекций.