1.1. Примеры эмпирических моделей

Одной из простейших задач, возникающих при математическом моделировании, является задача о нахождении эмпирической формулы с достаточной степенью точности, аппроксимирующей экспериментальные результаты.

Рассмотрим две такие задачи.

Задача 1. Продолжительность жизни птиц

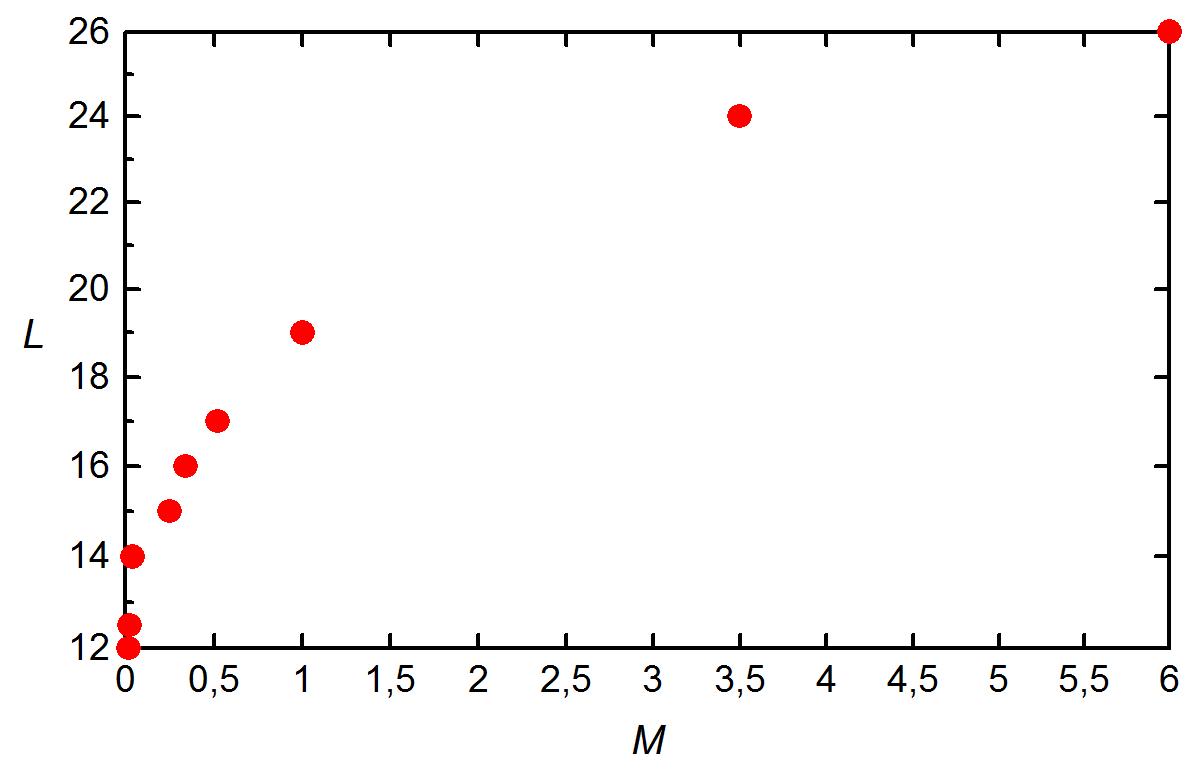
Вопрос, на который мы хотим получить ответ: какова связь между массой птицы и продолжительностью ее жизни? Исходные данные приведены в табл. 1.1.

Таблица 1.1

Птица	Масса, в кг	Продолжительность жизни, в годах
Зяблик	0,022	12
Воробей обыкновенный	0,027	12,5
Зимородок	0,045	14
Сорока	0,25	15
Ястреб-перепелятник	0,34	16
Голубь вяхирь	0,52	17
Сокол сапсан	1,0	19
Аист	3,5	24
Беркут	6,0	26

Рис. 1.1

Формулировка модели. Эта простая задача связана с нахождением приближенной формулы, отражающей наблюдаемые факты, с достаточной степенью точности. Для того чтобы лучше представить себе задачу на плоскости изобразим данные, где по оси будем откладывать массу птицы (в кг), а по оси – продолжительность ее жизни (в годах) (рис. 1.1). Из рис. 1.1 видно, что зависимость, которую мы ищем, можно представить в следующем виде:

. (1.1)

Здесь – продолжительность жизни, – масса, и – константы, обеспечивающие оптимальный результат, которые необходимо определить. Из вида приведенной зависимости от видно, что .

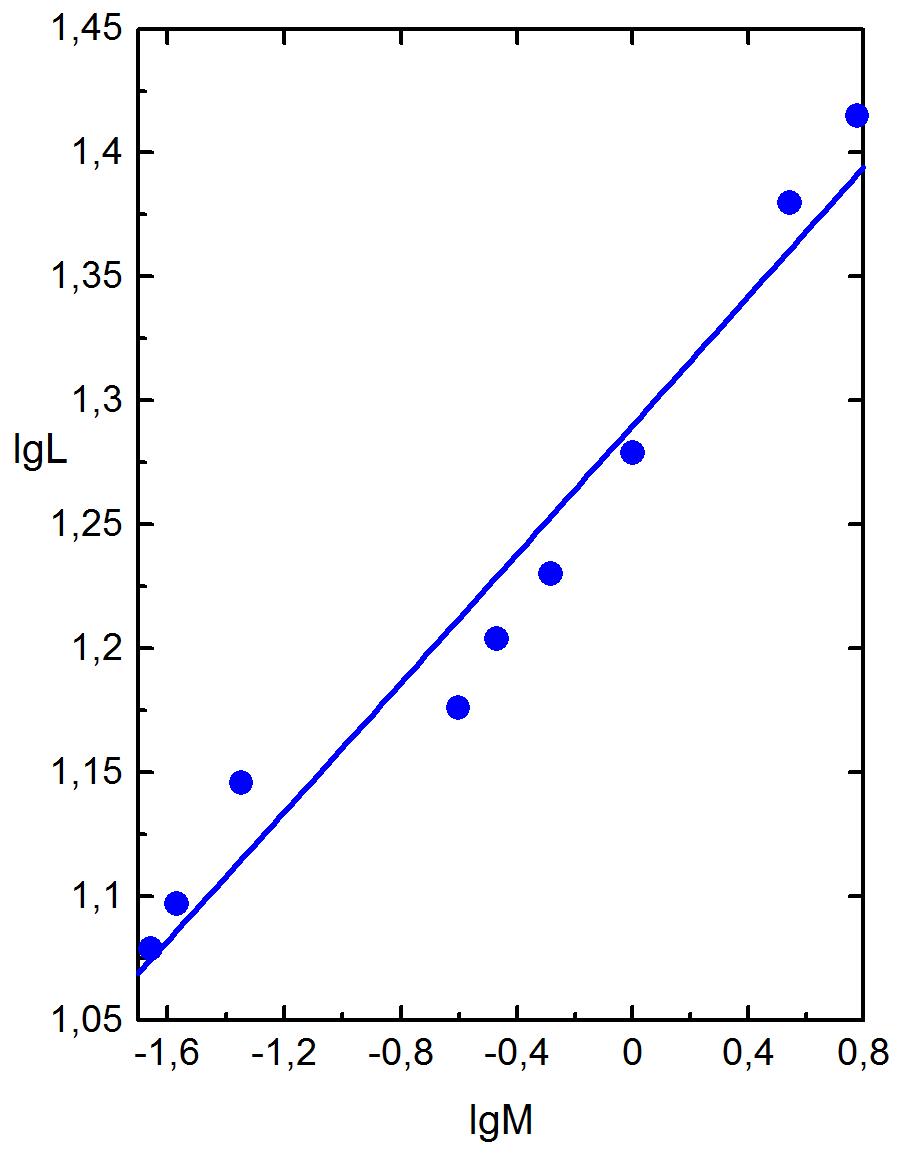
После выбора типа функциональной зависимости следующий шаг состоит в определении параметров и . Для этого предварительно прологарифмируем обе части уравнения (1.1). Это хорошо известный прием, крайне важный при анализе данных

Таблица 1.2
–1,658	1,079
–1,569	1,097
–1,347	1,146
–0,602	1,176
–0,469	1,204
–0,284	1,230
–0,000	1,279
–0,544	1,380
–0,778	1,415

(1.2)

Если функциональная зависимость (1.1) справедлива, то выражение (1.2) дает линейную зависимость от . Соответствующие данные приведены в табл. 1.2. На рис. 1.2 показана зависимость от . Из этой зависимости хорошо видно, что формула (1.1) достаточно точно передает реальную зависимость при и . Таким образом, окончательный результат имеет следующий вид:

. (1.3)

Рис. 1.2

Прямая (1.3) показана сплошной линией на рис.1.2. Формально пригодность формулы (1.3) может быть оценена при помощи вычисления коэффициента линейной корреляции . Близость этого коэффициента к единице показывает хорошую точность приближенной формулы (1.3).

Отметим важное обстоятельство, принципиальное для любой модели: окончательный результат не может быть точнее, чем точность входных данных.

В частности, очевидно, что масса птиц зависит от условий их обитания. Один тот факт, что формула (1.3) достаточно корректно описывает и зяблика, и беркута, массы которых отличаются почти в 300 раз, заставляет отнестись к этой простейшей модели с определенным доверием.

Приведенная модель является характерным представителем эмпирических моделей. Эмпирические модели – это модели, основанные на экспериментальных данных. В таких моделях связи между переменными устанавливаются, исходя из непосредственного анализа данных и выбора подходящей математической формулы, которая является компромиссом между точностью результатов и простотой математического аппарата. Всегда можно, используя более сложный математический аппарат, получить более высокую точность. Но это обычно не совсем правильный подход.

Важнейшей особенностью эмпирических моделей является то, что при их построении не делается никаких предположений, касающихся связей между переменными, и они не основываются на физических законах или иных общих принципах. Очень часто эмпирические модели используют как составные части более сложных моделей.

Рассмотрим более сложную эмпирическую модель.

Задача 2. Время победителей олимпиад в беге на 200 метров

Спортивные достижения в таких видах, как бег, интересны тем, что они постоянно меняются. Время, которое спортсмены затрачивают на преодоление определенной дистанции, уменьшается и одновременно результаты мужчин и женщин сближаются.

Сформулируем два вопроса, представляющие несомненный интерес:

а) существует ли предельное время, такое, что ни один человек не сможет пробежать данную дистанцию быстрее?

б) будет ли рекордное время женщин всегда больше, чем у мужчин?

В качестве исходных данных возьмем результаты победителей олимпийских игр в беге на 200 м с 1900 года по 2000 год у мужчин, с 1948 года по 2000 год у женщин. Эти данные приведены соответственно в табл. 1.3 и 1.4. В этих таблицах в качестве контрольных точек показаны также результаты последних трех олимпиад (2004, 2008, 2012гг).

Для того чтобы ответить на два поставленных выше вопроса, проанализируем данные. Для начала, так же, как и в предыдущей задаче, на плоскости изобразим данные, где – год, – время, в сек. (рис. 1.3).

Таблица 1.3