4.3. Третичная структура белка

Хорошо известно, что с химической точки зрения структура белка определяется последовательностью аминокислотных остатков. Однако, многие свойства белков, в первую очередь, биологические, определяются пространственной структурой, в которой каждый атом занимает строго определенное место. Эта пространственная структура и есть третичная структура белка.

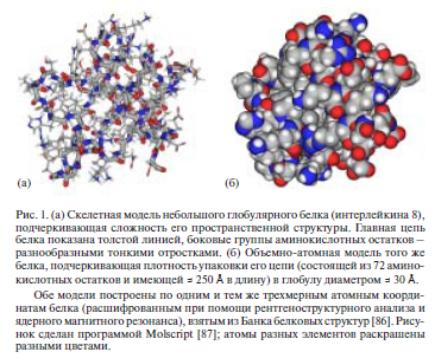
Третичная структура двух небольших белков показана на рис. 4.24, 4.25. Обе модели, показанные на рис. 4.24, построены по одним и тем же трехмерным атомным координатам белка, расшифрованным при помощи рентгеноструктурного анализа и ядерного магнитного резонанса и взятым из «Банка белковых структур».

Третичные структуры более чем 60 тысяч белков можно найти в общедоступном ресурсе «Банк белковых структур». Экспериментальное определение пространственной структуры белковых молекул – непростая задача. В то же время знание этих структур необходимо для понимания биологической функции белков. В связи с этим возникает потребность в определении третичной структуры белка путем моделирования. Прежде чем переходить к описанию математической модели, рассмотрим кратко, как происходит формирование третичной структуры в естественных условиях.

В живой клетке белок синтезируется на рибосоме. Одновременно рибосома участвует в придании белку его пространственной структуры. Помимо

Рис. 4.24. (а) Скелетная модель небольшого глобулярного белка (интерлейкина 8), подчеркивающая сложность его пространственной структуры. Главная цепь белка показана толстой линией, боковые группы аминокислотных остатков – разнообразными тонкими отростками. (б) Объемно-атомная модель того же белка, подчеркивающая плотность упаковки его цепи (состоящей из 72 аминокислотных остатков и имеющей = 250 в длину) в глобулу диаметром = 30 . Рисунок сделан программой Molscript. Атомы разных элементов раскрашены разными цветами

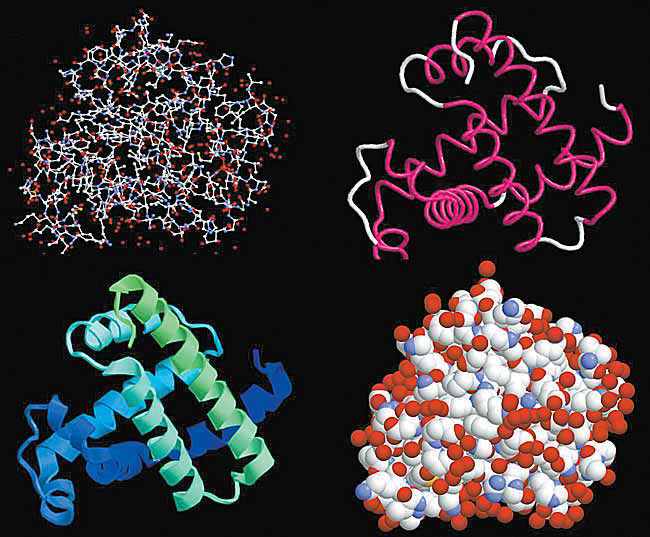
Рис. 4.25. Различные представления пространственной структуры миоглобина

рибосом в процессе сворачивания третичной структуры участвуют также специальные белки – шапероны. Однако, в начале 60-х годов ХХ века было выяснено, что сложная клеточная машинерия не является необходимым условием для формирования третичной структуры. Действительно, около 1960 года Ч. Анфинсеном с сотрудниками было сделано выдающееся открытие, за которое они получили Нобелевскую премию: глобулярный белок способен к спонтанной самоорганизации in vitro (ренатурация). Напомним, что процесс разрушения третичной структуры белка без нарушения его химической целостности называется денатурацией.

До недавнего времени вообще было непонятно, каким образом белок «выбирает» свою трехмерную структуру из громадного числа возможных. А число это действительно огромное, как в 1968 году заметил С. Левинталь. Произведем оценку числа возможных структур.

Каждый аминокислотный остаток имеет 3-4 внутренних степени свободы и, следовательно, у него существует около 10 возможных конфигураций. Поэтому даже сравнительно небольшой белок из 100 аминокислотных остатков способен находиться в конфигурациях. Известно, что время тепловой флуктуации при комнатной температуре порядка с. Отсюда следует, что для перебора всех возможных конфигураций белковой молекулы из 100 аминокислотных остатков природе потребуется около лет. Время жизни Вселенной около лет, что является пренебрежимо малой величиной по сравнению с .

Исходя из этой оценки, С. Левинталь сформулировал парадокс, впоследствии названный его именем: промежуток времени, за который белок приходит к своей третичной структуре, на много порядков меньше, чем, если бы он перебирал все возможные конфигурации.

На сегодняшний день качественное объяснение этого парадокса в основном сводится к следующему: природа выбрала именно те аминокислотные последовательности, которые быстро сворачиваются, а получившаяся структура достаточно стабильна. На самом деле, все конечно гораздо сложнее.

Вернемся теперь к моделированию.

Сформулируем задачу: зная аминокислотную последовательность белка и предполагая, что все взаимодействия между атомами молекулы известны, рассчитать третичную (пространственную) структуру белка.

Важность это задачи трудно переоценить не только с точки зрения фундаментальной науки, но и с точки зрения приложений (например, при создании новых лекарств).

Общий подход к решению поставленной задачи известен. Это методы молекулярной динамики и Монте-Карло. Они были кратко описаны выше и мы на них не будем останавливаться, тем более, что имеются общедоступные пакеты, их реализующие.

Казалось бы, вот оно решение, но есть проблема – парадокс Левинталя: если перебирать «в лоб» все конфигурации (а в принципе мы так и делаем), то на любом компьютере никогда не хватит времени (столько не живет Вселенная).

Вывод очень простой: нужны какие-то новые модели и новые методы. Какие, мы сейчас не знаем.

Завершая наше небольшое введение в математическое моделирование на примере естественных наук, оставляем читателя наедине с этой прекрасной нерешенной задачей.