4.2. Модель работы нейрона
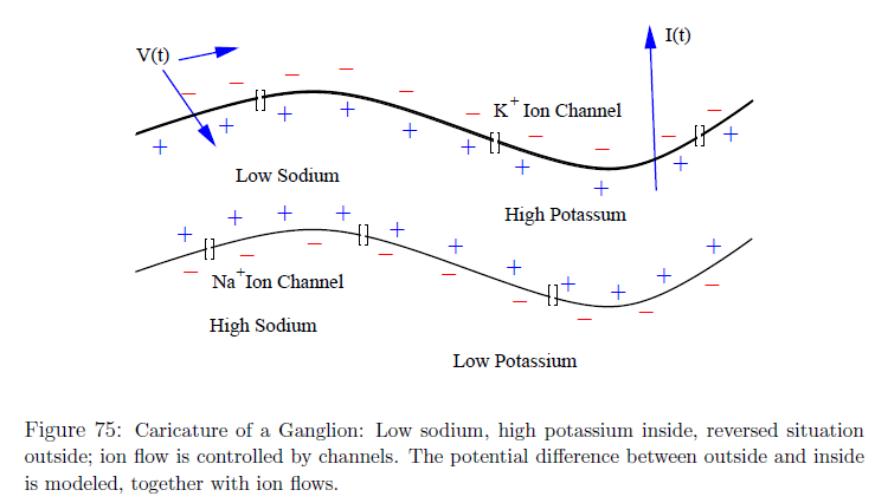
Рассмотрим классическую модель работы нейрона, известную как модель Ходжкина-Хаксли. Одной из основных функций некоторых типов клеток в организме является генерация и передача сигнала. Это могут быть, например, нейроны или клетки сердечной мышцы. В частности, за счет обмена электрическими импульсами между клетками обеспечивается синхронное сокращение сердца. Генерация и передача импульса связаны с возбудимостью клеточной мембраны.
На
языке биохимии возбудимость мембраны
описывается следующим образом. В покое
калиево-натриевый насос обеспечивает
повышенную концентрацию ионов
внутри клетки и более высокую концентрацию
ионов
снаружи. Проницаемость мембраны для
ионов
выше, чем для ионов
.
Следовательно, ионы
диффундируют в окружающую среду,
вследствие чего на мембране возникает
разность потенциалов (потенциал покоя),
равный примерно 50-70 мВ (милливольт).
Проницаемость мембран для различных
ионов есть функция потенциала. В
частности, при уменьшении мембранного
потенциала проницаемость мембран для
ионов
возрастает по сравнению с проницаемостью
для ионов
.
Этот эффект приводит в конечном счете
к распространению нервного импульса
вдоль нервного волокна. Поэтому без
поваренной соли и источников калия,
таких, как картофель, абрикосы и т.д.
жить нельзя. Длительность импульса
составляет миллисекунду, а скорость
его распространения от 1 м/с до 100 м/с.
Схематически этот механизм показан на
рис. 4.19.
|
Рис. 4.19. Схематическая модель аксона
|
Одна
из наиболее удачных моделей, описывающих
нейрофизиологические процессы, носит
название модели
Ходжкина-Хаксли
(1952 год), за которую впоследствии они
получили Нобелевскую премию. Модель
имеет четыре переменных:
– мембранный потенциал (разность
потенциалов между внутренней и наружной
сторонами мембраны);
.
Параметры
и
характеризуют проницаемость мембраны
для ионов
,
и остальных ионов, соответственно.
Более
современные модели учитывают в явном
виде большее количество типов ионов,
например, ионы
и
.
Система уравнений Ходжкина-Хаксли для одномерного случая может быть записана в виде:
(
4.35)
где
,
,
,
,
,
.
Параметры модели, принятые в оригинальной работе, следующие:
,
,
,
,
,
,
( 4.36)
Модель
Ходжкина-Хаксли, представленная в виде
системы (4.35), достаточно хорошо описывает
реальный процесс передачи нервного
импульса вдоль аксона. Исходно модель
предназначалась для описания передачи
нервного импульса в аксоне гигантского
кальмара (рис. 4.20). Поэтому все константы
и функциональные зависимости в приведенной
системе относятся именно к этому случаю
при температуре
.
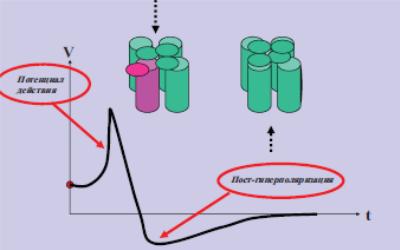
На рис. 4.21 показана расчетная зависимость
потенциала
от времени.
|
Рис. 4.20. Гигантский кальмар
|
|
Рис. 4.21. Расчетная зависимость потенциала от времени
|
Модель Ходжкина-Хаксли достаточно громоздкая и кроме ее усложнения с целью более точного описания конкретных процессов распространения нервных импульсов были предприняты попытки ее упрощения.
Наиболее успешной оказалась модель Фитцхью-Нагумо, при построении которой использовался общий подход, основанный на разделении «быстрых» и «медленных» переменных.
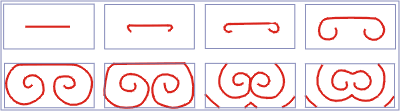
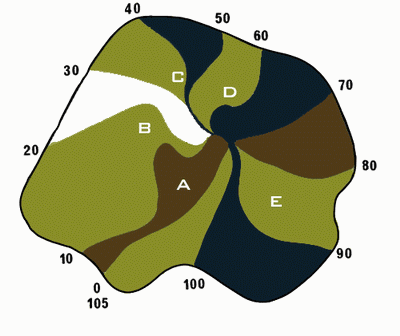
На рис. 4.22 показаны спиральные волны возбуждения, полученные в результате моделирования в рамках этой модели, а на рис. 4.23 показаны спиральные волны возбуждения, обнаруженные экспериментально в сердце кролика.
|
Рис. 4.22. Спиральные волны возбуждения, полученные в результате моделирования, в рамках модели Фитцхью-Нагумо
|
|
Рис. 4.23. Спиральные волны возбуждения, обнаруженные экспериментально в сердце кролика
|
Уравнения модели Фитцхью-Нагумо имеют следующий вид:
(
4.37)
где
– «быстрая» переменная, соответствующая
мембранному потенциалу в полной модели;
– «медленная»
переменная;
– параметры модели, причем
.
Обратите внимание, что в сердце не только
кролика, но и в нашем, могут существовать
спиральные волны возбуждения.
Кроме модели Фитцхью-Нагумо, были предложены и другие упрощенные модели передачи нервного импульса, такие, как модель Алиева-Панфилова, модель Зимана и др.
Завершая краткий обзор математических моделей в биологии, рассмотрим вопрос о моделировании третичной структуры белка.