Глава 1. Основные понятия и примеры математических моделей
Чем отличается приложение математики от чистой математики? Важно помнить, что приложение математики и чистая математика – это очень разные виды деятельности. Умения, необходимые для того чтобы быть успешным в приложениях математики, совершенно отличаются от тех, которые необходимы для понимания общих математических концепций, доказательств теорем или решений уравнений.
В предлагаемом пособии теория сведена к минимуму и излагаются лишь очень немногие общие подходы. Однако, не следует думать, что математическое моделирование – легкий предмет. Трудность математического моделирования состоит не в изучении необходимой математики (хотя зачастую используемая математика достаточно сложная), а в умении увидеть, где и как эта математика может быть использована.
Математическим базисом моделирования являются вычислительные методы различной природы. Существует много примеров очень простой математики, дающей решение очень сложных проблем, хотя в целом сложность проблемы и сложность необходимой математики идут рука об руку. Специалисты, профессионально занимающиеся математическим моделированием, имеют дело с самыми различными реальными проблемами, и их основной задачей является перевод каждой проблемы в математическую форму. Это есть суть математического моделирования.
Попробуем теперь объяснить основную идею математического моделирования и почему оно так важно. Вряд ли точные определения очень существенны на этой стадии изучения математического моделирования. Скорее проще и полезнее привести характерные примеры, из анализа которых мы сможем понять суть математического моделирования. Любая модель (включая физические модели) может быть определена как упрощенное представление определенных аспектов реальной системы.
Математическая модель – это модель, созданная с использованием математических концепций, таких, как функции, уравнения и другие. Так же, как и при создании любой модели, создание математической модели подразумевает переход от реального мира к миру абстрактных математических концепций, в терминах и понятиях которых и строится модель. Далее мы «решаем» модель, т.е. проводим ее исследование в «сухом» мире математических абстракций. И, наконец, мы снова возвращаемся в реальный мир, принося с собой решение математической задачи, которое переводится в некоторое полезное утверждение, относящееся к реальной проблеме реального мира.
Отметим еще раз самое важное свойство любого моделирования, в том числе и математического: отправной и конечной точкой всегда является реальный мир.
Не следует думать, что для конкретной проблемы из реального мира существует единственная «правильная» модель. Здесь принципиальное отличие от чистой математики, будь то арифметика или топология, где на каждый вопрос существует один единственный правильный ответ (мы не будем конечно углубляться в тонкости основания математики, где все не так просто). Для одной и той же системы могут быть построены различные модели, описывающие ее на разных языках и с разной степенью точности. Заметим, что математика обладает удивительным свойством одними и теми же моделями описывать совершенно различные реальные системы. Знаменитый физик Юджин Вигнер (Eugene Wigner), завороженный блеском математики, одну из своих статей озаглавил «Непостижимая эффективность математики в естественных науках».
В
некотором смысле одни модели могут быть
«лучше» других. Обычно это означает
либо простоту и удобство применимости,
либо более высокую точность предсказаний.
Чаще всего успех модели зависит от того,
насколько она точна и легка в использовании.
Заметим, что понятие «легкости»
существенно зависит от развития
вычислительной техники. Любые модели
имеют ограниченную
область применимости
и не могут использоваться за пределами
этой области. Классическим примером
может служить механика Ньютона, которая
применима только при скоростях
много меньших, чем скорость света (
).
Еще одной специфической особенностью математического моделирования является коллективность. Как правило, в отличие от чистой математики, создание и исследование математической модели – плод коллективного творчества. Наиболее четко это проявляется в промышленности, где практически всегда работает команда, состоящая из инженеров, экономистов, математиков, программистов и т.д. Коллективный дух моделирования необходимо воспитывать с самого начала. Хотя данное пособие будет читаться индивидуально, хочется надеяться, что те упражнения по математическому моделированию, которые вы будете получать на практических занятиях, вы будете решать в командах. Вспомните: сколько людей, столько и моделей!
Чтобы добиться успехов в математическом моделировании, недостаточно владеть математической техникой, статистикой или программированием. Главное – это ясный ум, логическое мышление, интуитивное ощущение порядка величин, способность к общению и, конечно, стремление решить задачу.
Завершая общее описание математического моделирования, сформулируем основные выводы:
Построение математической модели всегда начинается с построения модели на языке предметной области.
Математическое моделирование заключается в приложении ваших математических знаний для получения ответа на задачи, поставленные реальностью.
Математические модели могут использоваться для очень широкого спектра задач, многие из которых представляются в первый момент совсем не математическими по своей природе.
В математическом моделировании нет жёстких правил, законов и не существует единственных правильных ответов.
Научиться моделированию можно только путём моделирования.
Математическое моделирование – это коллективный творческий процесс специалистов предметной области и математиков.
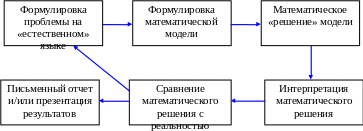
Окончательно работу специалиста, занимающегося математическим моделированием, можно представить в виде следующей схемы:
|
Опишем теперь содержание каждого этапа.
Этап 1. Формулировка проблемы на «естественном» языке
Что в действительности мы хотим знать? Каковы наши цели? Как мы сможем оценить результат? Каковы источники фактов и данных и насколько они достоверны? Существует ли единственный ответ на поставленный вопрос? Проблема должна быть классифицирована – детерминисткая или стохастическая? И, наконец, нужно ли вообще моделировать?
Этап 2. Формулировка математической модели
Рассмотрите вначале простейшую модель. Нарисуйте графическое представление функциональных зависимостей. Составьте список важных факторов. Соберите необходимые данные и определите их значимость. Если необходимо, расширьте спектр входных данных. Для каждой переменной введите удобное обозначение. Зафиксируйте те допущения, которые вы хотите использовать. Запишите уравнения, связывающие введенные переменные, используя ваши знания математики.
Этап 3. Математическое «решение» модели
Используйте алгебраические и/или численные методы, дифференциальное исчисление, теорию графов и т.д. Напишите программу на одном из языков высокого уровня (С++, Фортран и т.д.) или используйте уже готовый пакет. Представьте полученные результаты в графической или табличной форме.
Этап 4. Интерпретация математического решения
Изучите результаты, полученные в ходе систематического решения проблемы. Имеют ли полученные значения переменных нужный знак и величину? Соответствуют ли вычисленные интервалы возрастания и убывания наблюдениям? Рассмотрите предельные значения вычисленных величин. Получили ли вы достаточно «хорошее» решение или необходимо какие-то изменения в исходных данных или в самой модели?
Этап 5. Сравнение математического решения с реальностью
Могут ли ваши результаты быть проверены сравнением с реальными данными? Имеет ли смысл полученное решение? Согласуются ли ваши предсказания с реальными данными? Соответствуют ли полученные результаты тем задачам, которые ставились? Требуется ли более высокая точность как в построении самой модели, так и в вычислительных алгоритмах? Может ли быть построена более совершенная модель?
Этап 6. Письменный отчет и/или презентация результатов
Для кого пишется отчет и что читатель хочет знать? Насколько подробным должен быть отчет?
Приведенная выше методология может показаться излишне сложной, однако, нет необходимости придерживаться изложенного алгоритма слишком жестко. Сама суть математического моделирования подразумевает гибкость.