Модель Вольтерра и ее обобщения

Перейдем к описанию конкретных моделей. Начнем с классической модели Вольтерра и ее обобщений. В основу своих работ Вольтерра положил следующие простые гипотезы:

1. Пища либо имеется в неограниченном количестве, либо ее поступление с течением времени лимитировано.

2. Существует естественная смертность особей каждого вида.

3. Хищники поедают жертв, причем количество съеденных жертв пропорционально вероятности встречи хищника и жертвы, т.е. произведению количества хищников на количество жертв.

4. Если имеется несколько видов потребляемой пищи, имеющейся в ограниченном количестве, то доля потребляемой в единицу времени пищи пропорционально количеству особей.

5. Если вид питается пищей, количество которой неограниченно, то его прирост пропорционален численности.

6. Если пища имеется в ограниченном количестве, то прирост численности вида пропорционален количеству съеденной пищи.

Гипотезы 1)-6) в сущности аналогичны представлениям классической химической кинетики и закону действующих масс.

Для двух видов, численность которых обозначается как и , в соответствии с гипотезами Вольтерра 1)-6) можно записать следующую систему уравнений:

( 4.24)

Если положить , т.е. взаимодействие между видами отсутствует, то мы получаем два логистических уравнения, решения которых хорошо известны. Если хотя бы один их коэффициентов и отличен от нуля, то виды начинают взаимодействовать.

Рассматривая различные комбинации значений коэффициентов , , выделим три важнейших класса:

1. – симбиоз;

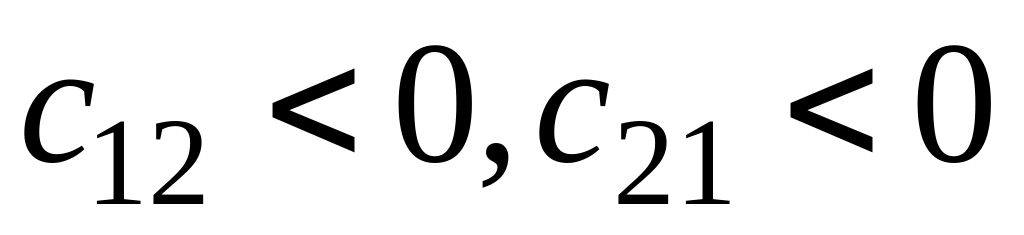2. – конкуренция;

3. – хищник–жертва.

Наибольший интерес представляют для нас два последних случая: конкуренция и хищник–жертва.

Рассмотрим стационарные состояния системы (4.24), которые определяются из следующих уравнений:

( 4.25)

Система (4.25) имеет четыре решения:

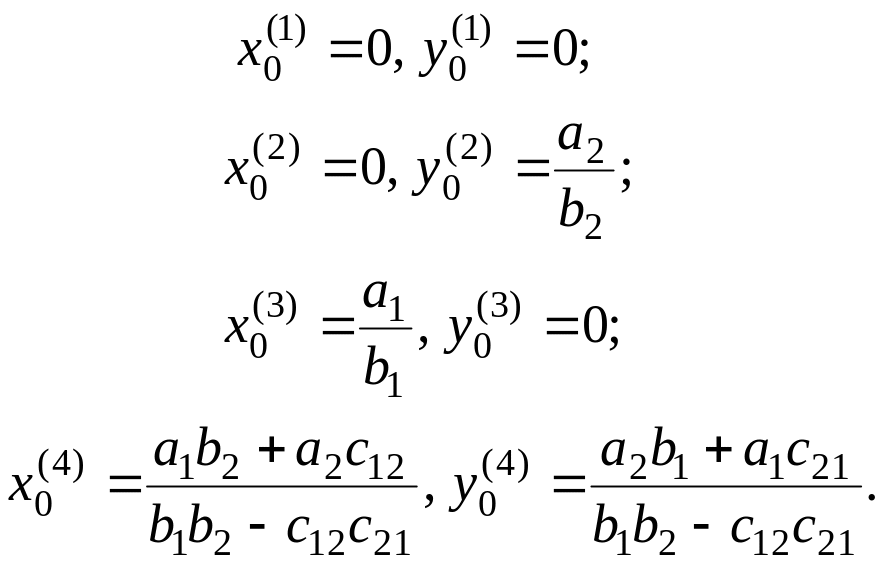( 4.26)

Перейдем теперь к модели конкуренции ( ) и исследуем стационарные состояния:

1. Стационарное состояние (0,0) всегда неустойчивый узел.

2. Стационарное состояние является седлом при 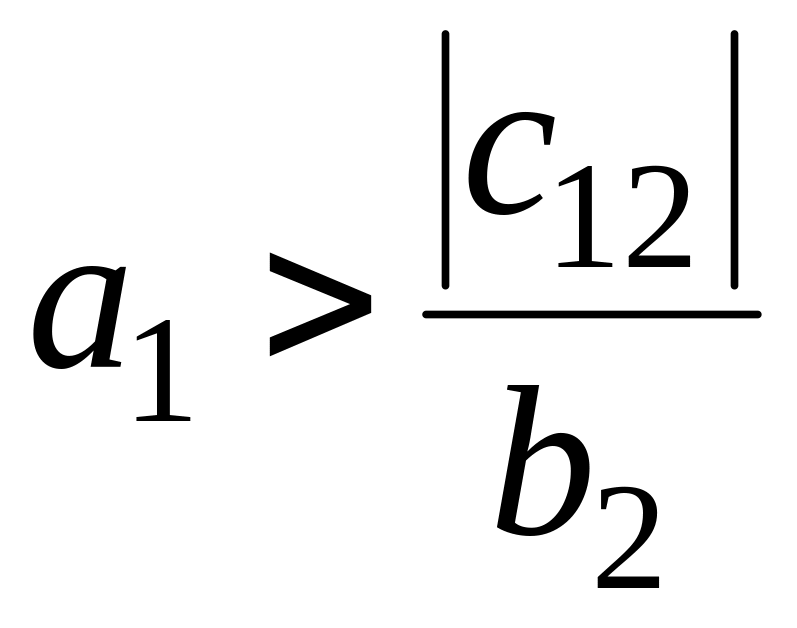и устойчивым узлом в противном случае. Это означает, что вид вымирает, если его собственная скорость роста меньше некоторой критической величины.

3. Стационарное состояние аналогично (2).

4. Это стационарное состояние характеризует сосуществование двух конкурирующих видов и в ряде случаев представляет собой устойчивый узел.

Сделав линейную замену переменных в системе (4.24), можно привести ее к виду, содержащего всего три параметра:

( 4.27)

где стационарные точки определяются как

. ( 4.28)

Проанализируем возможные типы фазовых портретов. Для этого рассмотрим так называемые главные изоклины системы. Напомним определения:

1) Изоклиной на фазовой плоскости называется кривая, такая, что в каждой ее точке вектор скорости принимает некоторое постоянное значение.

2) Главными изоклинами называются изоклины, для которых либо , либо .

Очевидно, что пересечение главных изоклин дает стационарные точки системы.

В данном случае имеется всего 4 главных изоклин, представляющих собой прямые линии.

Изоклины, на которых – ; изоклины, на которых – .

Заметим, что сами оси и являются изоклинами.

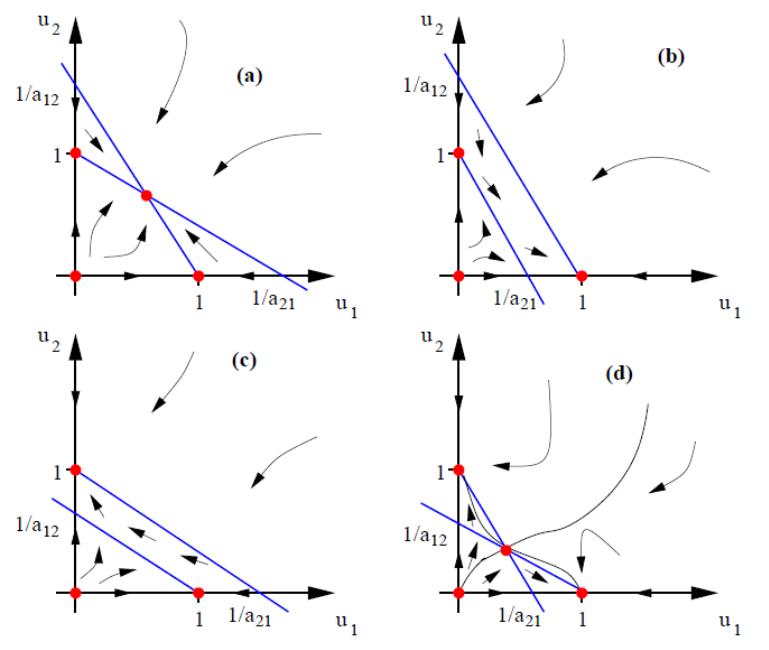
В первой четверти декартовой плоскости мы имеем четыре различных типа фазовых портретов, показанных на рис. 4.12.

(а) . Здесь внутри положительного квадранта существует точка пересечения изоклин, которой соответствует точка сосуществования двух видов. Векторное поле скоростей показывает, что это стационарное состояние устойчиво (устойчивый узел).

Рис. 4.12. Качественно различные типы фазовых портретов в первом квадранте. Стационарные точки показаны красными кружочками, а изоклины (кроме осей координат) – голубыми линиями

(b) . Здесь стационарные состояния расположены на границах положительного квадранта, т.е. сосуществование видов невозможно.

(c) . Случай полностью аналогичен случаю (b).

(d) . Как и в случае (а), существует стационарное состояние, соответствующее сосуществованию видов, однако, в данном случае оно неустойчивое (седло) и устойчивыми являются граничные стационарные состояния (0,1) и (1,0). Это означает, что в системе существует множественность стационарных состояний, т.е. в зависимости от начальных условий система стремится либо к стационарному состоянию (1,0), либо к стационарному состоянию (0,1).

Основной результат, полученный нами, сводится с математической точки зрения к следующему утверждению: Устойчивое стационарное состояние внутри первого квадранта существует в случае , т.е. когда взаимодействие между двумя видами достаточно слабо.

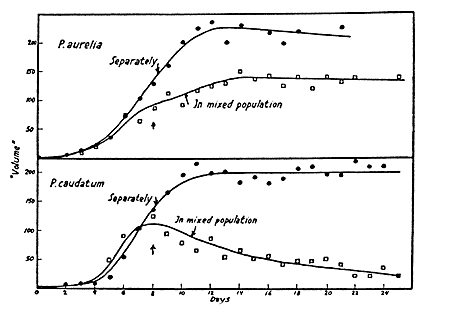
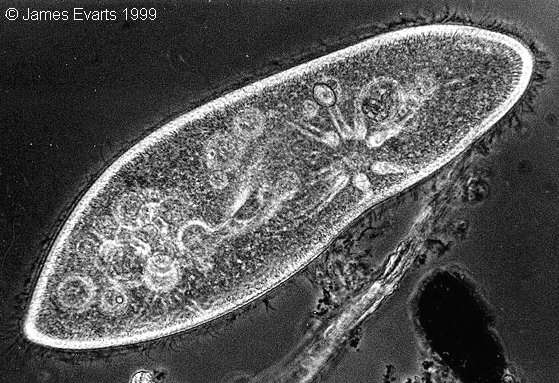
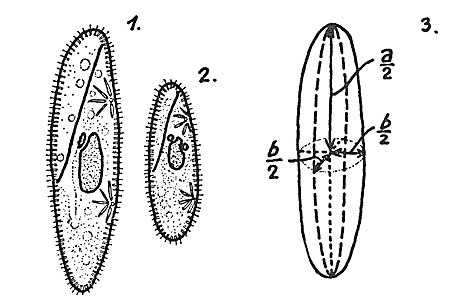
На языке биологии мы получаем следующее фундаментальное утверждение: Закон конкурентного исключения (Г. Гаузе) – в одной экологической нише может существовать только один вид. На рис. 4.13 приведены результаты эксперимента Гаузе для двух видов инфузорий-туфелек Paramecium. Туфельки –это крупные одноклеточные ­­­­­эукариоты, длина которых в зависимости от вида (их несколько сотен) колеблется от 50 до 350 микрон. Paramecium Aurelia и Paramecium Caudatum, использованные в экспериментах Гаузе, показаны на рис. 4.14. На рис. 4.15 показаны относительные размеры этих двух видов.

Рассмотрим теперь случай разных знаков коэффициентов , . Это одна из простейших моделей «хищник-жертва» или модель Лотки-Вольтерра с логистической поправкой. Ее можно исследовать тем же самым способом, что и проанализированная подробно модель конкуренции двух видов. Мы не будем этого делать, а приведем лишь самый главный результат. В этой модели ни при каких значениях параметров невозможны устойчивые (незатухающие) колебания численности обоих видов. Стационарное состояние, соответствующее сосуществованию хищника и жертвы, может быть либо устойчивым, либо неустойчивым фокусом. Это означает, что мы будем наблюдать либо затухающие колебания, либо, наоборот, растущие.

Рис. 4.13. Результаты эксперимента Гаузе для двух видов инфузорий-туфелек Paramecium: сверху рисунка P. aurelia, снизу – P. caudatum. По горизонтальной оси отложены дни, по вертикальной оси – объем популяций туфелек. Заполненные (незаполненные) кружки показывают экспериментальные данные для популяций без конкуренции (с конкуренцией).

а)	б)
Рис. 4.14. Paramecium Aurelia (а) и Paramecium Caudatum (б), использованные в экспериментах Гаузе

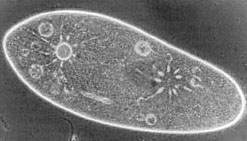
Рис. 4.15. Относительные размеры двух видов: 1. P. caudatum; 2. P. aurelia

В то же время хорошо известно, что в реальных популяционных системах наблюдаются незатухающие колебания численности видов (рис. 4.16). Более того, обычно утверждается, что именно модель Лотки-Вольтерра описывает такие колебания.

Рассмотрим этот вопрос подробнее. Проанализируем оригинальную модель Лотки-Вольтерра, которая является упрощенным вариантом модели, описанной выше. Отличие заключается в том, что вместо логистического вида правых частей уравнения в отсутствии межвидового взаимодействия (то, что использовалось нами) в исходных уравнениях

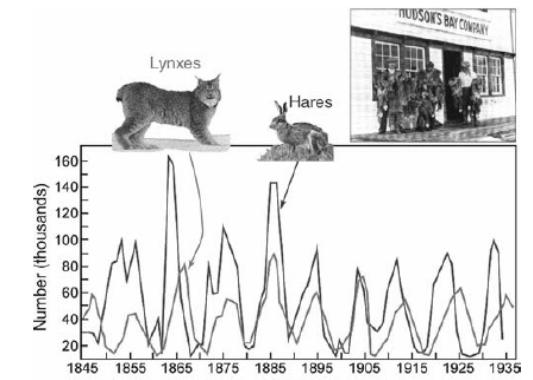
Рис. 4.16. Количество шкурок рысей и зайцев, сданных на приемные пункты компании «Hudson’s Bay Company» (Канада). По горизонтальной оси отложены годы, по вертикальной оси – количество шкурок в тысячах штук

Лотки-Вольтерра правые части имели «мальтузианский» вид – неограниченное экспоненциальное размножение жертв и такая же экспоненциальная смерть хищников. Запишем эти уравнения, сохранив наши обозначения, в следующем виде:

( 4.29)

Здесь и . Для простоты обозначения положив , , из (4.29) получим

( 4.30)

Проведем, так же, как и ранее, исследование стационарных состояний. Теперь их только два: (0,0) и . Покажем, что второе стационарное состояние, соответствующее сосуществованию популяций, является центром. Действительно, линеаризованная система в этой точке принимает следующий вид:

( 4.31)

Запишем характеристическое уравнение:

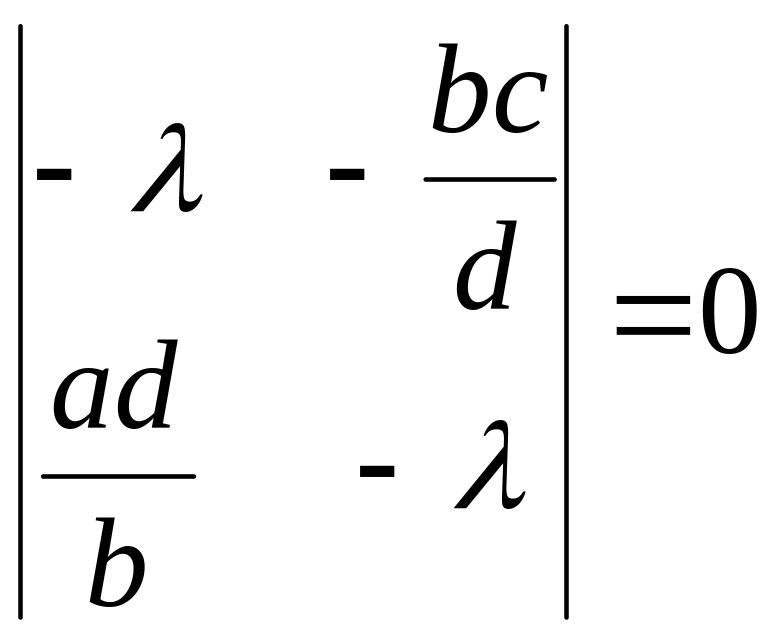. ( 4.32)

Корни уравнения (4.32) . Следовательно, стационарное состояние является центром. Кинетические кривые системы (4.30) показаны на рис. 4.17.

Рис. 4.17. Кинетические кривые системы (4.30). По горизонтальной оси отложено время (в усл.ед.), по вертикальной оси – объем популяций (в усл.ед.)

Видно, что численность обеих популяций меняется периодически, т.е. имеют место незатухающие колебания. Казалось бы, все хорошо и мы имеем модель, достаточно адекватно отображающую реальную действительность. Однако, к сожалению, стационарная точка, вокруг которой происходят колебания, является центром. А это – негрубая стационарная точка, т.е. она неустойчива относительно сколь угодно малых изменений правой части уравнения. Именно этот эффект мы видели в более сложной модели с логистическими добавками, в которой центр превращается в устойчивый или неустойчивый фокус. Таким образом, на самом деле исходная модель Лотки-Вольтерра не описывает незатухающие колебания, имеющие место в реальных системах. По существу мы приходим к выводу, что для описания незатухающих колебаний численности популяций необходимо построение моделей более сложных, чем рассмотренные выше.

Рассмотрим соответствующий пример. Это так называемая модель Розенцвейга-Макартура. В общем виде она записывается как

( 4.33)

где – скорость изменения численности жертв в отсутствии хищников, – скорость уменьшения количества жертв из-за наличия хищников, – коэффициент смертности хищников (в «мальтузианском» виде), – коэффициент эффективности усвоения жертв хищниками.

Вид функций и естественно меняется от модели к модели в зависимости от конкретной биологической системы.

Приведем одну из таких моделей, предложенной Макартуром, которая описывает взаимодействие двух видов насекомых:

( 4.34)

В первом уравнении описываются следующие процессы: насекомые вида поедают личинок вида (член ), но взрослые особи вида поедают личинок вида при условии высокой численности видов или , или обоих видов (члены ).

Во втором уравнении член отражает скорость прироста вида ; – логистическая добавка; – поедание личинок вида насекомыми вида ; – увеличение популяции вида за счет поедания личинок вида .

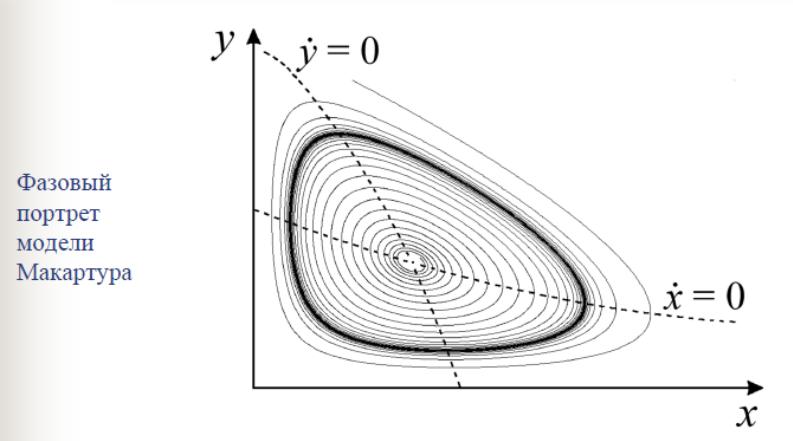
Рис. 4.18. Фазовый портрет модели Макартура

Характерный фазовый портрет для системы (4.34) показан на рис. 4.18. Пунктирными линиями показаны главные изоклины. Хорошо виден предельный цикл, соответствующий незатухающим колебаниям численности популяций обоих видов.

Популяционная динамика, начиная с работ Вольтерры – традиционный объект математической биологии. Простейшим объектом моделирования являются микробные сообщества, наподобие рассмотренным нами сообществ туфелек. А сложнейшим и уникальным объектом является вся биосфера Земли. На этом мы закончим обзор моделей популяционной биологии, отсылая читателя к соответствующим монографиям, учебниками и учебным пособиям.

Перейдем теперь к построению моделей иного типа.