Модели взаимодействующих видов

Логистическое уравнение, рассмотренное выше, описывает конкуренцию в пределах одного вида. Как только мы начинаем рассматривать два взаимодействующих вида, то вместо одного дифференциального уравнения получаем систему из двух дифференциальных уравнений. Прежде чем начать изучение конкретных моделей взаимодействующих видов, рассмотрим основные понятия теории систем обыкновенных дифференциальных уравнений, делая упор на их качественное исследование.

Система двух автономных дифференциальных уравнений в общем виде записывается как

( 4.16)

где – непрерывные функции. Будем также полагать, что эти функции дифференцируемы по и . Стационарные состояния системы (4.16) определяются из системы алгебраических уравнений:

( 4.17)

Решение системы (4.16) может быть представлена как кривая в трехмерном пространстве . Спроектировав эту кривую на плоскость , получим траекторию системы на фазовой плоскости. Совокупность фазовых траекторий, отвечающих различным начальным значениям , называется фазовым портретом системы. Отметим, что стационарной точке в пространстве соответствует прямая, перпендикулярная плоскости и пересекающая ее в точке .

Вначале рассмотрим возможное поведение линейной однородной системы двух дифференциальных уравнений:

( 4.18)

где – действительные числа.

Пусть . Если , то система (4.18) имеет единственное стационарное состояние (0,0). Если , то стационарные точки системы либо лежат на некоторой прямой, проходящей через начало координат, либо заполняют всю плоскость .

Случай неоднородной линейной системы сводится к рассматриваемому случаю однородной системы путем сдвига начала координат. Поведения решений системы (4.18) определяется собственными значениями матрицы . В данном случае выражение для собственных значений легко записывается в явном виде:

. ( 4.19)

Введем обозначения: . Тогда выражение (4.19) запишется в более удобном для дальнейшего анализа виде:

. (4.20)

Рассмотрим возможные варианты различного поведения системы, их можно разбить на вырожденные и невырожденные (табл. 4.1). Отметим, что невырожденный случай устойчив относительно малых шевелений параметров .

Таблица 4.1

Невырожденный случай	Вырожденный случай
, ,	1. , ,
, ,	2. , ,
,	3. ,
,	4. ,
,	5. ,
	6.

Заметим, что в реальных биологических системах вырожденный случай в действительности не встречается.

Общее решение системы (4.18) для невырожденного случая может быть записано как

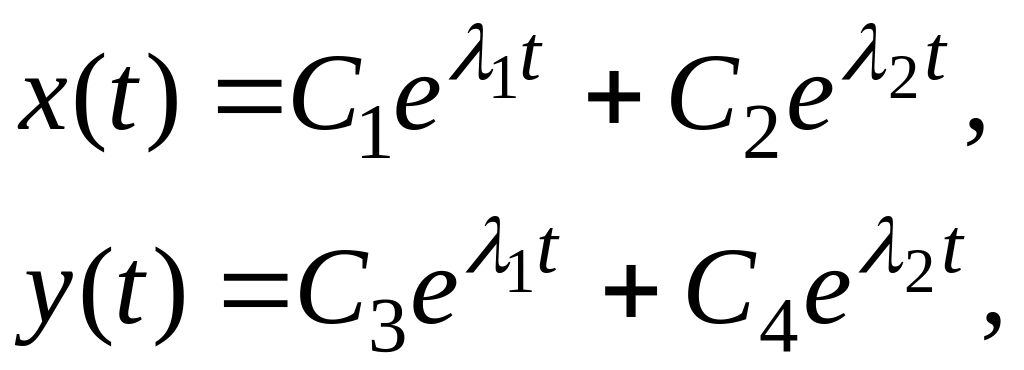( 4.21)

где – произвольные числа.

Проанализируем стационарное состояние (0,0) в соответствии с приведенной классификацией системы (4.18).

Начнем с невырожденного случая.

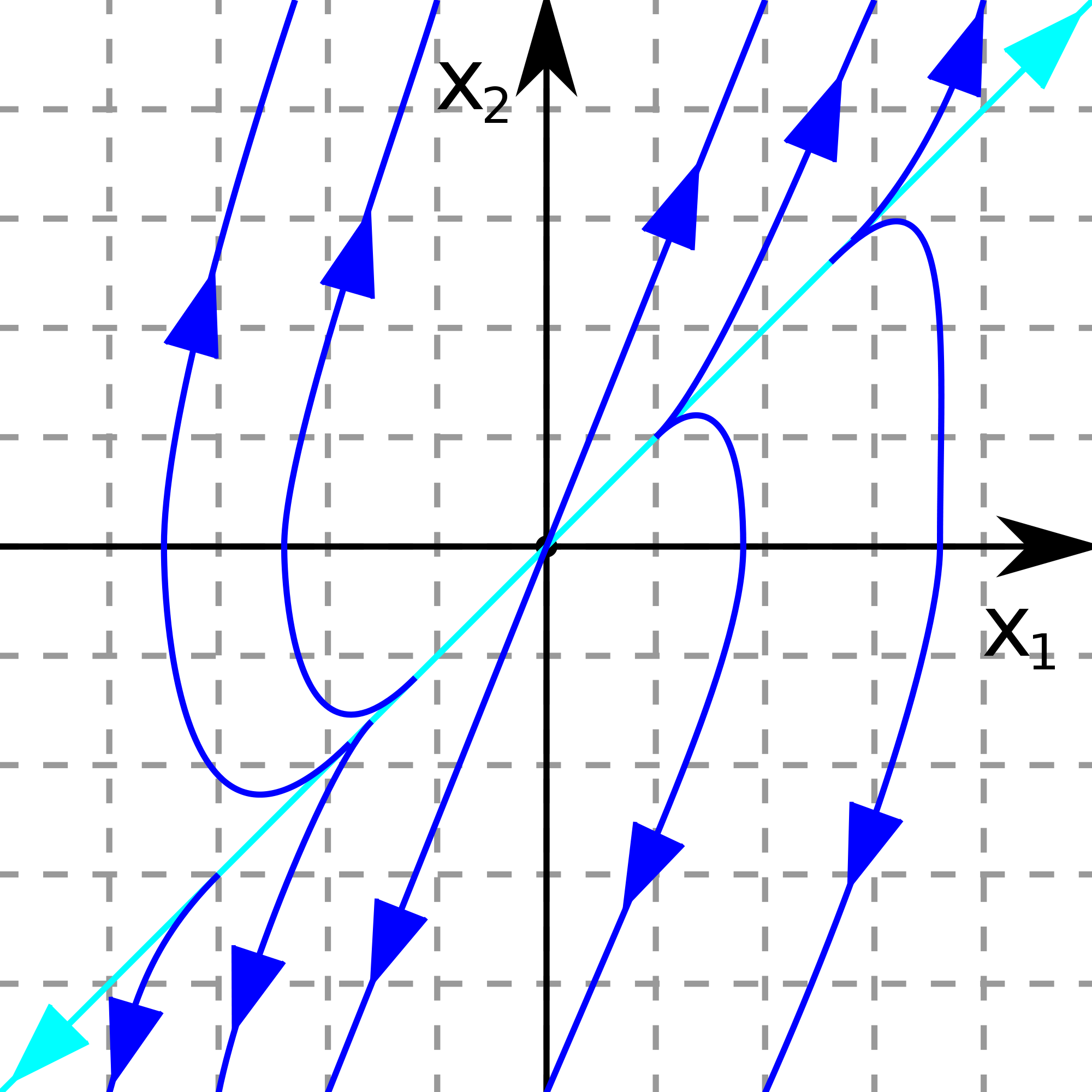
1. , , . Очевидно, что с увеличением траектории (4.21) системы на плоскости уходят на бесконечность. Таким образом, стационарное состояние неустойчиво и называется неустойчивым узлом. Соответствующий фазовый портрет показан на рис. 4.5.

2. , , . В этом случае стационарное состояние не только устойчиво, но и асимптотически устойчиво по Ляпунову, и называется устойчивым узлом (рис. 4.6).

Рис. 4.5. Неустойчивый узел	Рис. 4.6. Устойчивый узел

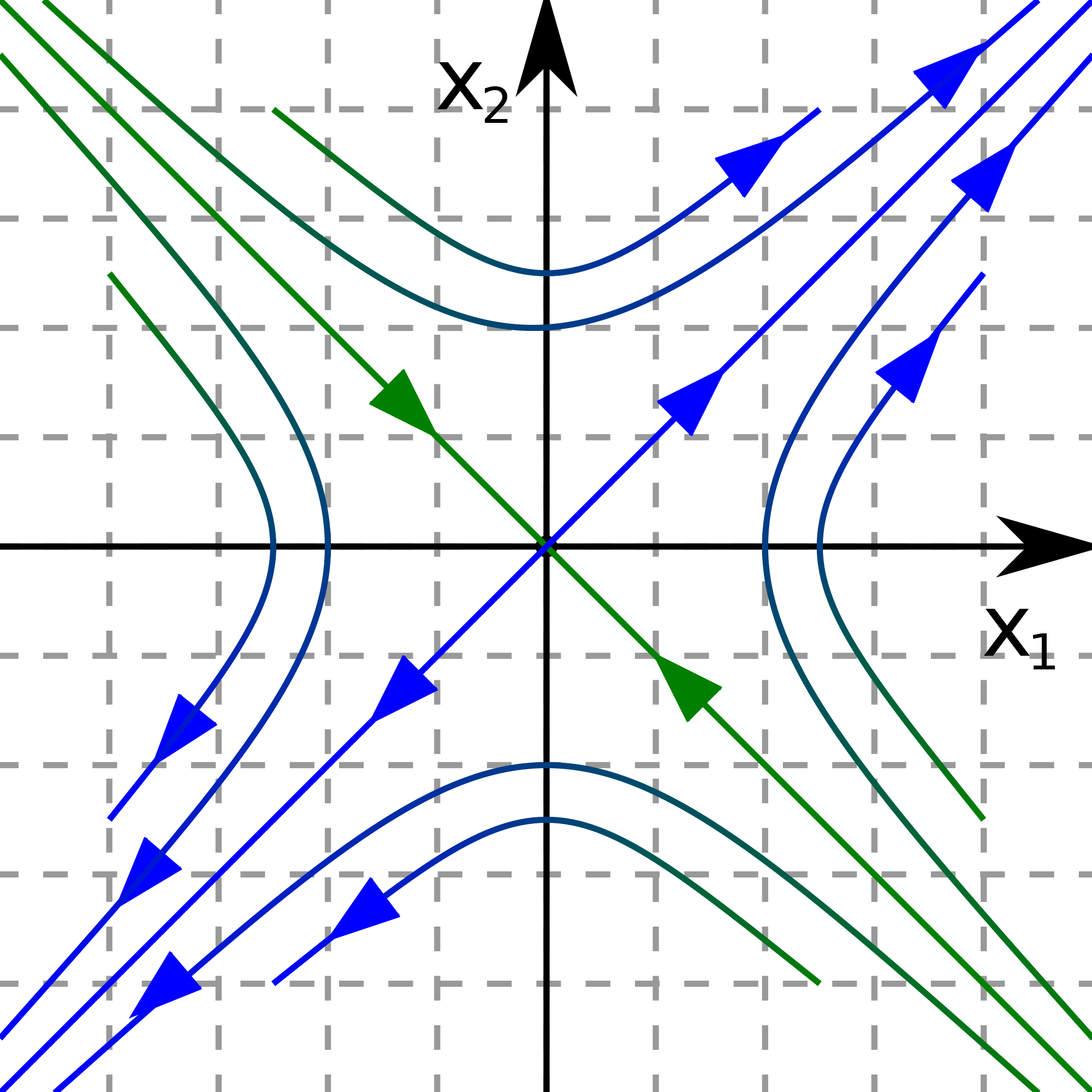
Рис. 4.7. Седло

3. , . Стационарное состояние неустойчиво и называется седлом (рис. 4.7). Заметим, что существует единственная траектория, двигаясь по которой, точка будет неограниченно приближаться к стационарному состоянию.

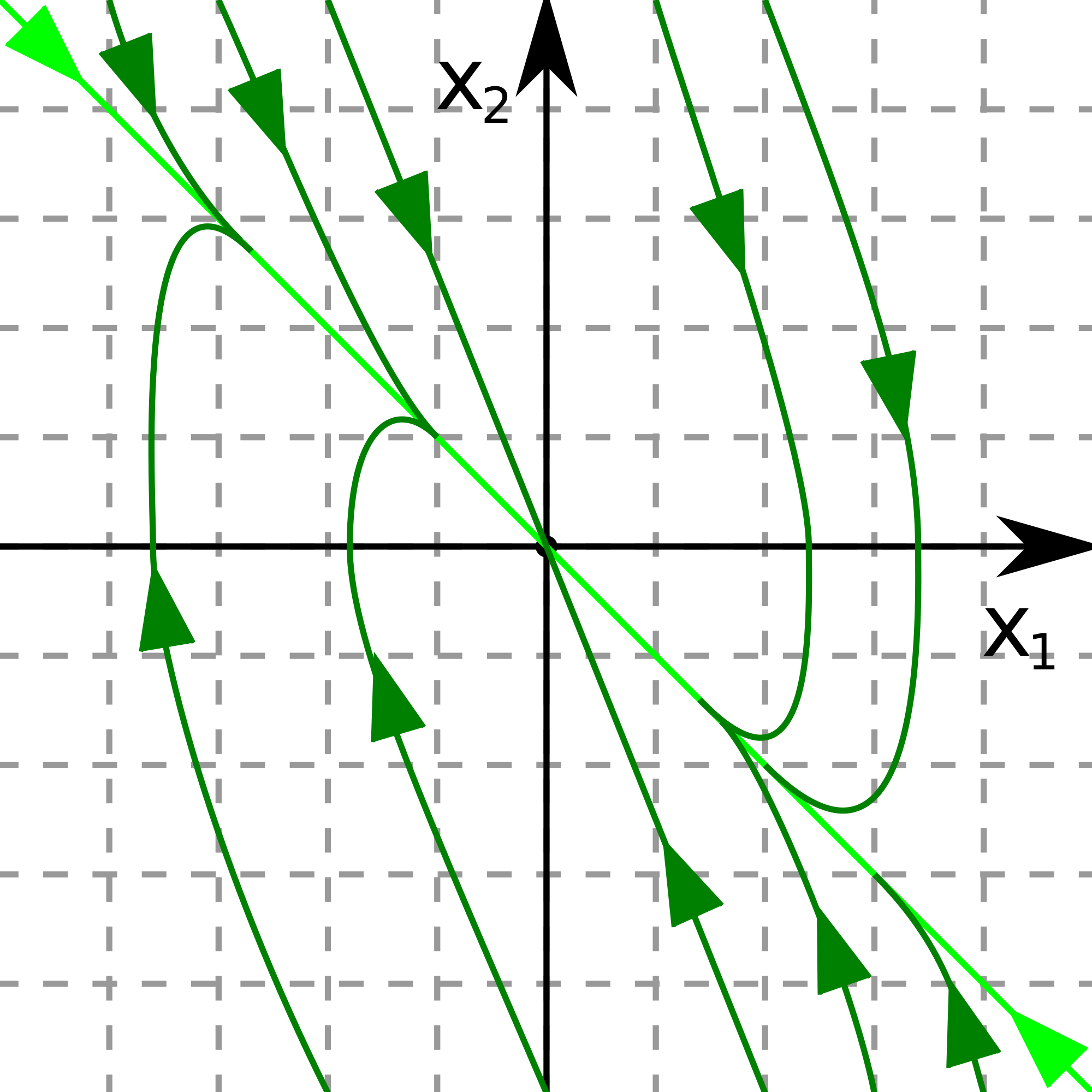
4. , . Стационарное состояние неустойчиво и называется неустойчивым фокусом (рис. 4.8) – возрастающие колебания.

5. , . Стационарное состояние устойчиво и называется устойчивым фокусом (рис. 4.9) – затухающие колебания.

Легко видеть, что тип стационарного состояния для всех пяти рассмотренных случаев не меняется при малом шевелении параметров . Такие стационарные состояния называются грубыми. Их важность очевидна: во всех реальных биологических системах возможны только грубые стационарные состояния.

Из вырожденных стационарных состояний рассмотрим только .

Рис. 4.8. Неустойчивый фокус	Рис. 4.9. Устойчивый фокус

Рис. 4.10. Центр

Это стационарное состояние называется центром и его фазовый портрет показан на рис. 4.10. Решение имеет вид незатухающих колебаний. Аналогичные незатухающие колебания наблюдаются в реальных биологических системах, однако, центр – не грубое стационарное состояние и исчезает при сколь угодно малом изменении параметров . Таким образом, незатухающие стационарные колебания в биологических системах, очевидно, имеют более сложную природу и не могут быть описаны в рамках линейных моделей.

Завершая анализ системы двух линейных дифференциальных уравнений, остановимся на понятии бифуркации и бифуркационной диаграммы.

Как мы убедились, качественное поведение системы (4.18) зависит от собственных значений матрицы рассматриваемой системы, определяемых формулой (4.20).

Рассмотрим плоскость параметров и найдем области, соответствующие каждому из пяти типов грубых стационарных состояний. Каждой паре собственных значений матрицы А соответствует определенная точка плоскости параметров . Связь между типами стационарных состояний и характером собственных значений представлена в табл. 4.2.

Таблица 4.2

			Тип стационарного состояния
	, ,		неустойчивый узел
	, ,		устойчивый узел
	,		седло
	,		неустойчивый фокус
	,		устойчивый фокус
			центр

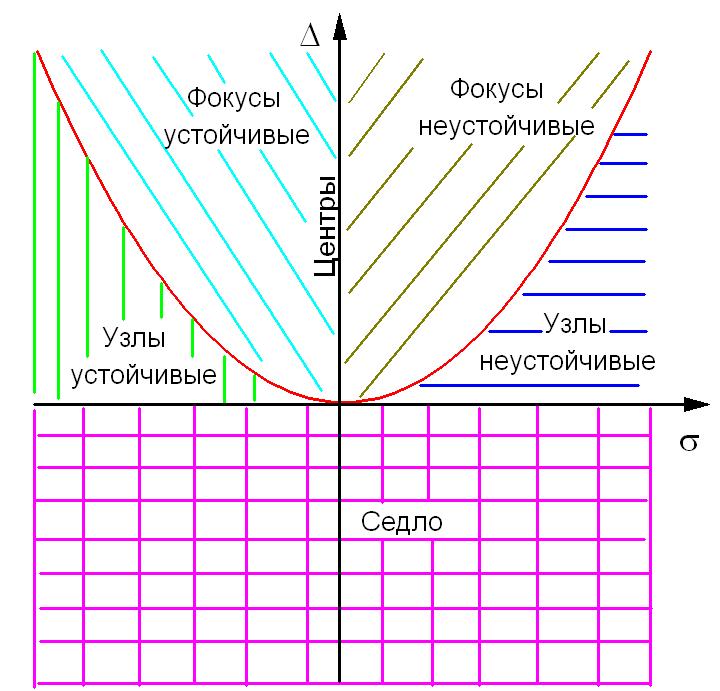
Рис. 4.11. Диаграмма разбиения плоскости (σ,Δ) на области, соответствующие различным типам ст.с. Уравнение параболы Δ = σ2/4

Отметим, что грубым стационарным состояниям соответствуют области плоскости , ограниченные некоторыми кривыми, в то время как не грубому стационарному состоянию – центру, соответствует луч .

На рис. 4.11 приведены построенные области с качественно различным поведением рассматриваемой системы (4.18). Это построение называется бифуркационной диаграммой. Кривые, разделяющие области с качественно различным поведением системы, называются бифуркационными кривыми. Явление качественного изменения поведения системы при непрерывном переходе через бифуркационную кривую из одной области в другую называется бифуркацией. На бифуркационной диаграмме (рис. 4.10) хорошо видно, из каких грубых стационарных состояний в какие можно перейти, непрерывно меняя параметры и (мы не рассматриваем вырожденную точку ). Так, седловая точка через бифуркацию может превратиться в устойчивый или неустойчивый узел, а затем соответственно в устойчивый или неустойчивый фокус. Устойчивый фокус может превратиться в неустойчивый и, наоборот, проходя через центр.

Аналогичным образом может быть классифицирован произвольный -мерный случай линейных систем. Грубые стационарные состояния могут быть описаны следующим образом.

1. Все корни действительны и больше нуля – неустойчивый узел.

2. Все корни действительны и меньше нуля – устойчивый узел.

3. Все корни действительны, не равны нулю и разных знаков – различные разновидности седла.

4. Имеются комплексные корни и все действительные части корней отрицательны – различные виды устойчивого фокуса.

5. Имеются комплексные корни и среди действительных частей корней есть положительные – различные виды неустойчивого фокуса.

Более точная классификация с учетом негрубых стационарных состояний основывается на жордановом представлении матрицы системы (4.18).

Подробно рассмотрев линейный случай, перейдем к нелинейным системам. Так же, как и в рассмотренном примере одного нелинейного дифференциального уравнения, основной подход заключается в линеаризации системы нелинейных уравнений в окрестности стационарной точки, т.е. система (4.16) в окрестности стационарной точки представляется в виде:

( 4.22)

где , – бесконечно малые функции второго порядка в окрестности точки ; , , , .

Будем говорить, что система линейных уравнений (4.18) простая, если , т.е. среди собственных значений матрицы нет нулевых.

Стационарная точка системы (4.22), для которой , называется простой.

Имеет место фундаментальная теорема о линеаризации.

Теорема 4.1. Пусть нелинейная система (4.16) имеет простую стационарную точку . Тогда в окрестности этой точки фазовые портреты самой системы (4.16) и соответствующей линеаризованной системы качественно эквивалентны, если только неподвижная точка линеаризованной системы не является центром.

Таким образом, если собственные значения линеаризованной системы имеют действительную часть, отличную от нуля, то фазовые портреты нелинейной системы и ее линеаризации качественно эквивалентны в окрестности стационарной точки. Такие стационарные точки называются гиперболическими.

Для линейного случая, если выполняется условие , стационарное состояние единственно и локальный фазовый портрет определяет глобальный фазовый портрет системы.

Если все стационарные точки нелинейной системы простые, можем ли мы, зная локальные фазовые портреты в окрестности каждой из стационарных точек, построить глобальный фазовый портрет системы? Ответ на этот вопрос в общем случае отрицательный. В частности, помимо стационарных точек на плоскости возникают предельные циклы.

Дадим формальное определение предельного цикла: замкнутая траектория на фазовом портрете называется предельным циклом, если она изолирована от всех остальных замкнутых траекторий, точнее, если существует трубчатая окрестность, не содержащая других замкнутых траекторий.

Существует три типа предельных циклов:

а) устойчивый (притягивающий) предельный цикл или аттрактор, где траектории навиваются на предельный цикл с обеих сторон при .

б) неустойчивый (отталкивающий) предельный цикл или репеллер, где траектории удаляются от предельного цикла при с обеих сторон.

в) полуустойчивый предельный цикл, где траектории с одной стороны навиваются на него и с другой стороны удаляются.

Заметим, что внутри предельного цикла на плоскости всегда существует хотя бы одна стационарная точка. Предельный цикл не может быть получен как следствие локального анализа стационарных точек.

Мы уже говорили о бифуркациях – явлении, при котором происходит качественное изменение типа стационарной точки. Непрерывное изменение параметров свойственно для многих реальных систем. Предельный цикл может появиться в результате бифуркации рождения цикла или, как ее часто называют, бифуркации Хопфа (или более правильно Андронова-Хопфа). Сформулируем следующую фундаментальную теорему.

Теорема 4.2. Пусть система ОДУ с параметром

( 4.23)

имеет стационарную точку в начале координат при всех значениях действительного параметра . Пусть собственные значения и соответствующей линеаризованной системы чисто мнимые при . Если и (0,0) – асимптотически устойчивая стационарная точка при , то 1) точка бифуркации, 2) существует интервал такой, что для любого точка (0,0) – устойчивый фокус, 3) существует интервал такой, что для любого точка (0,0) – неустойчивый фокус, окруженный предельным циклом, размер которого увеличивается с ростом .

Заметим, что, если для систем второго порядка по существу имеется полная теория качественного поведения решения системы, то уже для систем третьего порядка возникают принципиально новые явления, такие, как динамический хаос и странные аттракторы и их теория далека от своего завершения.