Уравнение Ферхюльста (логистическое уравнение)

В качестве примера изложенного подхода рассмотрим так называемое логистическое уравнение или уравнение Ферхюльста, предложенное в 1838 году. Логистическое уравнение описывает единственную гомогенную популяцию особей, соревнующихся за ресурсы, чьё количество ограничено. Современное экспериментальное обоснование этого уравнения относится к области микробиологии, где исходные предположения оказываются наиболее естественными. Исследования такого рода активно проводились в первой половине ХХ века.

В частности, была изучена динамика популяции дрожжей Saccharomyces Cervesia (пивные дрожжи) в растворе сахара. Эксперимент начинается с малого количества дрожжей и в начальной стадии их количество возрастало по экспоненте. Позднее количество сахара уменьшилось и дрожжи начинали конкурировать за ресурсы (сахар). Вторым компонентом конкурентной борьбы может быть отравление дрожжей алкоголем.

Так как рассматриваемая модель хорошо известна и достаточна проста, то мы опишем её очень кратко.

Состояние системы в данный момент времени мы будем описывать концентрацией дрожжей . В системе одновременно протекают два процесса: рождение и смерть. Из-за конкуренции за ресурсы (сахар) скорость рождения уменьшается, а скорость смерти возрастает при увеличении размера популяции. Простейшим предположением являются линейные зависимости:

(4.8)

где – скорость рождения, – скорость смерти. Так как

,

то, введя обозначения , , получим следующую модель

. (4.9)

Полученное уравнение называется логистическим уравнением или уравнением Ферхюльста (или логистическим уравнением с непрерывным временем). Конечно, это крайне упрощённая модель, однако, в определённой области параметров она довольно неплохо аппроксимирует экспериментальные результаты. Логистическое уравнение (4.9) легко решается аналитически:

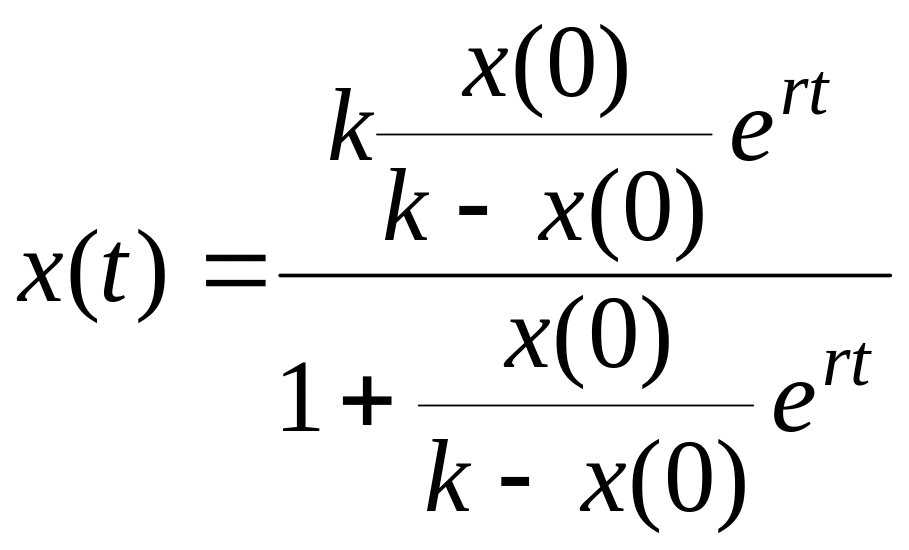, (4.10)

Из уравнения (4.9) легко находятся стационарные точки и . Мы будем рассматривать случай , что соответствует модели, в которой скорость рождения больше скорости смерти в отсутствии конкуренции (избыток ресурсов). Из следует, что и . Рассмотрим устойчивость этих стационарных точек. Для этого в соответствии с изложенной теорией рассмотрим знак производной

. (4.11)

При имеем (так как ) и стационарная точка неустойчива. При имеем и так как стационарная точка устойчива. Качественное поведение кинетических кривых может быть описано следующим образом: если , то монотонно убывающая функция, асимптотически стремящаяся к ; если , то монотонно возрастающая функция без точек перегиба, асимптотически стремящаяся к ; если , то монотонно возрастающая функция с точкой перегиба. Соответствующие кинетические кривые показаны на рис. 4.3.

Популяционная модель с дискретным временем

Теперь рассмотрим аналогичную модель популяции, но с дискретным временем. Дискретность времени в динамике популяций возникает достаточно естественно: сезонность размножения, световой цикл в течении суток и т.д.

Достаточно общий вид уравнения с дискретным временем может быть записан как

, (4.12)

где – численность популяции в -й момент времени и т.д.; – некоторая функция.

Рис. 4.3. Кинетические кривые уравнения Ферхюльста при различных начальных условиях х(0). Время t и объем популяции х в условных единицах.

Простейший вид уравнение (4.12) принимает в случае, если численность каждого следующего поколения в популяции зависит только от численности предыдущего поколения. Это справедливо для многих видов насекомых, а также некоторых видов рыб, птиц и зоопланктона. Можно сказать, что в этом случае поколения не перекрываются во времени. Уравнение (4.12) принимает следующий вид:

. (4.13)

Удивительно, что даже это простейшее уравнение демонстрирует исключительно разнообразное поведение: монотонность; затухающие колебания; незатухающие колебания с различным периодом; динамический хаос.

В качестве примера приведём дискретное логистическое уравнение, отталкиваясь от непрерывного уравнения (4.9). Заменив на , где , , получим дискретный аналог уравнения (4.9):

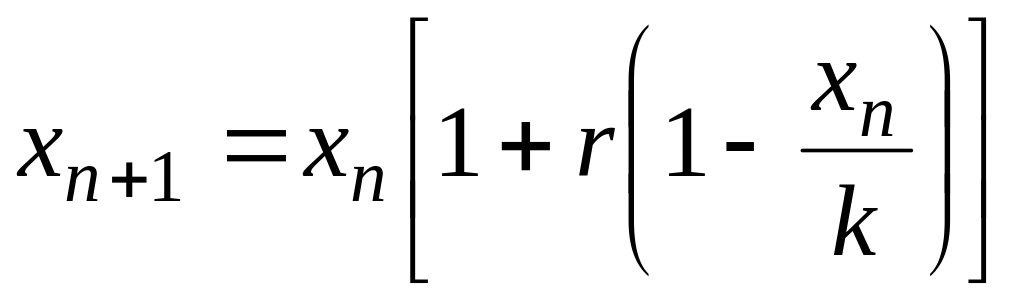, (4.14)

Полученное уравнение, корректное с математической точки зрения, некорректно с биологической точки зрения, так как, если , то из уравнения (4.14) следует, что . У непрерывного уравнения Ферхюльста этот недостаток отсутствует. Чтобы от него избавиться, необходимо модифицировать правую часть уравнения (4.14). Одна из возможных модификаций была предложена для численности популяции насекомых и рыб:

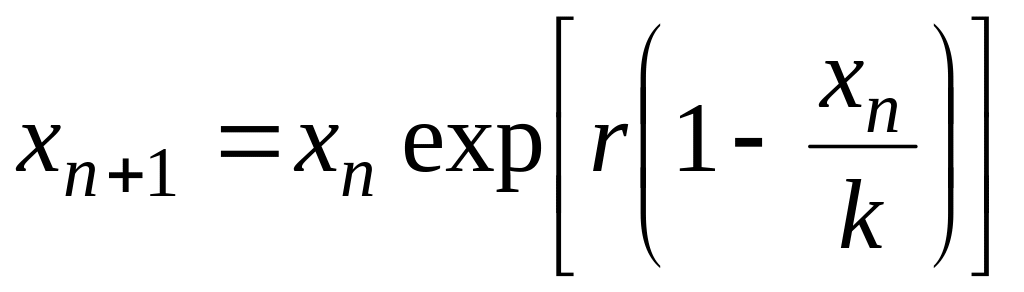. (4.15)

Для этого уравнения (4.15) существует устойчивое стационарное состояние при . Значения стремятся к нему монотонно при . При мы видим затухающее колебания. При возникают двухточечные циклы. При последовательно появляются циклы периода При появляется динамический хаос. Заметим, что численные значения и являются приближёнными.

Аналогичными свойствами обладает и исходная модель (4.14) при несколько других значениях концов интервалов. Подобное поведение называется каскадом бифуркаций удвоения периода.

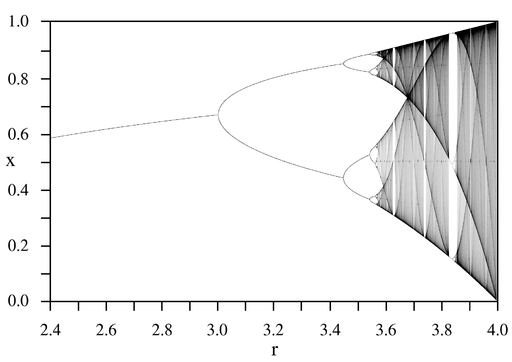
В качестве примера на рис. 4.4 приведена бифуркационная диаграмма классического логистического отображения. По оси абсцисс отложено значение параметра , а по оси ординат – значение при . При значения отображения расходятся при любых начальных значениях.

Рис. 4.4. Бифуркационная диаграмма классического логистического отображения

В настоящее время вопрос о том, наблюдается ли обсуждаемое хаотическое поведение в реальных экологических системах, остаётся открытым. Основная проблема состоит в том, что в подавляющем большинстве экологических систем существуют сильные стохастические возмущения (погода, температура и т.д.). По этой причине практически невозможно понять, является ли хаотичность данных следствием нерегулярных возмущений или следствием хаотической динамики. В искусственно созданных популяциях насекомых, в которых очень жестко поддерживались постоянные условия, удалось показать, что динамический хаос действительно имеет место в экологических системах и не только качественно, но и количественно описывается соответствующими уравнениями.

Рассмотрим теперь более сложные экологические системы, для описания которых требуется более чем одна переменная. Общая теория таких систем хорошо разработана для случая двух переменных, к рассмотрению которого мы и переходим.

Вообще, динамика популяций, которую мы начали рассматривать, является классическим объектом биоматематики и математического моделирования в биологии. Идеи, высказанные Лоткой и Вольтеррой в первой половине ХХ века и знаменитый пример с кроликами и лисами, являются основой для изучения взаимодействия различных биологических видов или отдельных субъектов. Отметим одно принципиальное отличие биологических систем от физических. В физических системах значительную роль играют всевозможные симметрии и законы сохранения (массы, энергии, импульсов и т.д.), что существенно облегчает описание протекающих процессов. В биологии, к сожалению, это не так и мощные методы, разработанные в физике, не могут быть использованы при исследовании биологических систем без их существенного модифицирования.