Глава 4. Математическое моделирование в биологии

Данная глава завершает наше пособие. Поэтому помимо вопросов, непосредственно относящихся к биологии, мы сформулируем ряд общих требований к математическим моделям с учетом уже изложенного материала.

В биологии (и не только) применяются модели двух типов: модели данных и модели систем. Определение этих типов в приложении к биологии дано в журналах «American Journal of Phisiology» и « Journal of Applied Phisiology».

«Модели данных – это модели, которые не требуют, не используют и не отображают каких-либо гипотез о физических процессах (системах), в которых эти данные получены». Так, типичными моделями данных являются статистические модели. Среди уже рассмотренных примеров несложно выделить модели данных (например, модель, описывающая олимпийские рекорды в беге на 200м).

Модели систем (системные модели) «строятся в основном на базе физических законов и гипотез о том, как система структурирована, и возможно о том, как она функционирует». Чаще всего системные модели в биологии описываются системами дифференциальных уравнений, как обыкновенных, так и в частных производных, которые могут дополняться алгебраическими уравнениями.

Мы и ранее затрагивали вопросы, связанные с адекватностью моделей. Рассмотрим теперь этот вопрос более подробно. Обычно под адекватностью понимается «достаточное соответствие» модели и моделируемого объекта. Как уже говорилось, наилучшей модели не существует. Всё на самом деле зависит от исходной задачи, которая была поставлена. С точки зрения практических приложений не так важно, насколько близко математическое описание соответствует физике реальной жизни. Таким образом, степень близости модели своему физическому (биологическому, химическому и т.д.) прототипу не является критерием адекватности, а лишь следствием выбранного подхода.

В первой главе мы обсуждали знаменитые модели, описывающие сценарий «ядерной зимы». Оценить степень «физической» близости этих моделей и реальных процессов в мире вряд ли возможно, так как моделируемые процессы плохо изучены и количество параметров, взятых по принципу «правдоподобия», очень велико. Однако своей задаче – сообщить человечеству масштабы возможной катастрофы – эта модель вполне адекватна.

С учетом накопленного опыта перечислим еще ряд свойств моделей, которые свойственны моделям биологических систем, однако не являются специфическими и относятся к моделям во всех отраслях науки и техники.

Первая особенность, которую следует отметить, заключается в том, что модель не обнаруживает новое явление, а лишь предсказывает его. (Довольно распространено заблуждение, что модель позволяет обнаруживать качественно новые явления). Действительно, всё, что найдено в модели, требует своего экспериментального подтверждения. Исключением здесь являются разве что модели типа моделей «ядерной зимы», экспериментальное подтверждение которых по очевидным причинам исключено.

Вторая особенность заключается в том, что объяснение, даваемое моделью, может быть неединственным. Это означает, что модель не позволяет различить две или более гипотез. Приведём следующий пример.

В природе широко распространены нематоды или круглые черви (Nematoda) – тип первичнополостных червей, насчитывающий в настоящее время около 80 тысяч известных видов. Вообще по оценкам специалистов, примерно 900 тысяч видов еще неизвестно науке. Размеры нематод колеблются (у различных видов) от 80 микронов до 8 метров. Свободноживущая нематода Caenorhabditis elegans длиной около 1 миллиметра с 1974 года является модельным объектом в молекулярной биологии, биологии развития и нейрофизиологии (рис. 4.1).

Рис. 4.1. Свободноживущая нематода Caenorhabditis elegans

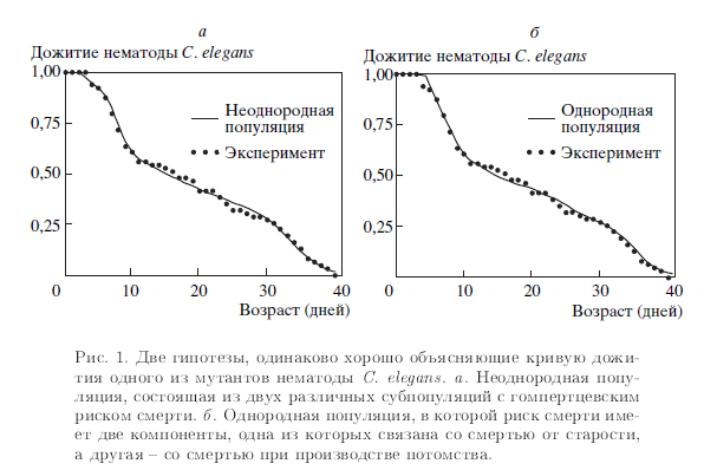
В связи с этим её геном полностью просеквенирован первым среди всех многоклеточных организмов в 1998 году. В частности, C. elegans имеет одну из самых простых нервных систем. Взрослая гермафродитная особь состоит из 959 клеток и имеет всего 302 нейрона, связи между которыми были полностью описаны. Некоторые мутанты этой нематоды обладают сложной кривой дожития (рис. 4.2). Две модели, основанные на принципиально различных гипотезах, дают практически совпадающие результаты, и определить, какая из двух гипотез справедлива на основе моделирования представляется невозможным.

Дожитие нематоды C. elegans
Возраст (дней)
(а)		(б)
Рис. 4.2. Две гипотезы, одинаково хорошо объясняющие кривую дожития одного из мутантов нематоды C. Elegans. (а) Неоднородная популяция, состоящая из двух различных субпопуляций с гомпертцевским риском смерти; (б) Однородная популяция, в которой риск смерти имеет две компоненты, одна из которых связана со смертью от старости, а другая – со смертью при производстве потомства

В одной гипотезе предполагается, что исходная популяция состоит из двух субпопуляций, коротко– и долгоживущей. Первая субпопуляция вымирает примерно к 15 дню, а вторая – к 42 дню. В другой гипотезе предполагается, что популяция генетически однородна, однако, риск смерти определяется двумя компонентами, одна связана со старением, а вторая – с процессом репродукции.

Ещё одна особенность моделирования заключается в сужении пространства возможных объяснений. Так, в демографии для описания зависимости риска смерти организмов от возраста с начала 19 века используется простое уравнение Гомпертца

, (4.1)

где – риск смерти; – коэффициенты Гомпертца; – коэффициент Мейхена, учитывающий риск смерти независимо от возраста.

Вообще демографические процессы весьма сложны, так как напрямую связаны с социальными сдвигами, развитием науки и т.д. Поэтому достаточно очевидно, что уравнение (4.1) не может в полной мере отразить всю их специфику.

Приведём любопытный пример. Обработка демографических материалов на большом временном интервале (1850-1950 годы) показывает отрицательную корреляцию между коэффициентами и (корреляция Стрелкера-Милдвана) и долгое время рассматривалась как один из незыблемых демографических законов (правда, не получив объяснения). Однако, начиная с 1950 года всякая корреляция между и исчезла. Причина, естественно, в том, что уравнение (4.1) слишком простое и корреляция между и оказалась артефактом модели.

Ещё один известный недостаток биологических моделей (связанный в первую очередь со сложностью моделируемых объектов и процессов) относится к моделям данных. Даже сильная корреляция не означает ещё наличие причинно-следственной связи. Корреляция может вытекать из того, что коррелируемые величины являются различными следствиями одной и той же общей причины. Заметим также, что в некотором диапазоне параметров правильно воспроизвести наблюдаемое явление может модель, построенная на ошибочных представлениях. Особенно это характерно для моделей, содержащих значительное количество «подгоночных» параметров. В хорошей модели количество таких параметров минимально.

Мы уже рассмотрели кратко пример несоответствия простой модели реальному процессу. Для биологических систем это характерное явление. В частности, во многих случаях более реалистические модели требуют междисциплинарного подхода (этот факт характерен и для моделей в области нанотехнологии, так как сама нанотехнология – междисциплинарная наука).

Рассмотрим более подробно один из первых примеров такого рода. Попытка моделирования острых отравлений на языке стандартной фармакокинетики натолкнулась на непреодолимые трудности. Действительно, классическая модель фармакокинетики рассматривает организм как несколько различных, изолированных друг от друга зон и вводимое лекарство распределяется по ним независимо от дозы. Если же вместо лекарства мы будем рассматривать яд, то такая модель справедлива только для его малых концентраций, что абсолютно неинтересно при модели отравления, связанной с большими дозами. Классическая фармакокинетика здесь неприменима в принципе, так как яд выводится из организма системами, свойства которых под его действием изменяются в худшую сторону. Таким образом, здесь модель фармакокинетики должна быть дополнена моделями физиологии, учитывающими физиологическое действие яда.

На этом мы закончим вводное описание математического моделирования в биологии. Самое существенное, что следует подчеркнуть, заключается в следующем: сложность и недостаточная изученность биологических систем; широкий спектр объектов и процессов, от молекул и конформаций до нейрофизиологии, популяционной биологии и демографии.

С учётом сказанного мы приведём лишь несколько классических моделей, ибо, как писал Козьма Прутков, «нельзя объять необъятное».

Исторически первые математические модели в биологии (включая демографические) возникли ещё в конце 18 в начале 19 веков. Наиболее известная модель такого рода – это знаменитый закон Мальтуса об экспоненциальном росте народонаселения и линейном росте производства продуктов питания. Однако, настоящий расцвет математическая биология переживает, начиная со второй четверти ХХ века. В первую очередь, это связано с именами Лотки и Вольтерры, построивших и изучивших первые современные модели популяционной биологии.