Метод бисекций

После локализации корня (этот шаг необходим для сходимости большинства методов) производится вычисление значения функции на границах исходного интервала . Если значения имеют различные знаки, то вычисляем значение функции , где , и сравниваем знак со знаками . Очевидно, что длина интервала, на котором находится искомый корень, уменьшается в два раза. Алгоритм метода бисекций сводится к выполнению следующих действий:

1. Вычисляем , где .

2. Если одного знака с , в качестве исходного выбирается интервал , если разного знака, то выбирается интервал 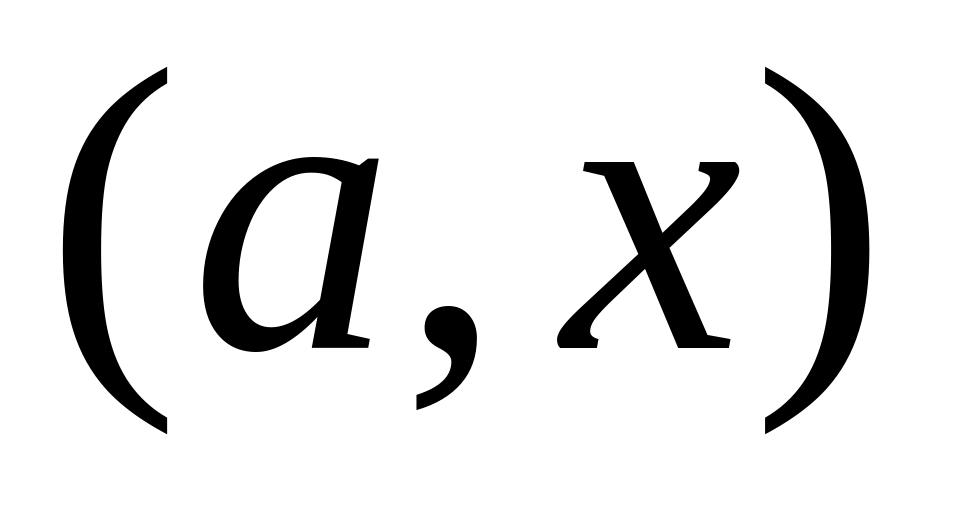, далее возврат к шагу 1).

Вычисления продолжаются до тех пор, пока не достигается требуемая точность, которую в данном случае можно определить как , где – длина исходного интервала , – количество шагов итерации.

Достоинством метода бисекций является его универсальность, а основным недостатком – медленная сходимость.

Наиболее часто используемым является метод Ньютона-Рафсона (Newton-Ruphson).

Метод Ньютона

Метод Ньютона основан (как и многие другие вычислительные алгоритмы) на разложении функции в ряд Тейлора в окрестности начального приближения к точному значению корня

(3.10)

Сохраняя только первых два слагаемых в левой части разложения (3.10), получаем уточненное значение корня

. (3.11)

Так как ряд Тейлора (3.10) мы обрезали, оставив только два слагаемых, значение , вычисленное по формуле (3.11), снова является приближением.

Полученный алгоритм называется методом Ньютона-Рафсона и имеет вид:

. (3.12)

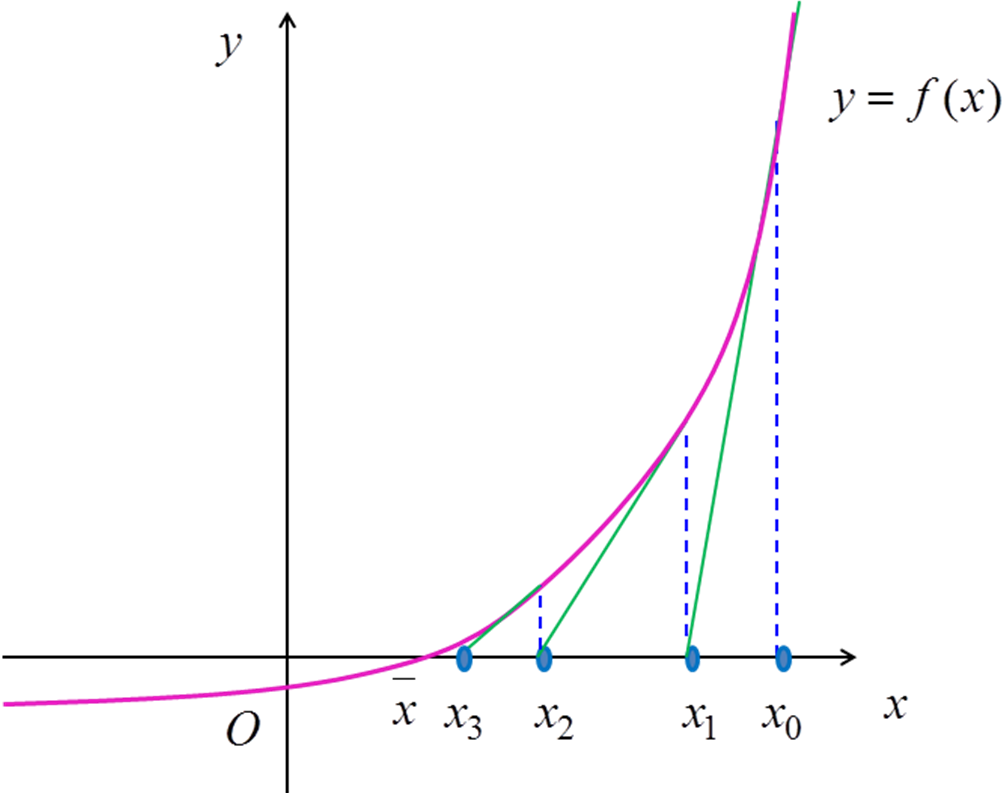
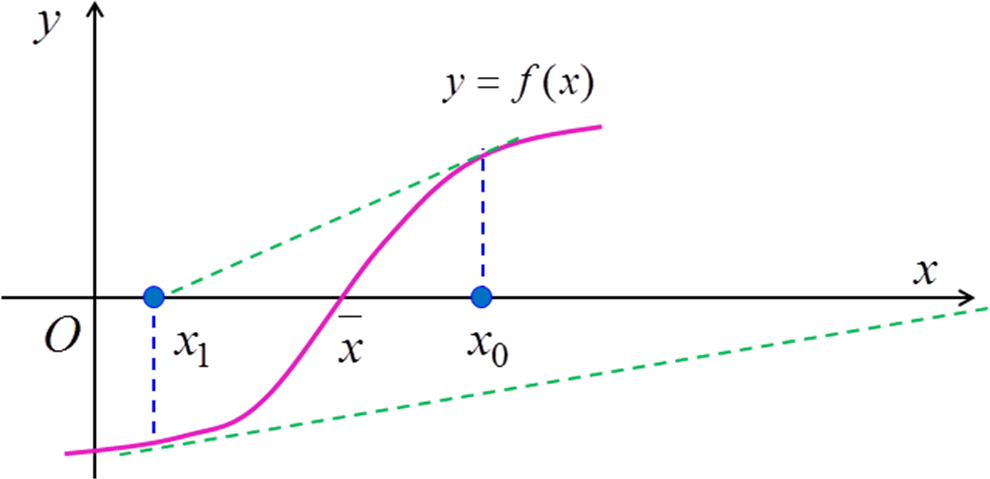
Графическая иллюстрация метода Ньютона-Рафсона показана на рис. 3.2. Изложенный алгоритм не всегда сходится (рис. 3.3).

Рис. 3.2. Сходящийся метод Ньютона-Рафсона	Рис. 3.3. Расходящийся метод Ньютона-Рафсона

Достаточное, но необходимое условие сходимости метода Ньютона-Рафсона может быть сформулировано следующим образом: если знакопостоянны в интервале , имеют одинаковый знак, итерационная последовательность (3.12) всегда сходится к точному значению корня .

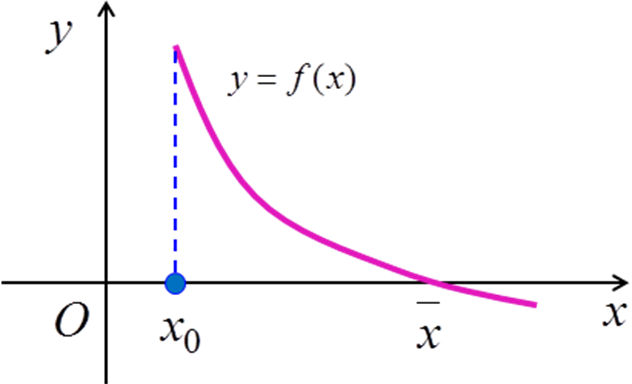
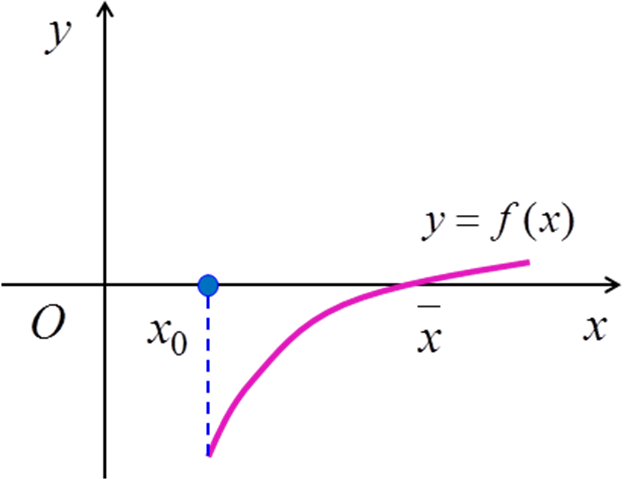
Например, если , , , то последовательность (3.12) сходится к точному корню (рис. 3.4), аналогично, случай , , показан на рис. 3.5.

Более точным методом, основанным на разложении (3.10) является метод Ньютона второго порядка. Для построения этого алгоритма сохраняют три члена в левой части (3.10). В результате получаем следующее уравнение для уточненного значения корня:

Рис. 3.4	Рис. 3.5

.

Отсюда получаем итерационную формулу метода Ньютона:

. (3.14)

Выбор знака «+» или «–» в формуле (3.14) определяется близостью значения к нулю.

Определение молярного объема реального газа

В качестве примера использования метода Ньютона-Рафсона рассмотрим задачу об определении молярного объема реального газа при заданной температуре и давлении. Будем считать, что газ подчиняется уравнению Соава–Редлиха–Квонга (3.2). Параметры определяются через критическую температуру и критическое давление газа:

, . (3.15)

Переменная является эмпирической функцией температуры

, (3.16)

где – фактор эксцентричности газа, .

Для н-бутана константы уравнения Соава–Редлиха–Квонга (3.2) следующие: К, кПа, , универсальная газовая постоянная Дж/кмоль·К.

Для решения поставленной задачи перепишем уравнение (3.2) в виде кубического уравнения (3.3) относительного коэффициента сжимаемости .

Из физических соображений в качестве начального значения выбираем (значение коэффициента сжимаемости для идеального газа).

Выше критической температуры уравнение состояния Соава–Редлиха–Квонга имеет единственный действительный корень, локализованный вблизи значения , вытекающего из уравнения состояния идеального газа Клапейрона-Менделеева.

Метод бисекций и метод Ньютона-Рафсона являются универсальными и могут быть использованы при решении произвольных нелинейных уравнений. Очень часто в приложении возникают полиномиальные уравнения (например, уравнение Соава–Редлиха–Квонга), для решения которых существуют специфические методы, позволяющие найти не только действительные, но и комплексные корни (знание комплексных корней полинома необходимо, в частности, при решении систем линейных дифференциальных уравнений n-го порядка).

Одним из таких специфических подходов является сведение задачи определения корней полинома к задаче определения собственных значений некоторой матрицы. Для нахождения собственных значений матриц существуют универсальные алгоритмы, которые быстро сходятся.

Можно показать, что определение корней полинома

(3.17)

сводится к вычислению собственных значений матрицы

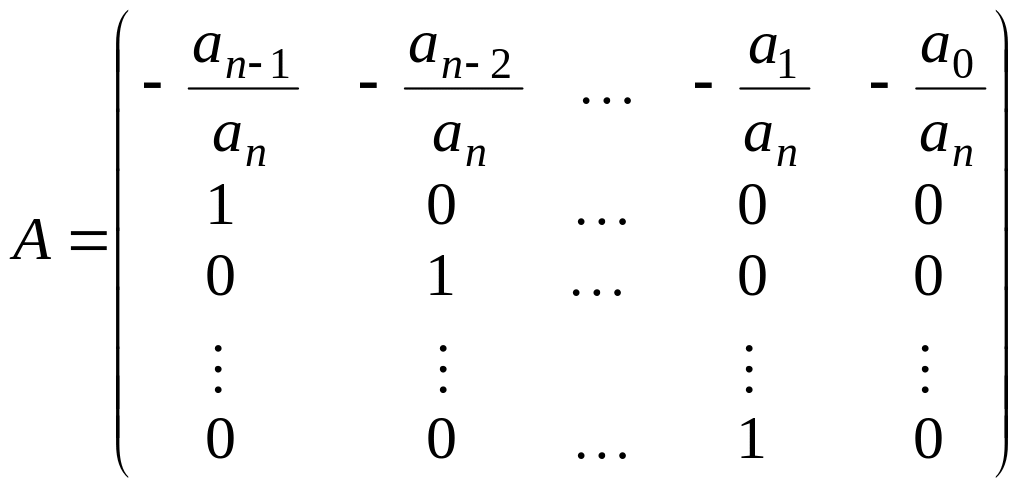. (3.18)

С вычислительной точки зрения, задача вычисления собственных значений матрицы значительно более устойчивая, чем задача вычисления корней полинома, особенно высокой степени.

В качестве еще одной модели, которая требует решения нелинейного уравнения (в данном случае это трансцендентное уравнение относительно молярного объема) рассмотрим уравнение состояния реального газа Бенедикта-Вебба-Рубина:

, (3.19)

где , и – константы.

Если давление измеряется в атмосферах, объем – в литрах/моль и температура – в кельвинах, то значения констант уравнения (3.19) для н-бутана будут равны: , , , , , , , .