Нелинейные уравнения
Рассмотрим два базовых метода, пригодных для решения любых нелинейных уравнений: метод бисекций и метод Ньютона-Рафсона, а также более подробно проанализируем нюансы применения этих вычислительных методов к полиномиальным уравнениям.
Любое нелинейное уравнение может быть представлено в виде:
,
(3.4)
а в частном случае полиномиального уравнения как
.
(3.5)
Корни уравнения (3.5) могут быть:
а) действительные с кратностью, равной 1,
б) действительные с кратностью, больше 1,
в) комплексно-сопряженные,
г) любые комбинации перечисленных возможностей.
Действительная часть корней может быть положительной, отрицательной или равной нулю.
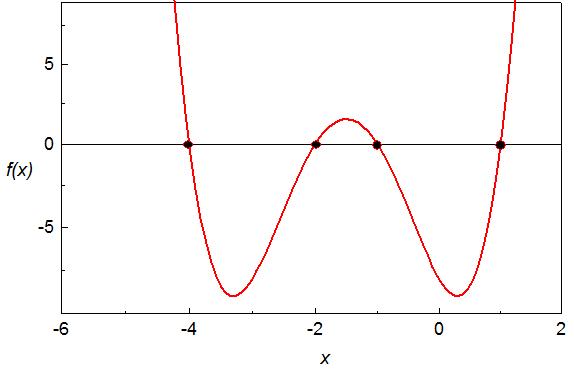
На рис. 3.1 представлены различные возможности на примере полиномов четвертой степени:
а)
имеет четыре действительных корня
кратности 1,
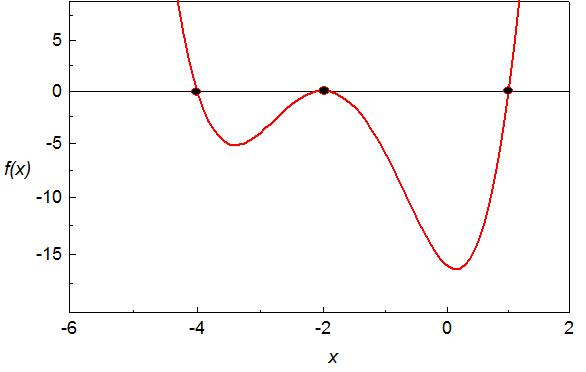
б)
имеет два действительных корня кратности
1 и действительный корень кратности 2,
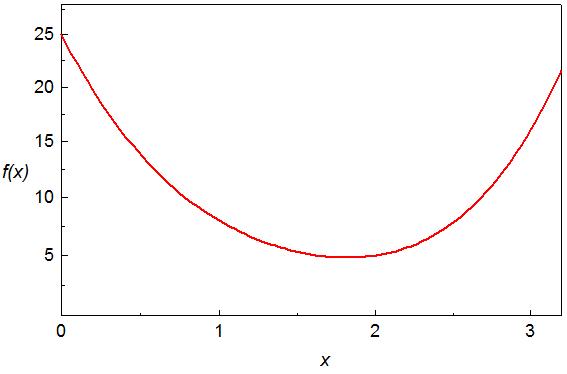
в)
имеет две пары комплексно-сопряженных
корней,
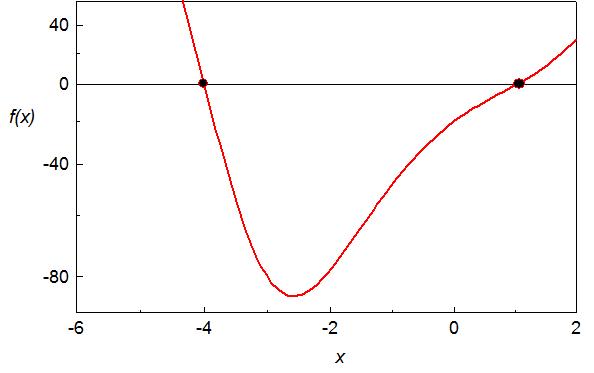
г)
имеет два действительных корня кратности
1 и пару комплексно-сопряженных корней.
а)
|
б)
|
в)
|
г)
|
Рис. 3.1. Заполненные кружки показывают точки пересечения графика функции f(x) осью Ox, абсцисса которых являются действительными корнями уравнения f(x)=0
|
|
Остановимся несколько подробнее на корнях кратности больше 1.
Пусть
– корень уравнения (3.4) кратности
.
Тогда в точке
,
очевидно, будут выполняться следующие
соотношения:
.
(3.6)
Соотношения (3.6) очень часто используются при поиске кратных корней.
Второй особенностью кратных корней является их неустойчивость относительно малых шевелений функции. Действительно, рассмотрим простейший случай сдвига функции по оси .
Пусть
для простоты
– корень кратности 2. Тогда
и
.
Рассмотрим уравнение
,
где
– сколь угодно малая величина, и найдем
его приближенное решение в окрестности
точки
.
Будем искать корень в виде
.
Отметим, что
может быть комплексным. Тогда
(3.7)
с точностью до членов второго порядка.
Так
как
и
,
то
.
Отсюда получаем
и
.
Таким
образом, при малом сдвиге функции
по оси
из одного корня
кратности 2 мы получаем два корня
кратности 1:
;
если
,
то пару комплексно-сопряженных корней;
если
,
то два различных действительных корня.
То, что получившиеся корни не кратные,
легко проверяется при помощи разложения
в точке
до членов первого
порядка по
.
Посмотрев на график полинома б) на рис.
3.1 легко визуально убедиться в
справедливости полученного результата.
Повторив
те же самые выкладки для корня кратности
,
получим аналогичный результат, т.е.
корней кратности 1.
Мы показали, что кратные корни нестабильны относительно малых шевелений функции . Стабильность некратных корней доказывается аналогично.
Этот результат очень важен с точки зрения приложений. Вкратце его можно сформулировать следующим образом: кратных корней в природе не бывает.
Кратные корни возникают только в приближенных математических моделях. Приведем простую аналогию. Уравнение обычного идеального осциллятора имеет вид:
.
(3.8)
Это
уравнение описывает незатухающие
гармонические колебания с частотой
.
Если в правую часть уравнения (3.8) подставим гармоническую силу, изменяющуюся с той же частотой :
,
то амплитуда колебания начинает неограниченно возрастать. Это явление хорошо известно и называется резонансом.
На самом деле, в любой реальной системе максимальная амплитуда колебания оказывается ограниченной. Причины могут быть различными, однако все они с формальной точки зрения сводятся к тому, что уравнение идеального осциллятора является приближенным уравнением и при больших амплитудах колебаний перестает корректно описывать реальный процесс. Читатели, знакомые с радиотехникой, знают понятие добротности резонатора, по которой как раз определяют максимальную амплитуду колебаний на резонансной частоте.
Исходя из проведенного анализа, мы не будем останавливаться на алгоритме нахождения кратных корней, а сосредоточим свое внимание на простых корнях нелинейных уравнений.
Наиболее эффективный метод нахождения корней нелинейных уравнений заключается в применении того или иного итерационного процесса, который начинается в некоторой точке недалеко от значения корня и сходится к нему с требуемой точностью за конечное число шагов.
Базовые подходы к нахождению действительных корней нелинейного уравнения существенно меняются по мере развития вычислительной техники и программного обеспечения. По-видимому, самый простой и эффективный современный метод локализации корней, а зачастую и их определения с достаточной степенью точности – графический (новое – это хорошо забытое старое). В любом пакете, позволяющем строить графики функций, таком, как Excel, Origin, Mathlab и т.д., строится график непрерывной функции в некотором априорно заданном интервале (в случае необходимости производится его корректировка). Визуально определяется примерное положение корней, а затем интервал построения графика уменьшается до тех пор, пока положение корня не будет найдено с требуемой точностью. По существу излагаемый подход эквивалентен (только быстрее сходится) методу бисекций.
Рассмотрим несколько стандартных методов определения корней.