Эквивалентность мрг и модели Изинга

Теперь остановимся на эквивалентности МРГ и модели Изинга. Эта эквивалентность легко устанавливается при помощи замены переменных:

, (2.64)

где – классический спин, принимающий значения +1.

Подставив выражение (2.64) в формулу для эффективного гамильтониана (2.51) и отбрасывая несущественные слагаемые, получим гамильтониан модели Изинга в магнитном поле:

, (2.65)

где J – энергия взаимодействия двух соседних классических спинов; h – энергия взаимодействия классических спинов с внешним магнитным полем.

Это очень важное обстоятельство, позволяющее переносить результаты, полученные в рамках одной модели, на другую модель.

Применение метода Монте-Карло при исследовании двумерной мрг

Для численного исследования МРГ ввиду ее важности разработано много различных методов. В настоящее время, по-видимому, наиболее важным и универсальным является метод Монте-Карло. Отметим, что здесь выступает характерная черта процесса моделирования – одну и ту же модель можно изучить при помощи различных математических методов, а математический метод, в свою очередь, может быть реализован при помощи различных вычислительных алгоритмов.

Рассмотрим применение метода Монте-Карло к исследованию построенной модели для случая d=2.

Метод Монте-Карло по своей сути является стохастическим (вероятностным) методом и одним из базовых вопросов при его реализации является генерирование случайных чисел. Настоящие случайные числа высокого качества могут быть получены с использованием физических эффектов, таких, как, например, белый шум, возникающий вследствие термических возбуждений в полупроводниковом диоде. Однако, при реальных вычислениях обычно используются специальные алгоритмы, генерирующие псевдослучайные числа, которые имеют статистические свойства, аналогичные настоящим случайным числам. Большинство генераторов псевдослучайных чисел основано на некоторой итерационной процедуре:

. (2.66)

Используя 32 битные целые числа, мы можем получить различных числа и, следовательно, период итерационной процедуры (2.66) не превышает . Одним из простейших алгоритмов генерации является следующее линейное отображение:

(2.67)

c максимальным периодом .

Больший период может быть получен, если случайное число зависит от большого количества предшественников. Функция вида

, (2.68)

используя 32 битные целые числа, имеет максимальный период . Отметим, что при и генерировании одного миллиона чисел в секунду, период преобразования (2.68) составит 584942 года. Случайные числа очень высокого качества могут быть получены при помощи следующего алгоритма:

а) ,

Эта последовательность имеет период .

б) имеет период .

Период их комбинации равен .

Стандартный генератор псевдослучайных чисел воспроизводит с определенной точностью равномерное распределение. Чтобы получить другие распределения, используют соответствующие преобразования исходного равномерного распределения. В частности, для получения нормального распределения используется известный метод Бокса-Муллера:

(2.69)

Где метод Монте-Карло наиболее востребован?

Многие физические задачи включают в себе вычисление интегралов очень высокой размерности. Например, интегралы по траекториям (квантовая механика) или более привычное нам термодинамическое усреднение.

Рассмотрим более подробно использование метода Монте-Карло для вычисления термодинамических средних. Здесь и далее мы будем рассматривать введенную выше простейшую модель решеточного газа.

Если нас интересует только термодинамика системы, то для решения поставленной задачи используется так называемый алгоритм Метрополиса.

Заметим, что моделирование динамики решеточных систем существенно более сложная задача и здесь мы ее рассматривать не будем.

Сформулируем алгоритм построения изотерм адсорбции для рассматриваемой простейшей модели решеточного газа:

а) Возьмем квадратную решетку узлов и введем периодические граничные условия по каждой из координат. (Периодические граничные условия минимизируют влияние конечности размера системы.) Фактически мы рассматриваем решетку на торе.

б) Зададим параметры модели, т.е. значения величин и .

в) Зададим начальное распределение частиц на решетке. Обычно в качестве начального распределения выбирается либо пустая решетка, либо распределение частиц, сформулированное на предшествующем шаге моделирования.

г) Будем рассматривать возможное изменение состояния системы как марковский процесс, при котором за один шаг изменяется состояние не более чем одного узла.

д) Процесс изменения состояния решетки на каждом шагу описывается алгоритмом Метрополиса (1953 год), который для рассматриваемой модели приобретает следующий вид:

(i) Случайным образом выбирается узел на решетке.

(ii) Рассматривается возможность изменения состояния избранного узла. Для этого вычисляется возможное изменение термодинамического гамильтониана. Для нашей модели при переходе от незаполненного узла к заполненному имеем

, (2.70)

где – число ближайших соседей.

При переходе от заполненного узла к незаполненному узлу:

. (2.71)

(iii) Если , то попытка принимается и происходит изменение системы.

(iv) Если , то вычисляется величина

(2.72)

и вычисляется случайное число .

(v) Если , то попытка принимается, если , то отвергается.

(vi) Возврат к пункту (i).

Единицей измерения условного времени в методе Монте-Карло служит шаг Монте-Карло – это число попыток, удачных или неудачных, равное .

Для алгоритма Метрополиса строго доказано, что в результате выполнения достаточно большого количества шагов (i)–(vi) система приходит к термодинамическому равновесию. Отметим, что алгоритм Метрополиса не описывает реальной динамики прихода к равновесию и, строго говоря, не может быть использован при моделировании неравновесных систем. Для этой цели разработан более сложный алгоритм в рамках так называемого кинетического метода Монте-Карло.

Определение момента достижения равновесия – очень непростая задача, не имеющая однозначного решения в рамках излагаемого подхода. Самая сложная проблема – отличить истинное равновесие от метастабильного состояния с большим временем жизни. В значительной степени этот вопрос решается на «глаз». Количество Монте-Карловских шагов (МКШ), необходимых для достижения термодинамического равновесия, сильно зависит от исследуемой системы и колеблется от до МКШ. В настоящее время в связи с развитием вычислительной техники по умолчанию выполняется не менее МКШ.

Характерный размер решетки (в ряде случаев требуются экстремально большие размеры), однако, в некоторых случаях можно использовать и меньшие размеры.

После прихода системы к равновесию для вычисления средних термодинамических характеристик необходимо проводить усреднение по состояниям системы. Обычно предполагается, что корреляции в состоянии системы исчезают после МКШ, т.е. через каждые 30 МКШ состояния системы считаются статистически независимыми.

Более точное определение (при необходимости) времени релаксации системы – достаточное затратное дело. Таким образом, при вычислении средних характеристик системы после достижения термодинамических характеристик через каждые 30 МКШ вычисляется интересующая нас величина (в данном случае степень покрытия), а затем производится обычное усреднение:

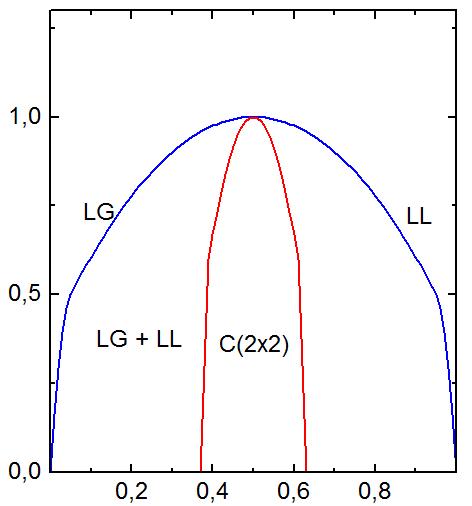
Рис. 2.11. Фазовая диаграмма для квадратной решетки при отталкивании и притяжении ближайших соседей

, (2.73)

где – количество МКШ, по которым осуществляется усреднение.

Более тонкие вопросы, связанные, например, с построением фазовой диаграммы системы, для своего решения требуют более развитых методов, такие как метод «взвешивания» для определения точки фазового перехода первого рода или метод кумулянтов Биндера для фазовых переходов второго рода.

Для простой модели решеточного газа, которую мы рассматриваем, фазовая диаграмма весьма проста и приведена на рис. 2.11.

Если (притяжение), то в системе происходят процессы конденсации с образованием плотной фазы (переход решеточного газа в решеточную жидкость). При этом происходит фазовый переход первого рода, что проявляется появлением вертикальных участков на изотерме (рис. 2.12).

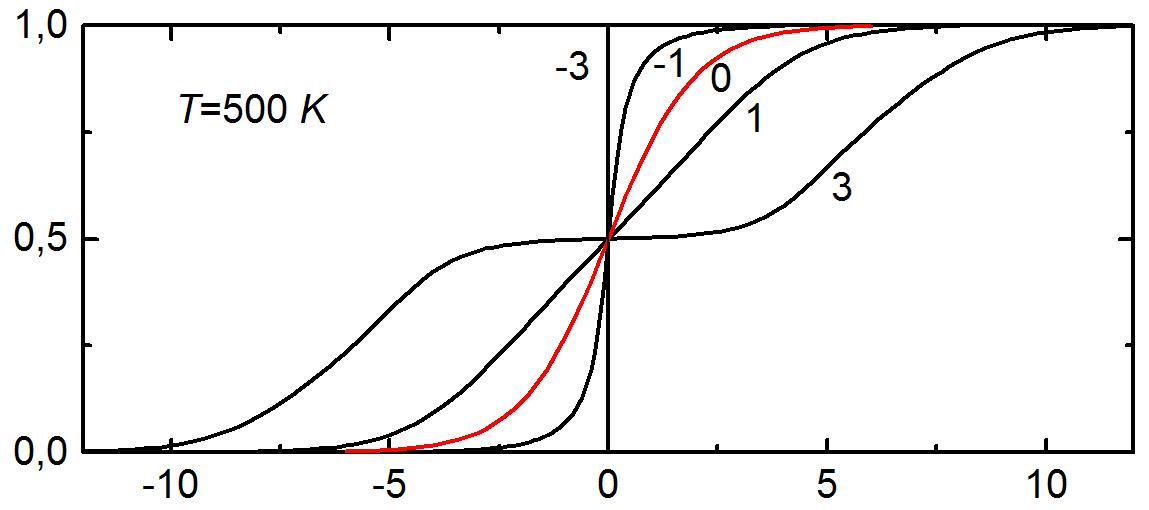
Рис. 2.12. Изотермы для квадратной решетки с учетом взаимодействий только ближайших соседей. Энергия латеральных взаимодействий (в ккал/моль), температура Т (в кельвинах) показаны на рисунке

Если (отталкивание), то в системе возникает упорядоченная фаза со структурой – «шахматная доска». Это происходит фазовый переход второго рода.

Образование стабильной упорядоченной структуры проявляется появлением «плато» на изотерме (рис. 2.12).

Завершая изложение нашего примера отметим, что для двумерных систем метод трансфер-матрицы и метод Монте-Карло очень хорошо дополняют друг друга.