Применение метода трансфер-матрицы при исследовании одномерной мрг

Для одномерной системы, как уже говорилось, возможно точное вычисление большой статистической суммы.

Мы будем использовать метод трансфер-матрицы.

Рассмотрим цепочку, состоящую из N узлов и введем периодические граничные условия, т.е. будем полагать, что . Тогда, вводя безразмерные энергию и химический потенциал

, (2.56)

получим

. (2.57)

Экспонента в формуле (2.57) может быть представлена в виде произведения сомножителей, значение которых зависят только от состояния соседних узлов:

. (2.58)

Отталкиваясь от соотношения (2.58), после несложных выкладок, получаем одно из основных соотношений метода трансфер-матрицы:

, (2.59)

где Tr означает взятие следа матрицы, Т – трансфер-матрица размера , имеющая следующий вид:

. (2.60)

Переходя к пределу при , легко получим выражение для большого термодинамического потенциала, приходящегося на один узел решётки,

, (2.61)

где – наибольшее по модулю собственное значение трансфер-матрицы Т.

Формула (2.61) является основной при конкретном применении метода трансфер-матрицы.

При исследовании любой одномерной решеточной системы вначале строится трансфер-матрица размера , где – количество возможных состояний узла решетки (в нашем случае , узел либо занят, либо свободен). Далее вычисляем ее наибольшее собственное значение и вычисляем большой термодинамический потенциал, а потом по стандартным термодинамическим выражениям всю термодинамику системы. Заметим, что элементы трансфер-матрицы положительны и, быть может, нулевые.

Для трансфер-матрицы оказывается справедливо следующее утверждение: наибольшее по модулю собственное значение трансфер-матрицы единственно и положительно. Это утверждение есть следствие теоремы Перрона-Фробениуса. Следовательно, в основном соотношении метода (2.61) можно убрать знак модуля.

Применим изложенные результаты к нашей модели.

Из (2.60) найдем наибольшее собственное значение матрицы Т:

. (2.62)

Из (2.62) для получаем точное уравнение изотермы:

. (2.63)

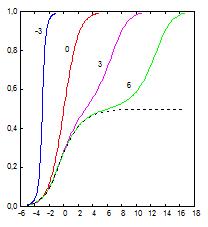
Степень покрытия	Безразмерный химический потенциал
Рис. 2.10. Изотермы одномерной МРГ при различных значениях . Значения показаны на рисунке числами. Пунктирная линия соответствует

Семейство изотерм одномерной МРГ при различных значениях показано на рис. 2.10. Изотерма при является классической изотермой Ленгмюра.

Как уже говорилось, для исследуемой модели при d=1 метод трансфер-матрицы дает точное аналитическое решение поставленной задачи.

Для приложений значительно больший интерес имеют двумерные и трехмерные модели. Так, наша модель при d=2 может служить простейшей моделью хемосорбции на гранях (100) металлов с гранецентрированной кубической решеткой (Pt, Pd, и т.д.) При d=3 эта модель описывает в первом приближении сплав меди и цинка, широко известный как латунь. Для размерности d > 1 метод трансфер-матрицы не позволяет получить точное, а тем более аналитическое решение, однако, может быть использован как мощный приближенный численный метод.