Классическая молекулярная динамика

Рассмотрим теперь более подробно классическую молекулярную динамику, с которой мы будем сталкиваться и далее в последующих главах пособия. Обычно при вычислении используются либо метод «прыжка лягушки», либо один из алгоритмов Верле.

Для системы без внутримолекулярных степеней свободы стандартный алгоритм Верле записывается в следующем виде:

(2.45)

Рассмотрим вопрос о граничных условиях и способах вычисления среднего давления. Чаще всего в молекулярной динамике используются периодические граничные условия, чтобы свести к минимуму внешние эффекты конечного размера системы. Недостатком этого подхода является трудность вычисления таких величин, как давление.

Рис. 2.6.

Для этой цели удобнее использовать другие граничные условия. Это так называемый ящик с упругими стенками (рис. 2.6). Такие граничные условия позволяют естественным образом вычислить давление.

Атомы моделируемой системы находятся в кубе с отражающими стенками, т.е. как только атом пересекает грань куба, нормальная компонента вектора скорости меняет свой знак. Таким образом, кинетическая энергия сохраняется, а импульс, равный , передается стенке.

Среднее изменение импульса в единицу времени может быть интерпретироваться как сила, действующая на стенку:

(2.46)

и, соответственно, для давления имеем

. (2.47)

В рамках метода Верле отражение легко описывается как изменение значения соответствующей координаты в моменты времен и .

Остается более подробно рассмотреть вопрос, связанный с начальным условием и введением температуры.

С самого начала распределим равномерно N частиц по эквивалентным позициям решетки, помещенной в куб. Начальные значения скорости задаются случайным образом в соответствии с распределением Максвелла (это специфический случай нормального распределения)

. (2.48)

Эффективная температура системы вычисляется из кинетической энергии системы в предположении равновестности системы

. (2.49)

Желаемая температура устанавливается при помощи процедуры перенормировки:

. (2.50)

Эта процедура используется несколько раз в процессе установления равновесия. Сглаживание процедуры достигается введением термостата

,

где – разумное время релаксации (обычно порядка 20 шагов по времени).

Применение метода молекулярной динамики при моделировании реальных систем

Рассмотрим теперь применение описанных подходов к моделированию реальных систем.

Современное развитие вычислительной техники позволяет моделировать динамику молекулярных систем, состоящих из десятков тысяч или даже миллионов частиц. Эффективность применения методов молекулярной динамики (МД) постоянно возрастает. Моделирование реальных физических систем, таких, как жидкости или кристаллы, а также гигантских биологических молекул на основе МД представляет собой генеральную линию развития теоретических исследований.

Самым нетривиальным моментом применения методов МД является выбор адекватных потенциалов взаимодействия. Наиболее сложный (с вычислительной точки зрения) аспект применения этого подхода связан с учетом электростатического взаимодействия. Для решения этой проблемы в США и Японии созданы специализированные процессоры. Отметим, что методы МД являются основой современной вычислительной биологии и их применение для этих целей будет рассмотрено в четвертой главе.

В соответствии с общей идеологией, сформулированной выше, прежде чем приступить к решению конкретной задачи, необходимо выяснить, существуют ли уже готовые и отлаженные пакеты. В задачах классического молекулярного моделирования этот вопрос особенно важен в связи со сложностью изучаемых моделей.

В настоящее время разработано довольно много пакетов, которые позволяют производить моделирование методами молекулярной динамики как пространственной структуры огромных биологических молекул, так и термодинамических систем, состоящих из большого количества сравнительно простых молекул. В качестве примера свободного программного обеспечения (ПО) приведем хорошо зарекомендовавшие себя пакеты AMBER и GROMOS. Заметим, что с математической точки зрения (см. вышеописанные алгоритмы Верле) методы МД не представляют особой сложности и их алгоритмическая реализация очень проста. Это означает, что исследователь ограничен только мощностью вычислительных средств, имеющихся в его распоряжении. Своей эффективностью эти методы обязаны тому факту, что в большинстве случаев квантово-механические эффекты значительно менее существенны, чем обычное электростатическое взаимодействие.

Главным недостатком классического метода молекулярной динамики является малый временной масштаб. Действительно, при учете внутримолекулярной динамики шаг по времени не должен превышать фс (напомним, что ). Если мы не учитываем внутримолекулярные колебания, шаг по времени может быть существенно увеличен до долей пикосекунды ( ). Отсюда следует, что временной интервал, на котором работают методы молекулярной динамики, не превышает нескольких наносекунд ( ), в то время как многие важные физико-химические и биологические процессы имеют характерные времена, достигающие секунд и часов.

Вопросы, связанные с использованием метода молекулярной динамики для изучения биологически важных молекул (белки, ДНК и т.д.), будут рассмотрены в четвертой главе, посвященной математическому моделированию в биологии. Здесь мы более подробно рассмотрим практически важный вопрос (традиционно относящийся к физике) о моделировании процессов нуклеации Ленард-Джонсовского пара в микропорах с твердыми стенками.

Многие физические процессы, определяемые термодинамикой (диффузия, нуклеация газов или жидкостей, вязкость и т.д.) в ограниченной области пространства, иногда начинают подчиняться совершенно иным закономерностям по сравнению с теми, которые характерны для свободного пространства.

Например, вода в зазоре толщиной в несколько молекулярных диаметров проявляет аномальную вязкость. Вообще свойства жидкостей, и в первую очередь воды, заключенной между двумя поверхностями, определяют многие важнейшие биологические процессы, диффузии газа или жидкости через мембраны (топливные элементы), играют значительную роль в аэрокосмическом и медицинском приборостроении, в проблемах смазки и т.д.

Поведение жидкости и газа в ограниченном пространстве (в условиях конфайтмента) – активно развивающаяся область науки.

Одним из ярких и практически важных примеров является нуклеация перенасыщенных паров между стенками и процессы капиллярной конденсации, в которых конфайтмент конденсированного газа изменяет термодинамические характеристики фазовых переходов. Заметим, что экспериментальное изучение роли конфайтмента – достаточно сложная задача.

Приведем результаты изучения конфайтмента на базе МД расчетов.

Изучалась гетерогенная нуклеация Ленард-Джонсовского перенасыщенного пара в нанопорах между двумя параллельными стенками. Одна из стенок предполагалась сильно адсорбирующей, вторая – слабо адсорбирующей. Бинарная смесь состояла из частиц-мишеней и газа-носителя, не участвующего в процессах нуклеации и конденсации.

На рис. 2.7 представлен визуалированный результат моделирования. Заметим, что в ряде случаев основным результатом МД-моделирования является именно визуальный образ.

Для моделирования пара и твердой стенки были использованы комбинации следующих потенциалов:

а) потенциал Ленарда-Джонса при , ,

Рис. 2.7. Процесс конденсации Ленард-Джонсовского пара в нанопоре между двумя твердыми стенками

б) сдерживающий гармонический потенциал при , .

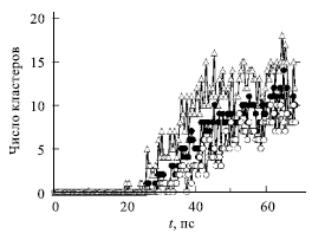
Некоторые результаты расчетов представлены на рис. 2.8.

Обнаружено, что степень гетерогенной нуклеации очень чувствительна к изменению параметров модели конденсирования пар-стенка и она на несколько порядков больше по сравнению со степенью однородной нуклеации при тех же параметрах.

При моделировании термодинамики сложных систем не менее важным методом, чем метод МД, является метод Монте-Карло.

Число кластеров

t, пс

Рис. 2.8. Степень нуклеации в гетерогенной системе пар-твердая поверхность: треугольники соответствуют n>25; заполненные кружки – n > 35; незаполненные кружки – n > 45