Метод Верле и метод «прыжка лягушки»

При использовании методов классической молекулярной динамики необходимо вычислять очень длинные траектории. По теореме Лиувилля фазовый объем классической системы из N взаимодействующих частиц сохраняется, поэтому крайне желательно использовать алгоритмы, которые удовлетворяют теореме Лиувилля.

Уравнения движения, которые являются системой ОДУ второго порядка,

запишем в стандартном виде системы ОДУ первого порядка, вводя обозначения:

, (2.27)

где и – функции времени и силы – функции координат, зависящих от времени. Перепишем уравнение (2.27) как

, (2.28)

где – оператор Лиувилля, действие которого описывается как

. (2.29)

Решение уравнения Лиувилля (2.28) формально может быть представлено как

. (2.30)

Для лучшего понимания дальнейших выкладок запишем несколько первых членов ряда Тейлора для экспоненты в (2.30):

, (2.31)

, (2.32)

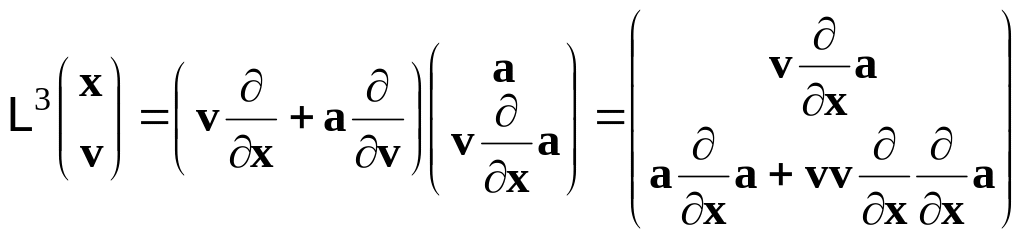. (2.33)

Так как

, (2.34)

, (2.35)

то с учетом (2.31)–(2.35) получим

. (2.36)

Метод Верле и метод «прыжка лягушки» базируются на достаточно общем подходе, связанном с упрощением структуры выражения .

Введем шаг по времени , где число шагов велико. Запишем очевидное равенство:

.

Теперь разобьем оператор Лиувилля на две части

.

Сложность выражения непосредственно связана с тем, что операторы и не коммутируют, т.е. . Следовательно,

.

Однако, при малых можно использовать приближенное равенство

, (2.37)

которое тем точнее, чем меньше .

Рассмотрим действие каждого из сомножителей в правой части (2.37):

.

Каждый из сомножителей правой части (2.37) осуществляет либо сдвиг по координате с постоянной скоростью , либо сдвиг по скорости с постоянным ускорением . По существу замена выражения на произведение в некотором смысле аналогична замене точного приращения функции ее линейной частью.

Перейдем теперь к изложению вычислительных алгоритмов.

Начнем с методов Верле.

Разложение для можно симметризовать:

( 2.38)

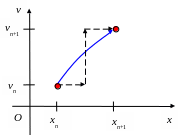
Соответствующий алгоритм называется позиционным алгоритмом Верле:

,

, (2.39)

.

Суть этого алгоритма схематически показан на рис. 2.3.

Если в (2.38) мы поменяем местами операторы и , сохранив симметризованную форму, то получим:

( 2.40)

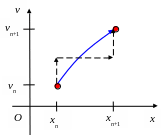
Это представление порождает так называемый алгоритм скоростей Верле

,

, (2.41)

.

Суть этого метода изображена на рис. 2.4.

Рис. 2.3. Позиционный алгоритм Верле	Рис. 2.4. Алгоритм скоростей Верле

Опишем теперь стандартный алгоритм Верле, который эквивалентен алгоритму скоростей:

(2.42)

Стандартный алгоритм Верле начинается с задания двух множеств координат и , алгоритм скоростей Верле – с задания множества координат и скоростей . Два обсуждаемых алгоритма дают одну и ту же траекторию, если положить .

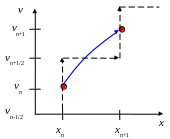
Рассмотрим еще один метод, тесно связанный с методом Верле. Это так называемый «leapfrog method». В русскоязычной литературе он известен под несколькими названиями: «прыжок лягушки», «чехарды», «перешагивания».

Этот метод основывается на простейшем разложении

, ( 2.43)

но вводятся две различных временных сетки для координат и скоростей, сдвинутых относительно друг друга на . Алгоритм записывается как

(2.44)

Рис. 2.5. «Прыжок лягушки»

Графическая иллюстрация этого алгоритма представлена на рис. 2.5. Недостатком алгоритма «прыжка лягушки» является пониженная точность определения скорости.

Методы Верле и родственные им методы широко используются в классической молекулярной физике. Помимо этого, большинство из вас регулярно сталкивается с результатами их использования. Речь идет о компьютерных играх с анимацией. Движение объектов в игре почти всегда описывается при помощи рассмотренных нами алгоритмов. Чтобы убедиться в этом, достаточно зайти на любой форум разработчиков игр.