2.3. Метод молекулярной динамики
В
настоящее время классическая
молекулярная динамика превратилась
в один из самых мощных инструментов
изучения молекулярных систем. Сущность
этого подхода заключается в моделировании
системы
материальных точек массой
,
,
взаимодействующих между собой.
Взаимодействие
описывается при помощи потенциальной
функции
,
где
– радиус-векторы материальных точек.
Моделирование сводится к численному
решению классических уравнений движения:
(2.23)
где
,
,
– координаты
-й
частицы по осям
,
соответственно;
– проекции силы, действующей на
-ю
частицу, на ось
,
соответственно;
– время.
Затем производится усреднение вдоль траекторий, и на основе этого усреднения вычисляются необходимые термодинамические характеристики.
Основной проблемой при построении модели является выбор поля сил, т.е. потенциальной функции . В литературе можно найти большой выбор таких функций в зависимости от изучаемой системы. Мы рассмотрим только основные составляющие этих сил, которые являются общими практически для всех систем.
а) Внутримолекулярные силы
Внутримолекулярные степени свободы часто описываются в очень упрощенном виде с использованием понятия длины связи и угла между связями. Соответствующий вклад в общую потенциальную энергию можно тогда записать, используя внутренние координаты. Например, вклад в потенциальную энергию, связанный с изменением длины связи, может быть записан как
(гармоническое
приближение), (2.24)
где
– расстояние между
-й
и
-й
частицами, принадлежащими одной связи;
– равновесное расстояние между теми
же частицами;
– соответствующая силовая константа.
Аналогичные выражения могут быть записаны для членов, связанных с изменением углов.
Заметим, что экспериментальное определение силовых констант и им подобных осуществляется спектроскопическими методами, которые напрямую измеряют частоты внутримолекулярных колебаний.
б) Межмолекулярные силы
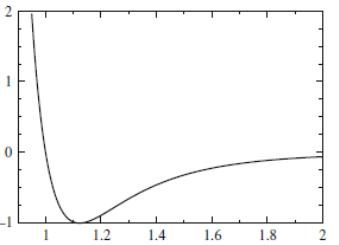
Отталкивание на малых расстояниях (следствие принципа Паули) и слабое притяжение на больших расстояниях (силы Ван-дер-Ваальса) – характерная черта любой молекулярной системы. Простейшей и часто используемой моделью является парный потенциал Ленарда-Джонса
,
(2.25)
где
– параметры модели;
– расстояние между молекулами.
Потенциал
Ленарда-Джонса изображен на рис. 2.2.
Положение минимума определяется
параметром
,
,
а минимальное значение энергии –
параметром
,
.
Распределение зарядов в молекулярных системах описывается через распределение мультиполей. Соответственно, электростатические взаимодействия описываются как взаимодействия заряд-заряд, заряд-диполь, диполь-дипольные взаимодействия и т.д. насколько это необходимо.
Если амплитуда внутримолекулярных колебаний мала, а это почти всегда выполняется для не слишком высоких температур, то колебательные и враща-
U/ε |
r/σ |
Рис. 2.2. Потенциал Ленарда-Джонса |
|
Опишем максимально упрощенную модель молекулярной системы без учета внутренних степеней свободы с полем сил Ван-дер-Ваальса. Эта модель достаточна адекватна для благородных газов, а также для разреженных газов, состоящих из неполярных небольших молекул, например, метана. Далее мы будем иметь в виду именно благородные газы. В этом случае сила, действующая на -й атом, определяется градиентом потенциала Ленарда-Джонса:
.
(2.26)
При вычислении термодинамических характеристик Ленарда-Джонсовского газа на первом этапе необходимо решить уравнение движения (2.23) с силой, определяемой (2.26) для достаточно большого количества атомов. Решение уравнений движения для большого количества частиц обычно осуществляется либо при помощи метода Верле (Verlet), либо метода «прыжка лягушки» (leapfrog method).
Дадим краткое описание этих методов.