9. Линейные ду высших порядков: основные определения, постановка задачи Коши.
11.Неоднородные ду II порядка: теорема о структуре общего решения.
Пусть имеем неоднородное линейное уравнение второго порядка
(1)
Теорема
о структуре общего решения 1. Общее
решение неоднородного уравнения
представляется как сумма какого-нибудь
частного решения этого уравнения у*
и общего решения
соответствующего однородного уравнения
(2)
Док-во. Доказать, что сумма
(3)
- общее решение неоднородного уравнения.
Подставим
в уравнение (1) вместо у:
(4)
Т.к. - решение уравнения (2), то
Т.к. у* - решение уравнения (1),
,
равенство (4) является тождеством. Т.о.
первая часть теоремы доказана.
Докажем,
что выражение (3) - общее решение уравнения
(1), т.е. докажем, что входящие в него
произвольные постоянные можно подобрать
так, чтобы удовлетворялись начальные
условия:
каковы
бы ни были числа x0,
у0
и
(x0
должно быть взято из области, где функции
a1,
а2,
f(x)
непрерывны).
Представим
где
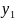и у2
- линейно независимые решения уравнения
(2), C1,
С2
- произвольные постоянные. Перепишем
равенство (3) в виде
Тогда
на основании начальных условий
Из этой системы уравнений нужно определить С1 и С2.
Определитель
этой системы - определитель Вронского
для функций y1
и у2
в точке х=х0.
Т.к. эти ф-ции по условию линейно
независимы, то определитель Вронского
такие
значения C1
и С2,
при которых формула (3) определяет решение
уравнения (1), удовлетворяющее данным
начальным условиям. Теорема доказана.
12.Линейные однородные ДУ II порядка с постоянными коэффициентами: характеристичес-кое уравнение, вид общего решения. Имеем линейное однородное уравнение 2-го порядка
(*)
где р и q - постоянные действительные числа. Найдем частные решения в виде
у = еkх, где k = const; тогда
Подставим в уравнение (*):
Т.к.
,
то,
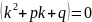- характеристическое уравнением по
отношению к уравнению (*).
Характеристическое уравнение есть квадратное уравнение, имеющее два корня: обозначим их k1 и k2.
Возможны
следующие случаи:
I.
k1
и k2
– действительные,
;
частные
решения:
Эти решения линейно независимы, т.к.
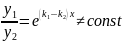
общее
решение имеет вид
II. k1 и k2 - комплексные числа;
Частные решения:
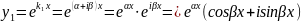
Общее решение:
(#)
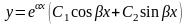Рассмотрим
случай, когда корни характеристического
уравнения чисто мнимые. При р=0,
уравнение (*) имеет вид
Характеристическое
уравнение принимает вид
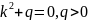
Корни характеристического уравнения
.
Решение (#) принимает вид
III.
k1
и k2
- действительные равные числа
.
Частные
решения:
,
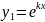Общее
решение:
.
13.Линейные неоднородные ДУ II порядка с постоянными коэффициентами: нахождения частного решения подбором по виду правой части уравнения. Пусть имеем уравнение
(*)
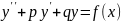где р и q - действительные числа.
Нахождение частного решения подбором по виду правой части уравнения. Если правая часть уравнения имеет следующий вид:
,
где
α
и β
- постоянные, Рn(х)
и Qm(х)
- многочлены от х
соответственно n-й
и m-й
степени, тогда частное решение уравнения
имеет вид:
r
= показателю кратности корня
в характеристическом уравнении
;
Rl(х)
и Tl(x)
- полные многочлены от х
степени l
с неопределенными коэффициентами,
.
.
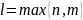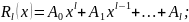
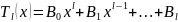Частные случаи f(x):
1)
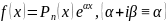
2)
,
A
– постоянная
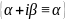
3)
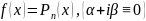
4)
5)
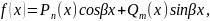
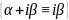
6)
,
.
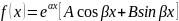Рассмотрим
первый частный случай:
.
Тогда возможны следующие случаи:
а) Число α не является корнем характеристического уравнения
. Тогда частное решение нужно искать в виде:
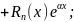
Дифференцируем:
Подставим
в (*):
-
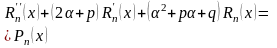
многочлен степени n
-
многочлен степени n-1
-
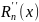многочлен степени n-2
Т.о., слева и справа от знака равенства стоят многочлены n-й степени. Приравнивая коэффициенты при одинаковых степенях х (число неизвестных коэффициентов = n+1), получим систему n+1 уравнений для определения неизвестных коэффициентов А0, А1, А2, ..., Аn.
б) Число α есть простой корень характеристического уравнения.
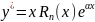
в) Число α - двукратный корень характеристического уравнения.
14. Системы ДУ: основные определения, система ДУ нормального типа, постановка задачи Коши. Ф-ии у1=у1(х), у2=у2(х),…, уn=уn(х) - удовлетворяют системе ДУ, содержащих аргумент х, искомые ф-ции у1, у2 , …, уn и их производные.
Рассмотрим систему уравнений первого порядка:
-
система нормального типа. Проинтегрировать
систему
- значит определить ф-ции у1,
у2,
…, уn,
удовлетворяющие системе уравнений
нормального типа и данным начальным
условиям:
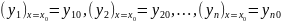
Рассмотрим нормальную систему трех уравнений с тремя неизвестными функциями: х=х(t), у=у(t), z=z(t).
Зададим
начальные условия:
.
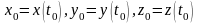Дифференцируем по t первое из уравнений:
Заменим производные их выражениями f1, f2, f3 из уравнений (*):
Дифференцируем и аналогично предыдущему, найдем:
Запишем систему:
Определим
ф-ии у=у(t),
z=z(t),
выразив их через х,
t
и производные
:
(#)
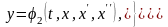Подставим эти выражения в последнее из уравнений, получим уравнение 3-го порядка для определения х=х(t):
.
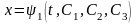Дифференцируя последнее выражение 2 раза, найдем производные как ф-ции от t, С1, С2, С3.
Подставляя эти ф-ии в уравнения (#), определим у(t), z(t):
Рассмотренный метод решения нормальных систем называется методом исключения.
Теорема Коши.
Пусть
функции
,
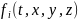i=1,
2, 3 непрерывны по всем переменным в
некоторой области D
и
имеют в этой области непрерывные частные
производные:
.
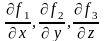Тогда каковы бы ни были значения
единственное
решение системы
,
удовлетворяющее начальным условиям
.