1.Задачи, приводящие к понятию дифференциального уравнения.

1. Равноускоренное движение. Пусть в начальный момент времени t=0 материальная точка имеет начальное положение S(0)=0, начальную скорость V(0)=V₀ и далее движется прямолинейно с постоянным ускорением a(t)=a. Если S(t) и V(t) – соответственно путь, пройденный точкой за время t, и ее скорость в момент времени t, то S′(t)=V(t) и V′(t)=a(t)=a. Т.е., ф-ция перемещения S(t) явл-ся решением диф.уравнения S′′(t)=a. Найдем решение, интегрируя уравнение дважды.

.

.

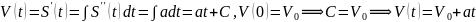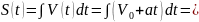
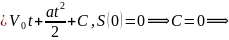
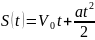2. Уравнение движения. Пусть материальная точка массы m движется прямолинейно под действием переменной силы F(t). Тогда в силу второго закона Ньютона . Поскольку a(t)=S′′(t), то ф-ция перемещения S(t) явл-ся решением диф.уравнения 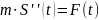. Это диф. уравнение называют уравнением движения. Например, если рассматривать свободное падение материальной точки в поле тяготения Земли, то действующая на точку сила сводится к силе тяжести F(t)=P=mg и уравнение движения имеет вид S′′(t)=g. Если полагать, что сила сопротивления воздушной среды пропорциональна скорости движения F_c(t)=kV(t), то суммарная сила, действующая на точку, равна F(t)=mg-F_c(t)=mg−kV(t). В этом случае уравнение движения имеет вид 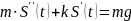. Его решением (для V₀=0) явл-ся ф-ция

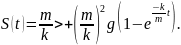
Скорость и ускорение такого движения изменяются так

3. Геометрические задачи. Пусть требуется найти линию, проходящую ч/з точку А(1,2) и обладающую следующим св-вом: для любой ее касательной отрезок этой касательной, заключенный м/у осями системы координат, в точке касания делится пополам. Обозначим ч/з y(x) уравнение искомой линии и пусть M(x₀,y₀) - ее произвольная фиксированная точка. Касательная к кривой в этой точке имеет уравнение y-y(x₀)=y’(x₀)(x-x₀). Найдем ординаты точек пересечения этой касательной с осями системы координат.

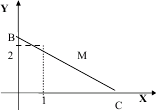
x_B=0, y_C=0. Тогда

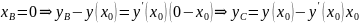
Т.к М – середина отрезка BC, то

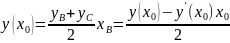
Отсюда

Т.к. x₀ - произвольная точка, то искомая ф-ция должна удовлетворять диф.уравнению первого порядка

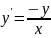
Для произвольной постоянной С ф-ция y(x)=C/x удовлетворяет этому уравнению. Т.к. кривая должна проходить ч/з точку А(1,2), то подставив в это решение x=1 и y=2, получим С=2. Решением явл-ся гипербола y=2/x.

2.Диф. уравнения первого порядка: основные определения, задача Коши, общее и частное решения, общий и частный интеграл. Диф. уравнение первого порядка имеет вид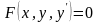 . (1)

Если (1) представима в виде y’=f(x,y) то ДУ разрешено относительно производной.

Задача Коши. Теорема о существовании и единственности решения ДУ. Если в уравнении y’=f(x,y) ф-ция f(x,y) и ее частная производная 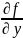по у непрерывны в некоторой области D на плоскости Оху, содержащей некоторую точку (х₀,у₀), то 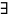единственное решение этого уравнения 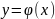, удовлетворяющее условию у₀=y(x₀).

Геометрический смысл теоремы: через точку (х₀, у₀) проходит единственная интегральная кривая (решение ДУ).

Условие, что при х = х0 функция у должна равняться заданному числу у0, называется начальным условием.

Общим решением ДУ первого порядка называется ф-ция :

1. она удовлетворяет ДУ при любом значении С; 2. 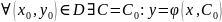удовлетворяет условие (х₀,у₀).

Равенство Ф(х,у,С)=0 называется общим интегралом ДУ.

Частным решением называется любая ф-ция 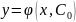которая получается из общего решения 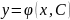, если в последнем произвольному постоянному С придать определенное значение С=С₀. Соотношение Ф(х,у,С₀)=0 называется частным интегралом ДУ.