Геометрическое распределение

Производится последовательность независимых испытаний, в каждом из которых возможно только 2 исхода

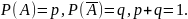
Испытания производятся до появления события А. Возможные значения случайной величины ξ : 1,..., m,...

вероятности этих значений определяются по формуле: (1.2.)

Геометрическим распределением называется распределение дискретной случайной величины ξ , определяемое формулой (1.2).

Геометрическое распределение имеет один параметр p.

Математическое ожидание и дисперсия этой случайной величины:

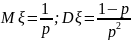
Вероятностный смысл параметра р – величина, обратная математическому ожиданию.

Название геометрическое распределение связано с тем, что вероятности образуют бесконечно убывающую геометрическую прогрессию со знаменателем q = 1− p .

13.Равномерное и показательное распределения.

Плотность распределения:

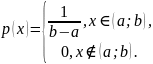
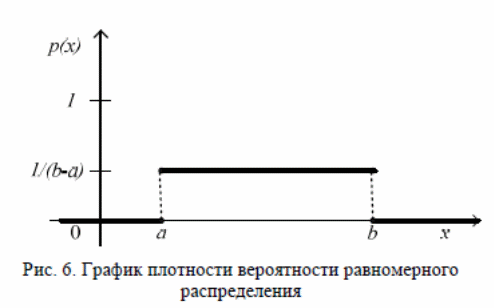
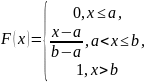
Равномерное распределение имеет два параметра a и b .

Математическое ожидание и дисперсия:

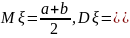
Показательным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

Показательное распределение имеет один параметр λ .

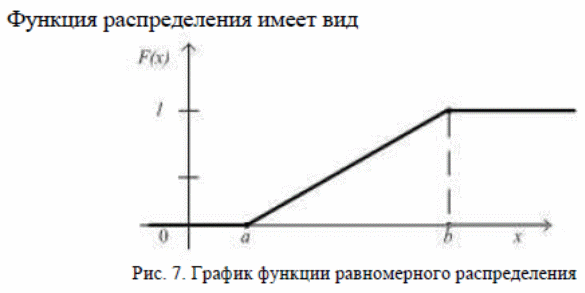
Функция распределения:

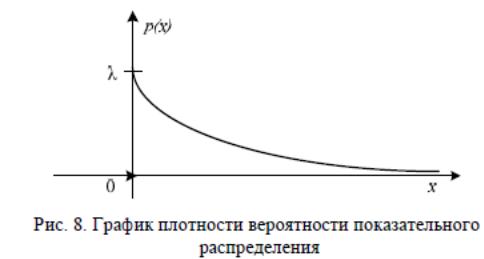
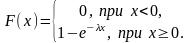
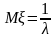
Характерным свойством показательного распределения является равенство математического ожидания и среднеквадратического отклонения: Mξ =σξ .

14.Нормальное распределение.

Нормальным (распределением Гаусса) называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

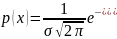
Нормальное распределение определятся двумя параметрами a и σ . Можно показать, что

Mξ = a, Dξ =σ² , σξ = σ .

При а=0 и σ=1 получим стандартное нормальное распределение:

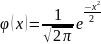
От произвольного нормального распределения можно перейти к стандартному с помощью преобразования

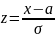
Функция стандартного нормального распределения имеет вид

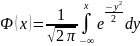
Функция 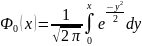называется функцией Лапласа.

Функции Ф₀ (x) и Ф(x) связаны между собой соотношением

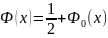
Вероятность попадания нормальной случайной величины в заданный интервал:

Вероятность заданного отклонения от математического ожидания для нормальной случайной величины

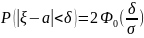
Покажем это

Преобразуем данную формулу, положив δ = σ ⋅ t . Получим

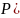
Если t=3, то ≈1

Правило трех сигм:

Если случайная величина распределена нормально, то с вероятностью, близкой к единице, абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

15.Закон больших чисел.

Случайная величина принимает значения, зависящие от многих причин, учесть которые не представляется возможным. Поэтому трудно предвидеть, какое значение примет она в результате опыта. Возникает вопрос, можно ли установить закономерности поведения для большого числа случайных величин. Закон больших чисел (ЗБЧ) показывает, что средний результат при достаточно большом количестве испытаний утрачивает случайный характер и может быть предсказан с достаточной точностью.

Для доказательства ЗБЧ рассмотрим неравенство Чебышева.