4. Условная вероятность. Независимость событий.

Часто при решений задач интересует вероятность появления события А, после того, как некоторое событие В уже произошло. Такую вероятность называют условной и обозначают P(A/B).

Определение 1 Условной вероятностью события А при условии, что событие В уже произошло называется

P(A/B)= , P(B)>0 (3.1)

Аналогично, условной вероятностью события B при условии, что событие A уже произошло называется :

P(B/A)= , P(A)>0 (3.2)

Из формул (3.1) и (3.2) следует теорема умножения:

P(AB)= 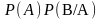= (3.3)

Вероятность произведения двух произвольных событий равна произведению вероятности одного из событий на условную вероятность второго, при условии, что первое уже произошло.

P(AB) = P(A)P(B / A) = P(B)P(A/ B) .

Распространим теорему умножения на конечное число событий

Вероятность совместного появления нескольких произвольных событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже произошли:

P(A₁ A₂ A_k)=P(A₁)P(A₂/A₁)*…*P(A_k/A₁A_{2 …}A_k-1)

Определение 2 События А и В называются независимыми, если вероятность произведения равна произведению вероятности этих событий.

P(AB)=P(A)P(B) (3.4)

Сравнивая (3.3) и (3.4) получим, что для независимых событий условные и безусловные вероятности совпадают.

P(A/B)=P(A)

Для конечного числа независимых событий вероятность произведения равна произведению вероятностей.

P(A₁A₂…A_k)=P(A₁)P(A₂)…P(A_K)

5. Формула полной вероятности. Формула Байеса.

Для удобства изложения материала рассмотрим следующий пример.

Пример 11. Имеется три одинаковые урны: в первой урне два белых и один черный шар; во второй – три белых и один черный; в третьей – два белых и два черных. Некто выбирает наугад одну из урн и вынимает из нее один шар. Какова вероятность того, что вынутый шар белый?

Проведение опыта возможно только в условиях исключающих друг друга гипотез (в нашем примере это случайный выбор любой из трех урн):

H₁, H₂,…, H_n (H_iH_j=∅ при i ≠ j) – 1.1

Гипотезы составляют полную группу несовместных событий с известными вероятностями появления P(H₁),P(H₂),…,P(H_n)

Рассматривается некоторое событие А, которое может появиться только вместе с одной из гипотез (1.1). Условные вероятности события А по каждой из гипотез заданы

P(A/H₁), P(A/H₂),…, P(A/H_n)

Задача состоит в том, чтобы вычислить вероятность события А. Для этого представим А как сумму n несовместных событий:

По правилу сложения вероятностей несовместных событий получаем

а по правилу умножения

P(H_iA)= P(H_i) P(A/H_i)

Откуда окончательно имеем

(1.2.)

Таким образом, безусловная вероятность события А в опыте с гипотетическими условиями вычисляется как сумма произведений вероятности каждой гипотезы на условную вероятность события при этой гипотезе.

Выражение (1.2) называется формулой полной вероятности. Она применяется во всех случаях, когда опыт со случайным исходом распадается на два этапа: на первом учитываются условия опыта, а на втором – его результат.

В рассматриваемом примере с урнами есть три гипотезы: H₁ – выбор первой урны с шарами; H₂ – второй урны; H₃ – третьей. Гипотезы представляют собой полную группу несовместных событий. Вероятности гипотез одинаковы и равны P(H₁)= P(H₂)= P(H₃)=1/3

Событие A = { появление белого шара} . Условные вероятности события А по каждой из гипотез соответственно равны

P(A/H₁)=2/3, P(A/H₂)=3/4, P(A/H₃)=1/2

По формуле (1.2) получаем вероятность вынуть белый шар

Иногда интересует, как перераспределятся вероятности гипотез после того, как событие А уже произошло: P(H_j/ A). По теореме умножения P(AH_j)=P(A)P(H_j/A)=P(H_j)P(A/H_j),

Подставляя в знаменатель формулу полной вероятности, получим формулы Байеса:

6. Схема независимых испытаний Бернулли.

При практических применениях теории вероятностей часто встречаются задачи, в которых один и тот же опыт или аналогичные опыты повторяются неоднократно. В результате каждого опыта может появиться или не появиться некоторое событие А. При этом нас интересует не результат каждого отдельного опыта, а общее число появлений события А в результате серии опытов. Например, если производится несколько выстрелов по одной и той же цели, то представляет интерес, как правило, не результат каждого выстрела, а общее число попаданий. В подобных задачах требуется определить вероятность любого заданного числа появлений события в результате серии опытов. Такие задачи решаются достаточно просто в случае, когда опыты являются независимыми.

Производится n независимых опытов, в каждом из которых может появиться или не появиться некоторое событие А, вероятность появления P(A) = p , а непоявления P( ) = q , при этом q = 1-p . Требуется найти вероятность Pn(m) того, что событие А в этих n опытах появиться ровно m раз.

Под элементарным событием в схеме Бернулли будем понимать последовательность наступлений и ненаступлений события А в n испытаниях. Обозначим А={1}, ={0}. Тогда элементарный исход можно представить в виде вектора, состоящего из нулей и единиц, например, (1,0,…, 1).

Найдем вероятность того, что в n испытаниях событие А появится ровно m раз.

Вычислим сначала вероятность того, что в 3-х испытаниях событие А появится два раза при условии, что вероятность наступления А в одном испытании равна p. При этом возможны следующие элементарные исходы: (1,1,0); (0,1,1); (1,0,1).

Вероятность каждого элементарного исхода одинакова и равна p²q. Таким образом, вероятность того, что в 3-х испытаниях событие наступит два раза Р₃(2)=3р²q.

Для произвольных m и n вероятность одного элементарного исхода равна p^mq^n-m. Число таких элементарных исходов равно числу способов разместить m единиц по n местам, а это по определению есть число сочетаний из n элементов по m. Таким образом, формула Бернулли имеет вид

Часто в схеме Бернулли интересует вероятность появления события А не ровно m раз, а от m₁ до m₂ раз включительно. Тогда она определяется формулой: