25.Проверка статистических гипотез.

Статистической гипотезой называется гипотеза о виде неизвестного распределения или о параметрах известного распределения.

Нулевой или основной называется выдвинутая гипотеза H₀ .

Конкурирующей или альтернативной называется гипотеза H₁ , которая противоречит нулевой.

Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное значение которой известно. Эту величину обозначают через χ² , если она распределена по закону «хи-квадрат», через Т – по за- кону Стьюдента, F – по закону Фишера и так далее.

В данном параграфе мы не принимаем во внимание распределение этой случайной величины, поэтому, в целях общности, обозначим ее через K.

Статистическим критерием называется случайная величина K, которая служит для проверки гипотезы H₀ .

Для проверки гипотезы по данным выборки (выборок) вычисляют частные значения входящих в критерий величин, и получают наблюдаемое значение критерия K_набл .

Значения статистического критерия, при которых H₀ принимают, называются областью принятия гипотезы. Значения критерия, при которых гипотезу H₀ отвергают, называется

критической областью. Точки, которые отделяют эти области, называют критическими.

Различают левостороннюю, правостороннюю и двустороннюю критические области.

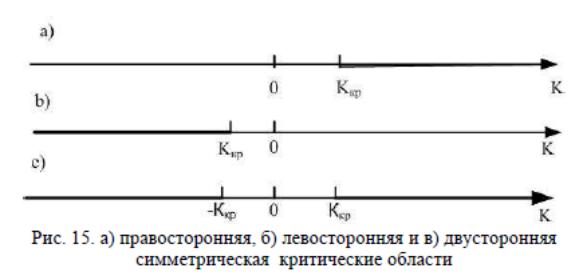
Правосторонней называется критическая область (рис.15, a), определяемая неравенством К>K_кр, K_кр> 0

Левосторонней называется критическая область (рис.15, б) определяемая неравенством К<K_кр, K_кр< 0

Односторонней называют правостороннюю или левостороннюю критическую область.

Двусторонней называется критическая область, определяемая неравенством

К<K`_кр, К< K^``_кр

В частности, если критические точки симметричны относительно нуля, то говорят о двусторонней симметрической критической области (рис. 15, с) |K|>K_кр, К_кр>0

При проверке статистических гипотез возможно возникновение ошибок.

Ошибка первого рода возникает, когда мы отвергаем правильную нулевую гипотезу. Вероятность совершить ошибку первого рода называется уровнем значимости и обозначается

α : P(H₁ /H₀ ) =α

Ошибка второго рода возникает, когда мы отвергаем правильную гипотезу H₁ . Вероятность совершить ошибку второго рода обозначается β : P(H₀ /H₁ ) = β

Величину ошибки первого и второго рода исследователь выбирает самостоятельно близкую к нулю: 0,01; 0,05; 0,001.

Отметим, что невозможно одновременно уменьшать ошибки первого и второго рода.

Проверка статистических гипотез осуществляется следующим образом:

1) по выборке вычисляется наблюдаемое значение критерия (К_набл);

2) если К_набл попало в критическую область, то нулевую гипотезу отвергают, а если в область принятия гипотезы, то говорят, что нет оснований отвергнуть гипотезу H₀ .

26. Критерий согласия Пирсона

Одной из основных задач математической статистики является установление закона распределения случайной величины на основании экспериментальных данных.

На практике о виде закона распределения можно судить по графику гистограммы. Параметры закона распределения обычно неизвестны и их заменяют на выборочные значения. Однако, как бы мы ни выбрали вид закона распределения и его параметры, полной уверенности в том, что мы получим истинный закон распределения, к которому принадлежит имеющаяся у нас выборка, не существует. Речь может идти лишь о том, что при определенном уровне значимости, выбранный нами закон согласуется с данными выборки.

Критерий проверки гипотезы о предполагаемом виде распределения называется критерием согласия. Наиболее распространенным из них является критерий согласия Пирсона или

критерий χ2 .

Пусть вид распределения изучаемого признака Х неизвестен и пусть есть основание предполагать, что он распределен по некоторой функции теоретического распределения F(x) . Сформулируем нулевую и альтернативную гипотезы. Пусть H₀ : Fn (x) = F(x), H₁ : Fn (x) ≠ F(x)

На основании данных выборки построим интервальный вариационный ряд. Для этого найдем:

1. x_min, x_max и размах варьирования R = x_max – x_min .

Весь интервал наблюдаемых значений Х разделим на k частичных интервалов (x_i,x_i+1) одинаковой длины, где k можно вычислить по формуле Стержеса k =3,32⋅ln n +1.

2. Подсчитаем эмпирические частоты n_i – число вариант, попавших в интервал (x_i,x_i+1)

3. Затем вычислим вероятности p_i попадания случайной величины в построенные интервалы, исходя из функции распределения F(x)

P_i = F (x_i+1) − F (x_i)

4. На основании теоремы Бернулли теоретические частоты вычислим по формуле n_i'=np_i

Критерий Пирсона позволяет ответить на вопрос, значимо ли различаются теоретические и эмпирические частоты. В качестве критерия проверки нулевой гипотезы принимается величина

χ2 (2.20)

Можно доказать, что при n→∞ закон распределения случайной величины (2.20) стремится к закону распределения χ2 ,поэтому случайная величина обозначается через χ2 , а сам критерий называют критерием согласия «хи-квадрат».

Число степеней свободы равно ν = k − r −1, где k – число частичных интервалов выборки, r – число оцениваемых параметров. В частности, для нормального распределения оценивают 2 параметра (математическое ожидание и среднее квадратическое отклонение), то есть r = 2. В этом случае ν = k − 3.

Проверим нулевую гипотезу, исходя из требований, что вероятность попадания критерия в правостороннюю критическую область равна принятому уровню значимости α :

χ² > χ_кр² )=α .

Значение критерия, вычисленное по данным наблюдений, обозначим через Χ_набл² и сформулируем правило проверки нулевой гипотезы.

Правило проверки нулевой гипотезы

Для того, чтобы при заданном уровне значимости α проверить гипотезу о соответствии выборочных данных закону F(x), надо вычислить наблюдаемое значение критерия

Затем по таблице критических точек распределения χ2 по заданному уровню значимости α и числу степеней свободы ν = k − r −1 найти критическую точку χ_кр² (α, ν).

Если χ² _наб< χ² _кр , то нет оснований отвергнуть H₀, следовательно, признак Х распределен по закону F(x) .

Если χ² _наб ≥χ² _кр, то H₀ отвергаем и принимаем Н₁, следовательно, признак Х распределен по другому закону.