4.2.3 Решение нелинейных и трансцендентных уравнений

Нелинейные и трансцендентные уравнения можно решать методами касательных, хорд, их комбинацией и др. Эти методы подробно рассматриваются в курсе высшей математики, поэтому здесь их рассмотрение опускается. Напомним только, что по методу касательных

,

а начальное отделение корней выполняется аналитически или графически.

Варианты заданий

1. Определить число членов бесконечного числового ряда, необходимых для вычисления его суммы с заданной точностью , если общий член ряда равен

.

2. Вычислить значение функции c точностью , воспользовавшись ее разложением в ряд

.

Результат проверить с помощью вызова стандартной функции .

3. Для заданного x>1 вычислить по итерационной формуле : с заданной погрешностью , задав начальное приближение . (Сколько итераций пришлось выполнить?) Сравнить с результатом вычислений по встроенной функции.

4. Определить число членов бесконечного числового ряда, необходимых для вычисления его суммы с заданной точностью , если общий член ряда равен

5. Вычислить значение функции с точностью , используя

ее разложение в ряд

Результат проверить с помощью вызова стандартной функции вычисления

синуса.

6. Вычислить с погрешностью значение функции , используя разложение в ряд:

.

Результат проверить с помощью вызова стандартной функции вычисления

косинуса.

7. Определить число членов бесконечного числового ряда, необходимых для вычисления его суммы с точностью , если общий член ряда равен

.

8. Разработать алгоритм и программу для вычисления функции с точностью , воспользовавшись рекуррентной формулой приближенного вычисления значения функции

.

За начальное приближение принять Результат вычислений проверить с помощью формулы

.

9. Вычислить значение функции с точностью , используя ее разложение в ряд

Результат вычислений проверить с помощью вызова стандартной функции вычисления арктангенса.

10. Найдите произведение членов ряда с заданной точностью . Общий член ряда

11. Найдите сумму членов ряда с заданной точностью . Общий член ряда

Сколько итераций пришлось выполнить?

12. Определить число членов бесконечного ряда, необходимых для вычисления его суммы с точностью . Общий член ряда

13. Найти произведение членов ряда с заданной точностью . Общий член ряда

14. Разработать алгоритм и программу для вычисления функции

с заданной погрешностью , воспользовавшись для вычисления рекуррентной формулой

при

15. Определить число членов бесконечного ряда , необходимых для вычисления его суммы с заданной точностью , используя разложение в ряд

.

Результат проверить с помощью вызова стандартной функции вычисления

экспоненты.

16. Разработать алгоритм и программу для вычисления функции с заданной точностью , воспользовавшись рекуррентной формулой

.

За начальное приближение принять Результат проверить с помощью вызова стандартной функции вычисления квадратного корня.

17. Определить число членов бесконечного ряда, необходимых для вычисления его суммы с заданной точностью , используя разложение в ряд

.

18. Определить число членов бесконечного ряда гиперболического синуса , необходимых для вычисления его суммы с заданной точностью , используя разложение в ряд

.

Результат проверить с помощью формулы

.

19. Найдите сумму членов числового ряда с заданной точностью . Общий член ряда

.

20. Для заданных a и p вычислить , используя рекуррентную формулу: .

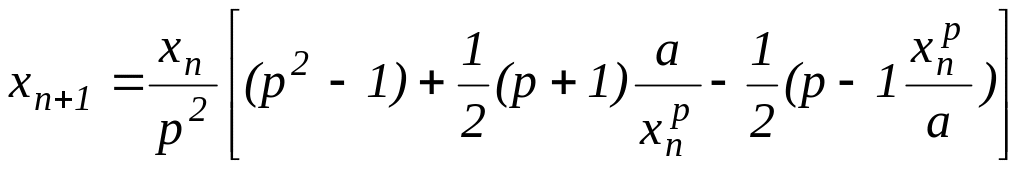Сколько итераций надо выполнить, чтобы для заданной погрешности было справедливо соотношение . При каких начальных приближениях процесс сходится ?

21. Разработать алгоритм и программу для вычисления функции с заданной точностью , используя разложение в ряд

.

Результат проверить с помощью вызова стандартной функции вычисления

экспоненты.

22. Разработать алгоритм и программу для вычисления гиперболического косинуса с заданной точностью , используя разложение в ряд

.

Результат проверить с помощью формулы

.

23. Разработать алгоритм и программу для вычисления функции с заданной точностью , используя разложение в ряд

.

Результат проверить с помощью вызова стандартной функции .

24. Определить число членов бесконечного ряда, необходимых для вычисления его суммы с заданной точностью , используя разложение в ряд

.

25. Найти сумму членов ряда с заданной точностью . Общий член ряда

.

26. Определить число членов бесконечного ряда, необходимых для вычисления его суммы с заданной точностью . Общий член ряда

.

27. Для заданных a и p вычислить , по рекуррентному соотношению

Ньютона:

Сколько итераций надо выполнить, чтобы для заданной погрешности выполнилось соотношение ?

28. Для заданных m и x вычислить бином Ньютона (1+x)^m непосредственно и

по формуле разложения в ряд: .

Для вычисления можно использовать рекуррентное соотношение: либо классическую формулу: . Какой из подходов эффективнее ?

29. Вычислить для заданного значения , используя рекуррентное соотношение:

Сколько итераций надо выполнить для достижения заданной погрешности

, используя условие .

30. Разработать алгоритм и программу решения алгебраического уравнения

методом хорд с точностью до 0,01. При разработке алгоритма следует ввести обозначение .

31. Разработать алгоритм и программу решения трансцендентного уравнения методом касательных с точностью до . При разработке алгоритма следует ввести обозначение

32. Разработать алгоритм и программу решения методом хорд уравнения

на отрезке [1,2;2]с точностью до 0,01.

33. Сравнить методы хорд и касательных поочередно, применяя их, при решении уравнения на отрезке [0.6,1.4]. Точность вычислений задавать поочередно равной 0.1, 0.01,…,0.000001. (Считать количество потребовавшихся приближений.)

34. Сравнить скорость сходимости (число слагаемых для достижения задан-

ной точности ) следующих разложений числа :

,

,

.

35. Сравнить скорость сходимости при вычислении числа e с помощью ряда и бесконечной дроби:

36. Известно равенство . Сколько сомножителей надо взять в произведении, чтобы равенство выполнялось до пятой значащей цифры, то есть с погрешностью не более 10^-5?