6.2 Определение коэффициента сопротивления трения при движении жидкости в трубопроводе

Установка для нахождения коэффициентов гидравлических сопротивлений состоит из напорного бака с водой, трубы с участками разных сечений, двух вентилей и пьезометрических трубок со шкалами. В результате проведенных экспериментов получены данные, которые сведены в таблицу (см. ниже).

Используя данные эксперимента, соответствующие номеру вашего варианта, постоянные экспериментальной установки и расчетные формулы составить блок-схему алгоритма и программу вычисления коэффициента сопротивления трения.

Постоянные экспериментальной установки:

 внутренний диаметр трубопровода d = 0.021 м;

 длина участка = 2.665 м;

 абсолютная шероховатость Δ = 0,0003;

 плотность воды ρ = 1000 кг/м ³

Расчетные формулы

1. Потеря напора на трение

.

2. Средняя скорость жидкости

,

где - плотность воды; m – масса воды, вытекшей из трубопровода за время t; S – площадь сечении трубопровода ( ) .

3. Экспериментальное значение коэффициента Дарси

.

4. Кинематическая вязкость вычисляемая через температуру

.

5. Число Рейнольдса

.

6. Если режим движения жидкости ламинарный (т.е. Re <2320), то

.

7. Если режим движения жидкости турбулентный (Re >2320), то:

7.1) толщина ламинарного подслоя

;

7.2) относительная шероховатость

; 7.3) зона сопротивлений, из сравнения толщины ламинарного подслоя с абсолютной шероховатостью:

а) если >> Δ (т.е. 4Δ) - гидравлически гладкие трубы, коэффициент Дарси определяется по формуле ,

б) если << Δ (т.е. ) - вполне шероховатые трубы, тогда

в) если - не вполне шероховатые трубы; в этом случае коэффициент Дарси определяется через эквивалентную шероховатость Δ_Э

.

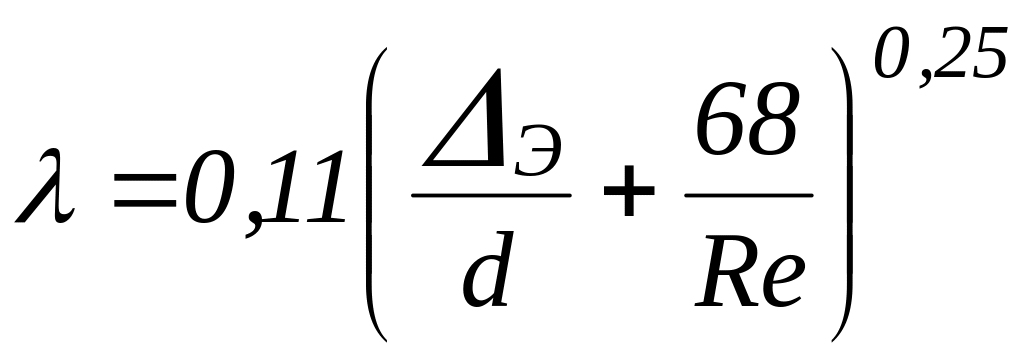Для цельнотянутых стальных водопроводных труб, находящихся в эксплуатации, эквивалентная шероховатость лежит в пределах от до м.

Варианты заданий

№ вари анта	Показания пьезометра А ,м	Показания пьезометра В ,м	Время заполнения мерного бачка t, с	Масса воды в мерном бач ке m, кг	Температура t,
1	1.784	1.782	40	35	15
2	1.780	1.771	40	33	18
3	1.775	1.768	40	30	20
4	1.782	1.774	40	35	16
5	1.772	1.760	40	38	16
6	1.768	1.762	40	30	17
7	1.764	1.761	40	40	15
8	1.770	1.762	40	35	18
9	1.769	1.760	40	38	17
10	1.784	1.774	40	35	16
11	1.780	1.771	40	40	19
12	1.775	1.768	40	33	16
13	1.782	1.774	40	30	18
14	1.772	1.760	40	35	20
15	1.768	1.762	40	38	16
16	1.771	1.761	40	30	16
17	1.770	1.762	40	40	17
18	1.769	1.760	40	35	15
19	1.775	1.770	40	38	18
20	1.782	1.773	40	35	17
21	1.772	1.762	40	40	16
22	1.768	1.760	40	40	19
23	1.772	1.761	40	35	16
24	1.770	1.759	40	38	20
25	1.769	1.760	40	35	15

Список литературы

1. Амелина Н.И. и др. Задачи по программированию. – М. :Вузовская книга, 2000. -102 с.

2. ГОСТ 19.701-90 (ИСО 5807-85). Схемы алгоритмов, программ, данных и систем. – М. Изд-во стандартов, 1991. -26 с.

3. Друзь Б.И., Друзь И.Б., Петрашов С.В. Методические указания к лабораторным работам по гидромеханике и гидравлике. – МГУ им. Г.И. Невельского, 2005. – 19 с.

4. Заводовская А.И., Мендельсон А.А. Построение термодинамических диаграмм. - Владивосток: ДВГМА, 1997. – 15 с.

5. Константинова Е.А. http://webvtsrv/ disc/d.html. Варианты заданий вычисления функций.

6. Культин Н. Delphi 6. Программирование на Object Pascal. – СПб.:БХВ-Петербург, 2003.- 528 с.

7. Пильщиков В Н Сборник упражнений по языку Паскаль. – М.: Наука, Гл. ред. физ.-мат. лит., 1989. – 156 с.

8. Программирование на языке Паскаль. Под ред. О.Ф.Усковой. – СПб.: Питер, 2003.- 332 с.

9. Светозарова Г.И. Мельников А.А. Козловский А.В. Практикум по программированию на языке бейсик. – М. : Наука, Гл. ред. физ.-мат. лит., 1988. – 368 с.

10. Семёнов В.С. Основы алгоритмизации вычислительных процессов: Учеб. пособие. – Владивосток: ДВГМА, 2002. – 21 с.

11. Юркин А.Г. Задачник по программированию. – СПб. : Питер, 2002. – 182 с.

СОДЕРЖАНИЕ

Введение……………………………………………………….……….….... 3

1. Первое приложение………………………………………….…….…...... 4

2. Линейные алгоритмы ……………………………………….………....... 5

Варианты заданий…………………………………………….……….… 6

3. Разветвляющиеся алгоритмы………………………………….……….. 12

3.1 Задачи с простым разветвлением ……………………….……..…. 13

Варианты заданий………………………………………….…….… 14

3.2 Задачи с множественным разветвлением ……………….……….. 18

Варианты заданий………………………………………….………. 20

4. Циклические и итерационные алгоритмы…………………………….. 27

4.1 Некоторые типы задач, приводящие к циклическим алгоритмам 27

Варианты заданий………………………………………….………. 29

4.2 Итерационные алгоритмы………………………………….……… 31

4.2.1 Вычисление суммы ряда простейшим способом …….…….. 31

4.2.2 Вычисление суммы бесконечного ряда с использованием

рекуррентных соотношений………………………….…….. 33

4.2.3 Решение нелинейных и трансцендентных уравнений.……. 35

Варианты заданий…………………………………………..... 35

4.3 Обработка одномерных массивов……………………………….... 40

Варианты заданий……………………………………………..…... 42

4.4 Обработка двумерных массивов………………………………….. 46

Варианты заданий ..………………………………………………... 47

4.5 Сортировка массивов…………………….…………...….……….. 54

Варианты заданий………………………………………….……..... 56

5. Рекурсия…………………………………………………………………..57

5.1 Вычисление факториала числа ……………………………………..58

Варианты заданий……………………………….………………..... ..58

6. Примеры профессиональных задач……………………………………..60

6.1 Вычисление объемов и давлений газа в идеальном цикле со

смешанным подводом теплоты…………………………………….60

Варианты заданий………………………………………….……......64

6.2 Определение коэффициента сопротивления трения при

движении жидкости в трубопроводе………………………………65

Варианты заданий……………………………….………….…….....67

7. Список литературы………………………………………………..……..68

Позиция №

в плане издания

учебной литературы

Виталий Сергеевич Семенов

Сборник задач и упражнений по алгоритмизации и программированию

Печатается в авторской редакции с готового оригинал-макета

4 уч.-изд. л. Формат 60*84 1/16

Т ираж 100 экз. Заказ 18

Отпечатано в типографии ИПК МГУ им. адм. Г.И. Невельского

Владивосток, 59, ул. Верхнепортовая, 50а