3. Построение и оценка моделей, выбор наиболее адекватной из них.
Для начала построим линейную модель, включив в нее все имеющиеся у нас переменные:
Dependent Variable: CRIME_RATE |
||||
Method: Least Squares |
||||
Date: 05/04/08 Time: 22:11 |
||||
Sample(adjusted): 1 185 |
||||
Included observations: 185 after adjusting endpoints |
||||
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
39.21527 |
37.90886 |
1.034462 |
0.3024 |
POPULATION |
8.89E-07 |
2.15E-06 |
0.412381 |
0.6806 |
BELOW_POVERTY |
-0.229843 |
0.465316 |
-0.493951 |
0.6220 |
COLOR_POPULATION |
0.340434 |
0.128709 |
2.644983 |
0.0089 |
HIGH_SCHOOL |
0.491847 |
0.425204 |
1.156731 |
0.2490 |
HOUSEHOLD_INCOME |
-0.000891 |
0.000266 |
-3.345320 |
0.0010 |
POP__DENSITY |
-0.001948 |
0.000572 |
-3.407178 |
0.0008 |
COAST |
-3.152259 |
3.158178 |
-0.998126 |
0.3196 |
LAKE |
-4.255409 |
4.266458 |
-0.997410 |
0.3200 |
UNEMPLOYMENT |
1.952430 |
0.877059 |
2.226109 |
0.0273 |
BACHELOR |
-0.118809 |
0.216929 |
-0.547687 |
0.5846 |
OFFICERS_PER _1000 |
4.774611 |
2.132493 |
2.238981 |
0.0264 |
R-squared |
0.444933 |
Mean dependent var |
57.93291 |
|
Adjusted R-squared |
0.409640 |
S.D. dependent var |
21.94113 |
|
S.E. of regression |
16.85844 |
Akaike info criterion |
8.550245 |
|
Sum squared resid |
49167.81 |
Schwarz criterion |
8.759133 |
|
Log likelihood |
-778.8977 |
F-statistic |
12.60675 |
|
Durbin-Watson stat |
2.148014 |
Prob(F-statistic) |
0.000000 |
|
Прежде всего представляется необходимым проверить гипотезы о значимости каждого коэффициента в отдельности и о значимости полученного уравнения регрессии в целом. Проверка первого вида гипотез осуществляется на основе t-статистики.
Как видно из модели, всего 5 переменные оказались значимыми. Три из них на 1% уровне значимости (tкрит.=2,576), два фактора на 5 % уровне (tкрит.=1,96).
Проверка гипотезы о значимости уравнения регрессии в целом говорит о том, что уравнение в целом также значимо F-стат> F-крит. = 2,32 на 1% уровне значимости.
Можно попробовать улучшить модель, например, объединить какие-нибудь переменные в одну. С этой целью был проведен тест Вальда для различных комбинаций переменных. В результате получаем, что наши фиктивные переменные можно объединить в одну с вероятностью около 80%:
Wald Test: |
||||
Equation: LYNEYNAYA |
||||
Null Hypothesis: |
C(8)=C(9) |
|||
F-statistic |
0.066198 |
|
Probability |
0.797260 |
Chi-square |
0.066198 |
|
Probability |
0.796955 |
После объединения переменных получим новую модель:
Dependent Variable: CRIME_RATE |
||||
Method: Least Squares |
||||
Date: 05/04/08 Time: 22:23 |
||||
Sample(adjusted): 1 185 |
||||
Included observations: 185 after adjusting endpoints |
||||
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
40.96040 |
37.19693 |
1.101177 |
0.2723 |
POPULATION |
7.88E-07 |
2.11E-06 |
0.372702 |
0.7098 |
BELOW_POVERTY |
-0.254230 |
0.454336 |
-0.559564 |
0.5765 |
COLOR_POPULATION |
0.348694 |
0.124306 |
2.805133 |
0.0056 |
HIGH_SCHOOL |
0.476794 |
0.420028 |
1.135147 |
0.2579 |
HOUSEHOLD_INCOME |
-0.000898 |
0.000264 |
-3.399391 |
0.0008 |
POP__DENSITY |
-0.001958 |
0.000569 |
-3.441118 |
0.0007 |
COAST+LAKE |
-3.456942 |
2.919890 |
-1.183929 |
0.2381 |
UNEMPLOYMENT |
1.901410 |
0.852053 |
2.231563 |
0.0269 |
BACHELOR |
-0.106068 |
0.210633 |
-0.503566 |
0.6152 |
OFFICERS_PER_100 |
4.688190 |
2.100216 |
2.232242 |
0.0269 |
R-squared |
0.444721 |
Mean dependent var |
57.93291 |
|
Adjusted R-squared |
0.412808 |
S.D. dependent var |
21.94113 |
|
S.E. of regression |
16.81314 |
Akaike info criterion |
8.539817 |
|
Sum squared resid |
49186.63 |
Schwarz criterion |
8.731298 |
|
Log likelihood |
-778.9331 |
F-statistic |
13.93560 |
|
Durbin-Watson stat |
2.145300 |
Prob(F-statistic) |
0.000000 |
|
Модель в целом улучшилась, но как вы можете видеть, не сильно. Мы получаем все те же 4 значимых на 1 % уровне переменных, чуть более высокое значение F-статистики.
Встает вопрос о причинах незначимости большей части факторов, что наталкивает нас на размышления, что в модели присутствует мультиколлинеарность между регрессорами.
Существует 4 признака мультиколлинеарности:
При малом изменении исходных данных сильно изменяются оценки;
Знаки и значения коэффициентов отличаются от ожидаемых;
Существует сильная корреляция между признаками;
Некоторые параметры незначимы по отдельности, но все уравнение в целом значимо.
В нашем случае, как отмечалось выше, многие параметры оказались незначимыми, но в целом уравнение значимо. Кроме того, можно предположить наличие взаимосвязи между некоторыми регрессорами. Чтобы проверить данное предположение обратимся к корелляционной матрице:
|
CRIME_ RATE |
BACHELOR |
BELOW_ POVERTY |
COLOR_ POPULATION |
HIGH_ SCHOOL |
HOUSEHOLD_INCOME |
OFFICERS_ PER_100 |
POP__ DENSITY |
POPULATION |
COAST |
LAKE |
UNEMPLOYMENT |
CRIME_RATE |
1.000000 |
-0.277569 |
0.489003 |
0.362530 |
-0.318363 |
-0.555917 |
0.363355 |
-0.113640 |
-0.030831 |
-0.019600 |
0.060799 |
0.368475 |
BACHELOR |
-0.277569 |
1.000000 |
-0.339629 |
-0.372007 |
0.679217 |
0.450594 |
-0.207448 |
-0.154472 |
-0.019632 |
-0.005918 |
-0.219186 |
-0.455858 |
BELOW_POVERTY |
0.489003 |
-0.339629 |
1.000000 |
0.599881 |
-0.631420 |
-0.843784 |
0.545597 |
0.243514 |
0.110962 |
0.115226 |
0.265791 |
0.510779 |
COLOR_POPULATION |
0.362530 |
-0.372007 |
0.599881 |
1.000000 |
-0.816645 |
-0.396327 |
0.615731 |
0.475663 |
0.310647 |
0.332219 |
0.039895 |
0.447369 |
HIGH_SCHOOL |
-0.318363 |
0.679217 |
-0.631420 |
-0.816645 |
1.000000 |
0.534761 |
-0.537921 |
-0.515884 |
-0.250445 |
-0.286587 |
-0.152017 |
-0.505132 |
HOUSEHOLD_INCOME |
-0.555917 |
0.450594 |
-0.843784 |
-0.396327 |
0.534761 |
1.000000 |
-0.462152 |
-0.061379 |
-0.008048 |
-0.009355 |
-0.200710 |
-0.410054 |
OFFICERS_PER_100 |
0.363355 |
-0.207448 |
0.545597 |
0.615731 |
-0.537921 |
-0.462152 |
1.000000 |
0.475774 |
0.303678 |
0.189547 |
0.265858 |
0.374468 |
POP__DENSITY |
-0.113640 |
-0.154472 |
0.243514 |
0.475663 |
-0.515884 |
-0.061379 |
0.475774 |
1.000000 |
0.556692 |
0.241272 |
0.233570 |
0.209880 |
POPULATION |
-0.030831 |
-0.019632 |
0.110962 |
0.310647 |
-0.250445 |
-0.008048 |
0.303678 |
0.556692 |
1.000000 |
-0.002908 |
0.175121 |
0.057214 |
COAST |
-0.019600 |
-0.005918 |
0.115226 |
0.332219 |
-0.286587 |
-0.009355 |
0.189547 |
0.241272 |
-0.002908 |
1.000000 |
-0.328639 |
0.049080 |
LAKE |
0.060799 |
-0.219186 |
0.265791 |
0.039895 |
-0.152017 |
-0.200710 |
0.265858 |
0.233570 |
0.175121 |
-0.328639 |
1.000000 |
0.366052 |
UNEMPLOYMENT |
0.368475 |
-0.455858 |
0.510779 |
0.447369 |
-0.505132 |
-0.410054 |
0.374468 |
0.209880 |
0.057214 |
0.049080 |
0.366052 |
1.000000 |
Данные таблицы свидетельствуют о наличии мультиколлинеарности между HOUSEHOLD_INCOME и BELOW_POVERTY; HIGH_SCHOOL и COLOR_POPULATION; COLOR_POPULATION и BELOW_POVERTY; HIGH_SCHOOL и BACHELOR . В этой связи нам придется исключить из модели BELOW_POVERTY и HIGH_SCHOOL, так как они меньше всего кореллируют с зависимой переменной. Исключение этих переменных имеет содержательную интерпретацию: вполне логично, что фактор доходов домашних хозяйств будет тесно связан с долей людей, живущих за чертой бедности; так и оба фактора, определяющие «образованность» населения оказались тесно связанными.
После исключения данных переменных из модели, получаем новую модель:
Dependent Variable: CRIME_RATE |
||||
Method: Least Squares |
||||
Sample(adjusted): 1 185 |
||||
Included observations: 185 after adjusting endpoints |
||||
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
70.37594 |
9.711678 |
7.246528 |
0.0000 |
COLOR_POPULATION |
0.225504 |
0.082162 |
2.744628 |
0.0067 |
BACHELOR |
0.012626 |
0.149067 |
0.084698 |
0.9326 |
HOUSEHOLD_INCOME |
-0.000718 |
0.000149 |
-4.805760 |
0.0000 |
POP__DENSITY |
-0.002248 |
0.000521 |
-4.311285 |
0.0000 |
COAST+LAKE |
-4.100658 |
2.869932 |
-1.428835 |
0.1548 |
UNEMPLOYMENT |
1.813072 |
0.820489 |
2.209747 |
0.0284 |
OFFICERS_PER_100 |
5.032656 |
2.082302 |
2.416871 |
0.0167 |
POPULATION |
1.04E-06 |
2.10E-06 |
0.494553 |
0.6215 |
R-squared |
0.439093 |
Mean dependent var |
57.93291 |
|
Adjusted R-squared |
0.413597 |
S.D. dependent var |
21.94113 |
|
S.E. of regression |
16.80185 |
Akaike info criterion |
8.528280 |
|
Sum squared resid |
49685.16 |
Schwarz criterion |
8.684946 |
|
Log likelihood |
-779.8659 |
F-statistic |
17.22218 |
|
Durbin-Watson stat |
1.892986 |
Prob(F-statistic) |
0.000000 |
|
Как мы видим, данная модель содержит большее количество значимых переменных Теперь к списку значимых регрессоров добавляется константа.
Все же большое количество переменных
в модели остается незначимым, также
значения F-статистики и
остаются сравнительно невысокими. В
этой связи приступим к поиску наилучшей
модели и с этой целью рассмотрим
полулогарифмическую и логарифмическую
модели. При этом для улучшения модели
переменная population была
исключена из списка регрессоров, так
как достаточно сильно кореллирует с
pop_density и
очень слабо с зависимой переменной.
Результаты моделирования представлены
ниже.
Полулогарифмическая модель:
Dependent Variable: LOG(CRIME_RATE) |
||||
Method: Least Squares |
||||
Sample(adjusted): 1 185 |
||||
Included observations: 185 after adjusting endpoints |
||||
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
4.305461 |
0.165641 |
25.99277 |
0.0000 |
COLOR_POPULATION |
0.004217 |
0.001400 |
3.011841 |
0.0030 |
BACHELOR |
0.000546 |
0.002547 |
0.214185 |
0.8306 |
HOUSEHOLD_INCOME |
-1.51E-05 |
2.56E-06 |
-5.894379 |
0.0000 |
POP__DENSITY |
-3.86E-05 |
7.89E-06 |
-4.885155 |
0.0000 |
COAST+LAKE |
-0.063280 |
0.048706 |
-1.299229 |
0.1956 |
UNEMPLOYMENT |
0.029563 |
0.014026 |
2.107765 |
0.0365 |
OFFICERS_PER_100 |
0.084965 |
0.035575 |
2.388363 |
0.0180 |
R-squared |
0.489252 |
Mean dependent var |
3.985172 |
|
Adjusted R-squared |
0.469053 |
S.D. dependent var |
0.394689 |
|
S.E. of regression |
0.287594 |
Akaike info criterion |
0.387747 |
|
Sum squared resid |
14.63973 |
Schwarz criterion |
0.527006 |
|
Log likelihood |
-27.86660 |
F-statistic |
24.22155 |
|
Durbin-Watson stat |
1.966414 |
Prob(F-statistic) |
0.000000 |
|
В данной модели 6 значимых регрессоров, также увеличилось значение F- статистики и . Хоть увеличение данного значения и не говорит об улучшении модели, так как в представленных моделях включен разный список регрессоров, но говорит о том, что большая доля дисперсии результирующей переменной может быть объяснено при помощи данного уравнения регрессии.
Логарифмическая модель:
Dependent Variable: LOG(CRIME_RATE) |
||||
Method: Least Squares |
||||
Sample(adjusted): 1 185 |
||||
Included observations: 184 |
||||
Excluded observations: 1 after adjusting endpoints |
||||
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
12.51503 |
1.209308 |
10.34892 |
0.0000 |
LOG(COLOR_POPULATION) |
0.137704 |
0.046669 |
2.950648 |
0.0036 |
LOG(BACHELOR) |
0.035008 |
0.071182 |
0.491809 |
0.6235 |
LOG(HOUSEHOLD_INCOME) |
-0.866089 |
0.114534 |
-7.561839 |
0.0000 |
LOG(POP__DENSITY) |
-0.119242 |
0.035642 |
-3.345577 |
0.0010 |
COAST+LAKE |
-0.064809 |
0.050591 |
-1.281032 |
0.2019 |
LOG(UNEMPLOYMENT) |
0.097145 |
0.082600 |
1.176088 |
0.2412 |
LOG(OFFICERS_PER_100) |
-0.024178 |
0.065659 |
-0.368226 |
0.7131 |
LOG(POPULATION) |
0.077332 |
0.030065 |
2.572177 |
0.0109 |
R-squared |
0.504407 |
Mean dependent var |
3.987750 |
|
Adjusted R-squared |
0.481751 |
S.D. dependent var |
0.394200 |
|
S.E. of regression |
0.283783 |
Akaike info criterion |
0.366462 |
|
Sum squared resid |
14.09324 |
Schwarz criterion |
0.523715 |
|
Log likelihood |
-24.71454 |
Durbin-Watson stat |
1.922565 |
|
Данная модель содержит только 5 значимых регрессоров. Остальные показатели также дают возможности предполагать, что логарифмическая модель лучше какой-либо из ранее рассмотренных .
Исследовав различные варианты моделей, мы сделали некоторые выводы.
Как вы можете видеть ни в одной из исследуемых моделей фиктивная переменная не стала значимой, следовательно, скорее всего, нужно исключить ее из модели и сделать вывод, что предположение о качественных различиях уровня преступности по городам нет. В этой связи мы предлагаем ввести новую фиктивную переменную, которая принимает значение 1, если исследуется «известный город» (например, Нью-Йорк) и 0, если «неизвестный» (авторы проекта понимают, что знания людей сильно различаются, так некоторые города являются «известными» для одних и «неизвестными» для других людей, в этой связи «известными» городами выбраны в основном крупные города, сведения о которых часто встречаются в средствах массовой информации).
Так как во всех ранее рассмотренных моделях ни разу коэффициент перед переменной bachelor и officers_per_100 не становился значимым, следовательно, стоит рассмотреть некие другие функциональные связи между зависимой переменной и данными переменными.
С этой посмотрим еще раз на парные корелляционные поля зависимости:
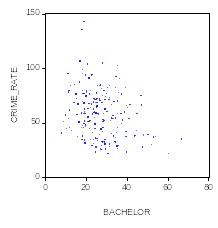
Как нам показалось, данная связь напоминает некую обратную (гиперболическую) зависимость, то есть crime_rate=f(1/bachelor).
Аналогичным образом рассмотрим зависимость crime_rate от officers_per_100:
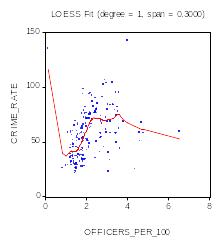
Аналогично предыдущему случаю можно сделать предположение об обратной зависимости зависимой переменной от данного фактора crime_rate=f(1/officers_per_100).
Также после многочисленных попыток построить модель с фиктивными переменными, была получена переменная fiction, принимающая значений 1, если город находится в Северо-Западных штатах США (Пенсильвания, Нью-Йорк, Нью-Джерси и т.д.), наиболее развитых «приозерных» штатах (Мичиган, Висконсин) или в Калифорнии, и принимающая значение 0 в противном случае.
С учетом данных корректировок и введения новой фиктивной переменной (fiction), авторы проекта рассмотрели различные виды моделей. Были рассмотрены линейная, логарифмическая, полулогарифмическая модели, различные вариации смесей данных моделей3. В конце концов, была найдена наилучшая модель:
Dependent Variable: CRIME_RATE |
||||
Method: Least Squares |
||||
Sample(adjusted): 1 185 |
||||
Included observations: 185 after adjusting endpoints |
||||
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
84.02060 |
8.107515 |
10.36330 |
0.0000 |
COLOR_POPULATION |
0.327883 |
0.073136 |
4.483228 |
0.0000 |
1/(BACHELOR) |
-177.7898 |
84.73426 |
-2.098205 |
0.0373 |
HOUSEHOLD_INCOME |
-0.000945 |
0.000131 |
-7.228020 |
0.0000 |
UNEMPLOYMENT |
2.408578 |
0.805781 |
2.989121 |
0.0032 |
1/(OFFICERS_PER_100) |
8.279515 |
1.874372 |
4.417221 |
0.0000 |
POP__DENSITY |
-0.001818 |
0.000407 |
-4.469260 |
0.0000 |
R-squared |
0.478084 |
Mean dependent var |
57.93291 |
|
Adjusted R-squared |
0.460491 |
S.D. dependent var |
21.94113 |
|
S.E. of regression |
16.11603 |
Akaike info criterion |
8.434610 |
|
Sum squared resid |
46231.32 |
Schwarz criterion |
8.556461 |
|
Log likelihood |
-773.2014 |
Durbin-Watson stat |
1.683856 |
|
Все регрессоры модели оказались значимы на 5% уровне. Уравнение в целом также значимо. Коэффициент остался по-прежнему невысоким. Строго говоря, данное значение является не высоким, что говорит о том, что значительная часть разброса данных моделью не объяснена. В этой связи нужно сказать, что сравнительно невысокое значение указывает не на то, что модель оказалась неудачной и подобрана плохая функциональная зависимость, а на то, что в модель должны быть включены дополнительные регрессоры, такие как условия жизни человека, его психическое состояние и др (так как именно психологические причины в основном определяют склонность к преступлению людей). Но темой нашего проекта являются именно влияния различных экономических, демографических и социально-политических показателей на уровень преступности, и ,как вы можете понять, исследовать психологические факторы не является возможным.
Проверка на устойчивость
Для проверки на гетероскедастичность нашей новой модели воспользуемся самым универсальным тестом - тестом Уайта. Рассмотрим две формы теста Уайта: с учетом перекрестных эффектов и без.
а) Тест Уайта(cross terms):
White Heteroskedasticity Test: |
|||
F-statistic |
0.586153 |
Probability |
0.947971 |
Obs*R-squared |
16.94093 |
Probability |
0.932569 |
Данный тест говорит, что гипотеза о гомоскедастичности принимается с вероятностью почти 95%
б) Тест Уайта (no cross terms)
White Heteroskedasticity Test: |
|||
F-statistic |
0.593878 |
Probability |
0.845231 |
Obs*R-squared |
7.360213 |
Probability |
0.832920 |
Данный тест также отвергает гипотезу о наличии гетероскедастичности с вероятностью 85%.
По результатам теста Уайта можно судить об отсутствии гетероскедастичности.
Рассмотрим другие тесты на обнаружение гетероскедастичности:
Тест Глейзера
Посмотрев графики зависимости остатков регрессии от всех переменных, мы пришли к выводу, что дисперсия ошибки, скорее всего, зависит от переменной unemployment.
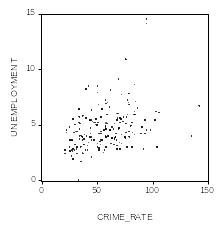
В этой связи можно сделать предположение, что дисперсия остатков регрессии функционально зависит от данной переменной. Проводя регрессию
ln(
)
=
,
получаем следующие значения:
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
2.595810 |
0.207409 |
12.51542 |
0.0000 |
UNEMPLOYMENT |
-0.119724 |
0.041209 |
-2.905300 |
0.0041 |
и функциональную зависимость дисперсии остатков от безработицы
ln(ost)=
,
Коэффициенты оказались значимы на уровне значимости 1%, поэтому мы не принимаем нулевую гипотезу о наличии гомоскедастичности.
Также были сделаны попытки подобрать такую функциональную зависимость для других переменных, но все коэффициенты получались незначимыми.
Тест Голдфельдта-Квандта: основная гипотеза не меняется, альтернативная утверждает, что дисперсия ошибки пропорциональна одному из регрессоров ( ~unemployment). Упорядочиваем все наблюдения нашей выборки по величине unemployment, после чего оцениваем отдельно регрессии для первых 70 наблюдений:
Dependent Variable: CRIME_RATE |
||||
Method: Least Squares |
||||
Date: 05/06/08 Time: 21:25 |
||||
Sample(adjusted): 3 74 IF UNEMPLOYMENT<4 |
||||
Included observations: 70 after adjusting endpoints |
||||
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
78.12301 |
15.26960 |
5.116245 |
0.0000 |
COLOR_POPULATION |
0.188853 |
0.123665 |
1.527131 |
0.1316 |
1/(BACHELOR) |
-145.7342 |
136.2772 |
-1.069395 |
0.2888 |
HOUSEHOLD_INCOME |
-0.000441 |
0.000158 |
-2.789841 |
0.0069 |
UNEMPLOYMENT |
5.285210 |
2.488191 |
2.124118 |
0.0375 |
1/(OFFICERS_PER_100) |
-47.06642 |
13.21287 |
-3.562164 |
0.0007 |
POP__DENSITY |
0.001113 |
0.001095 |
1.016766 |
0.3130 |
R-squared |
0.541360 |
Mean dependent var |
49.52322 |
|
Adjusted R-squared |
0.499024 |
S.D. dependent var |
18.87582 |
|
S.E. of regression |
13.36024 |
Akaike info criterion |
8.114609 |
|
Sum squared resid |
11602.24 |
Schwarz criterion |
8.335951 |
|
Log likelihood |
-285.1259 |
Durbin-Watson stat |
1.938454 |
|
Проведем ту же операцию для последних 70 наблюдений:
Dependent Variable: CRIME_RATE |
||||
Method: Least Squares |
||||
Date: 05/06/08 Time: 21:27 |
||||
Sample(adjusted): 116 187 IF UNEMPLOYMENT>4.8 |
||||
Included observations: 70 after adjusting endpoints |
||||
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
112.9164 |
14.98243 |
7.536590 |
0.0000 |
COLOR_POPULATION |
0.233528 |
0.123516 |
1.890662 |
0.0631 |
1/(BACHELOR) |
-102.9340 |
134.5980 |
-0.764751 |
0.4472 |
HOUSEHOLD_INCOME |
-0.001019 |
0.000319 |
-3.192302 |
0.0022 |
UNEMPLOYMENT |
1.163254 |
1.323696 |
0.878792 |
0.3828 |
1/(OFFICERS_PER_100) |
-24.52977 |
17.29577 |
-1.418253 |
0.1609 |
POP__DENSITY |
-0.002624 |
0.000742 |
-3.537910 |
0.0008 |
R-squared |
0.460543 |
Mean dependent var |
65.11735 |
|
Adjusted R-squared |
0.410747 |
S.D. dependent var |
20.87254 |
|
S.E. of regression |
16.02234 |
Akaike info criterion |
8.478011 |
|
Sum squared resid |
16686.51 |
Schwarz criterion |
8.699354 |
|
Log likelihood |
-298.2084 |
Durbin-Watson stat |
1.826011 |
|
Получаем следующие значения ESS1=11602.24и ESS2=16686.51. Получаем значение F-статистики F=ESS2/ESS1=1,44. Критическое значении статистики Фишера F=1,53, следовательно, гипотеза о наличии гетероскедастичности не принимается на 5% уровне значимости.
Тест Бреуша-Пагана:
Основная гипотеза
по-прежнему утверждает о присутствии
гомоскедастичности в модели H1:
=
Шаги:
1) OLS ei
2) σ2оцен.=
3)
=
+
OLS
ESS
4)
~
χ2(p)
если Ho верна, статистика
имеет распределение хи квадрат Пирсона.
Сумма
квадратов остатков нашей модели
=
46231.32,
следовательно, σ2оцен.=249,9
Далее оценим регрессию = +
Dependent Variable: BPAGAN |
||||
Method: Least Squares |
||||
Date: 05/06/08 Time: 21:41 |
||||
Sample(adjusted): 3 185 |
||||
Included observations: 183 after adjusting endpoints |
||||
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
1.087185 |
0.452764 |
2.401218 |
0.0174 |
UNEMPLOYMENT |
-0.016707 |
0.093649 |
-0.178398 |
0.8586 |
R-squared |
0.000176 |
Mean dependent var |
1.010885 |
|
Adjusted R-squared |
-0.005348 |
S.D. dependent var |
2.004562 |
|
S.E. of regression |
2.009915 |
Akaike info criterion |
4.244931 |
|
Sum squared resid |
731.1964 |
Schwarz criterion |
4.280007 |
|
Log likelihood |
-386.4112 |
F-statistic |
0.031826 |
|
Durbin-Watson stat |
2.129984 |
Prob(F-statistic) |
0.858610 |
|
Далее
рассмотрим статистику
=
0,016, распределенную по закону
,
95%-критическое значение которой равно
3,84. Таким образом, гипотеза о
гомоскедастичности подтверждается.
Коррекция Гетероскедастичности:
В результате проведенных тестов мы
получили, что в модели есть подозрение
на гетероскедастичность по переменной
unemployment . Для ее устранения
проведем коррекцию с помощью взвешенного
метода наименьших квадратов, где в
качестве весов, основываясь на выявленной
тестами Глейзера зависимости дисперсии
остаточного члена регрессии от
безработицы, возьмем величину ves2=(
.В
итоге получаем взвешенную МНК:
Dependent Variable: CRIME_RATE |
||||
Method: Least Squares |
||||
Date: 05/06/08 Time: 21:50 |
||||
Sample(adjusted): 3 187 |
||||
Included observations: 185 after adjusting endpoints |
||||
Weighting series: 1/VES2^2 |
||||
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
89.35560 |
7.666220 |
11.65576 |
0.0000 |
COLOR_POPULATION |
0.335664 |
0.068823 |
4.877227 |
0.0000 |
1/(BACHELOR) |
-157.6997 |
75.94108 |
-2.076606 |
0.0393 |
HOUSEHOLD_INCOME |
-0.001037 |
0.000138 |
-7.514900 |
0.0000 |
UNEMPLOYMENT |
1.935921 |
0.463821 |
4.173856 |
0.0000 |
1/(OFFICERS_PER_100) |
8.151802 |
2.070356 |
3.937392 |
0.0001 |
POP__DENSITY |
-0.001917 |
0.000389 |
-4.924945 |
0.0000 |
Weighted Statistics |
|
|
|
|
R-squared |
0.911019 |
Mean dependent var |
60.84145 |
|
Adjusted R-squared |
0.908020 |
S.D. dependent var |
51.36984 |
|
S.E. of regression |
15.57958 |
Akaike info criterion |
8.366903 |
|
Sum squared resid |
43204.75 |
Schwarz criterion |
8.488754 |
|
Log likelihood |
-766.9385 |
Durbin-Watson stat |
1.827524 |
|
Unweighted Statistics |
|
|
|
|
R-squared |
0.475418 |
Mean dependent var |
57.93291 |
|
Adjusted R-squared |
0.457736 |
S.D. dependent var |
21.94113 |
|
S.E. of regression |
16.15714 |
Sum squared resid |
46467.47 |
|
Durbin-Watson stat |
1.823530 |
|
|
|
Как вы можете видеть, все коэффициенты значимы на 5% уровне. Значение F-статистики=
, следоватедьно, уравнение в целом также. Также увеличилось значение и достигло 0,91 (91% дисперсии результирующей переменной может быть объяснен при помощи данного уравнения регрессии).
Проверим, сохранилась ли в модели гетероскедастичность по переменной unemployment.
С этой целью снова рассмотрим тест Уайта и Глейзера (проводить еще раз тесты Голфелда-Квандта и Бреуша-Пагана мы считаем нецелесообразным, так как они отклонили гипотезу о наличии гетероскедастичности по данной переменной).
Тест Уайта.
а) cross terms:
White Heteroskedasticity Test: |
|||
F-statistic |
0.492063 |
Probability |
0.983600 |
Obs*R-squared |
14.43370 |
Probability |
0.976649 |
б) no cross terms:
White Heteroskedasticity Test: |
|||
F-statistic |
0.595372 |
Probability |
0.844014 |
Obs*R-squared |
7.377988 |
Probability |
0.831658 |
Тест Уайта еще более уверенно отвергает гипотезу о наличии гетероскедастичности.
Тест Глейзера.
Аналогично предыдущему случаю рассмотрим регрессию абсолютных значений остатков нашей новой (взвешенной) модели от unemployment. Получаем:
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
2.292632 |
0.130360 |
17.58694 |
0.0000 |
UNEMPLOYMENT |
-0.168354 |
0.091066 |
-1.848707 |
0.0661 |
Коэффициент при unemployment оказался незначимым, следовательно, гипотеза о гетероскедастичности отвергается.
Из данных тестов можно сделать вывод, что гетероскедастичность в модели устранена.