
- •Защищена___________ Оценка______________
- •Введение
- •1 Гидравлический расчёт разветвлённого трубопровода
- •1.1 Подбор труб
- •1.2 Расчёт потерь на трение в основной магистрали
- •1.3 Расчёт ответвлений
- •1.4 Построение пьезометрического графика
- •1.5 Расчет всасывающей магистрали
- •1.5.1 Определение потерь в колене
- •1.5.2 Определяем потери напора в фильтре
- •1.6 Выбор насоса
- •2 Гидродинамический расчёт короткого трубопровода
- •2.1 Расчёт первого участка – резкое сужение
- •2.2 Расчёт второго участка – диффузор
- •2.3 Расчёт третьего участка – задвижка
- •3.2 Расчёт параметров газа во входном сечении
- •3.3 Расчёт параметров газа в выходном сечении
- •3.4 Геометрический профиль сопла
- •3.4.1 Обобщение результатов
- •3.5 Расчёт дополнительных сечений
2.1 Расчёт первого участка – резкое сужение
Определяем скорость W, на первом участке:
![]() ; (2.1)
; (2.1)
где
![]() ,
,
![]() - плотность жидкости;
- плотность жидкости;
![]() ;
;
![]()
Число Рейнольдса Re на первом участке определяется по формуле:
![]() ; (2.2)
; (2.2)
где
![]() ,
,
![]() -
вязкость жидкости;
-
вязкость жидкости;
![]()
![]()
Абсолютную
шероховатость
![]() ,
м для цельносварных стальных труб
определяется из / ист. 1 приложение 2/. Мы
взяли этот коэффициент для новых или
старых в лучшем состоянии, сварные или
клепанные соединения.
,
м для цельносварных стальных труб
определяется из / ист. 1 приложение 2/. Мы
взяли этот коэффициент для новых или
старых в лучшем состоянии, сварные или
клепанные соединения.
![]() ;
;
Находим
относительную
![]() ,
м шероховатость на первом участке:
,
м шероховатость на первом участке:
![]() ;
;
Определяем режим течения на первом участке:
![]() ;
;
Сравним
![]() с числом Рейнольдса
с числом Рейнольдса
![]() .
.
При
сравнении получили область гладкостенного
режима, т.е.
![]() .
Коэффициент
.
Коэффициент
![]() рассчитывается по формуле Блазиуса:
рассчитывается по формуле Блазиуса:
![]() ; (2.3)
; (2.3)
![]() .
.
Определяем потери h, м по длине трубопровода:
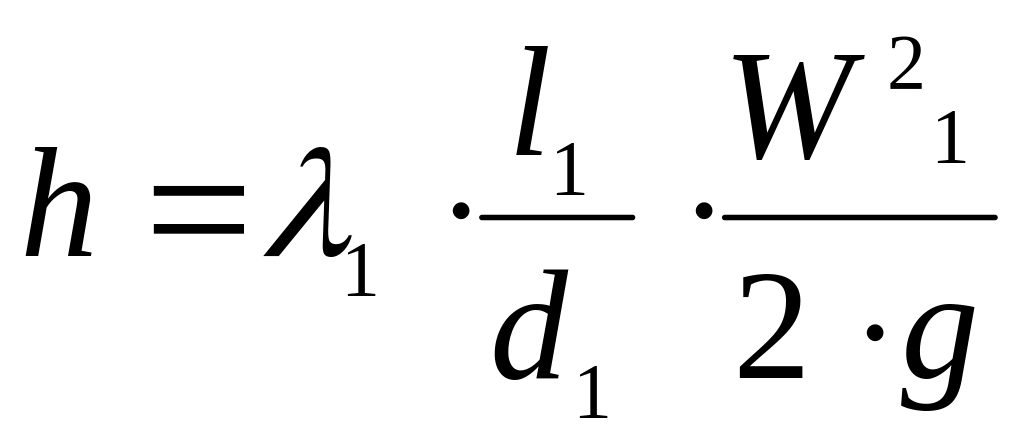 ; (2.4)
; (2.4)
![]() .
.
Вычислим
потери на резком сужении
![]() ,
м на первом участке:
,
м на первом участке:
![]() ; (2.5)
; (2.5)
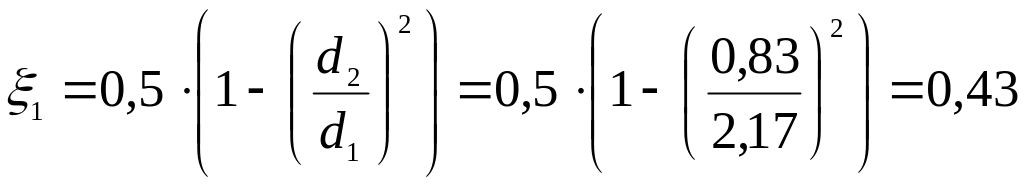 ;
;
![]() .
.
2.2 Расчёт второго участка – диффузор
Определяем скорость W, на втором участке из формулы (2.1):
![]() ;
;
где , - плотность жидкости;
![]() ;
;
![]() .
.
Число Рейнольдса Re на втором участке определяется по формуле (2.2):
![]() ;
;
где , - вязкость жидкости;
;
![]() .
.
Абсолютная шероховатость , м для цельносварных стальных труб определяется из / ист. 1 приложение 2/ :
;
Находим
относительную шероховатость
![]() ,
м; на втором участке:
,
м; на втором участке:
![]() ;
;
Определяем режим течения на втором участке:
![]() ;
;
Сравним
![]() с числом Рейнольдса
с числом Рейнольдса
![]() .
.
При сравнении получили область гладкостенного режима, т.е. . Коэффициент рассчитывается по формуле Блазиуса (2.3):
;
![]() .
.
Определяем потери по h, м длине трубопровода по формуле (2.4):
![]() .
.
Вычислим
потери
![]() ,
м на местных сопротивлениях на втором
участке по формуле (2.5):
,
м на местных сопротивлениях на втором
участке по формуле (2.5):
![]() ;
;
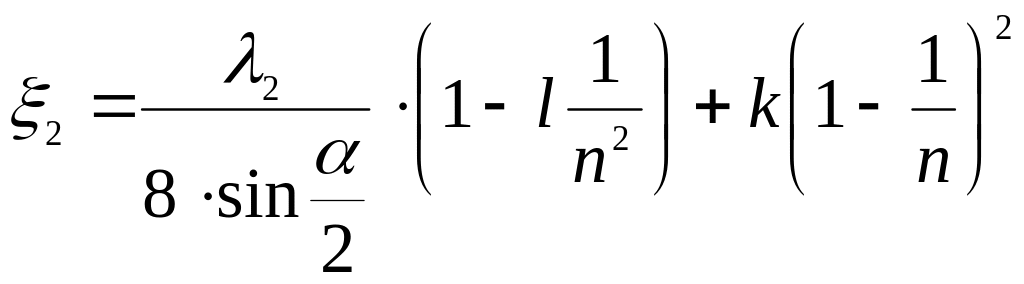 ;
;
Где
![]() ;
;
![]() ;
;
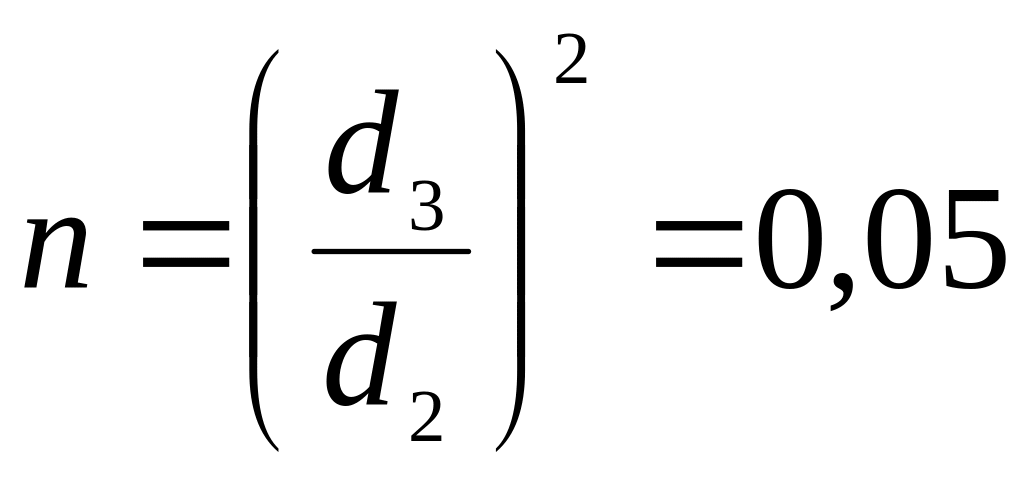 .
.
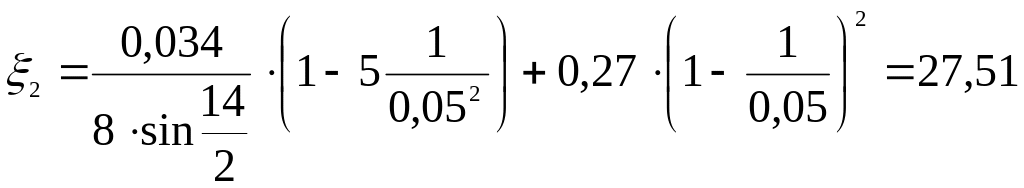 ;
;
![]() .
.
2.3 Расчёт третьего участка – задвижка
Определяем скорость W, на третьем участке из формулы (2.1):
![]() ;
;
где
![]() ,
- плотность жидкости;
,
- плотность жидкости;
;
![]() .
.
Число Рейнольдса Re на третьем участке определяется по формуле(2.2):
![]() ;
;
где , - вязкость жидкости;
;
![]()
Абсолютная шероховатость , м для стальных цельносварных труб определяется из / ист. приложение 2/:
;
Находим
относительную шероховатость
![]() ,
м на третьем участке:
,
м на третьем участке:
![]() ;
;
Определяем режим течения на третьем участке:
![]() ;
;
Сравним
![]() с числом Рейнольдса
с числом Рейнольдса
![]() .
При сравнении получили область
доквадратичного сопротивления.
Коэффициент
рассчитывается по формуле Альтшуля:
.
При сравнении получили область
доквадратичного сопротивления.
Коэффициент
рассчитывается по формуле Альтшуля:
![]() ;
;
![]() ;
;
Определяем потери h, м по длине трубопровода (2.4):
![]() .
.
Вычисли
потери
![]() ,
м на местных сопротивлениях на третьем
участке (2.5):
,
м на местных сопротивлениях на третьем
участке (2.5):
![]() ;
;
![]() ;
;
![]() .
.
2.4 Расчёт суммарных потерь
2.4.1Определение типа трубопровода
Вычислим
суммарные потери по длине трубопровода
![]() ,
м :
,
м :
![]() ;
;
Найдём
суммарные потери на местных сопротивлениях
![]() ,
м :
,
м :
![]() ;
;
Общие
суммарные потери составили
![]() ,м
:
,м
:
![]() ;
;
Так
как
![]() ,
то трубопровод гидравлически короткий.
,
то трубопровод гидравлически короткий.
3 Газодинамический расчёт сопла Лаваля
3.1 Расчёт параметров газа в критическом сечении
Находим
газовую постоянную R,
![]() для азота:
для азота:
![]() ; (3.1)
; (3.1)
Из
уравнения Менделеева-Клайперона находим
плотность газа
,
![]()
![]() при полной остановке:
при полной остановке:
![]() ; (3.2)
; (3.2)
![]() .
.
Находим
скорость звука
![]() ,
,
![]() при полной остановке газа:
при полной остановке газа:
![]() ; (3.3)
; (3.3)
![]() ;
;
где k- показатель адиабаты равный 1,4 для двухатомного газа.
Определим
скорость звука в критическом сечении
![]() ,
:
,
:
![]() ; (3.4)
; (3.4)
![]() ;
;
Максимальную скорость газового потока
![]() ,
находим по формуле:
,
находим по формуле:
![]() ; (3.5)
; (3.5)
![]() ;
;
При расчёте будем пользоваться следующими газодинамическими функциями:
![]() ; (3.6)
; (3.6)
![]() ; (3.7)
; (3.7)
![]() . (3.8)
. (3.8)
В
критическом сечении коэффициент скорости
![]() и число Маха
и число Маха
![]() равны единице:
равны единице:
![]() ;
;
Откуда
находим скорость газового потока в
критическом сечении
![]() ,
:
,
:
![]()
![]() ;
;
Используя
газодинамическую функцию
![]() ,
находим температуру газа
,
находим температуру газа
![]() ,
K
в критическом сечении:
,
K
в критическом сечении:
![]() ;
;
Рассчитаем
давление газа
![]() ,
МПа в критическом сечении, используя
газодинамическую функцию
,
МПа в критическом сечении, используя
газодинамическую функцию
![]() :
:
![]() ;
;
Найдём
плотность газа
![]() ,
в критическом сечении, используя
газодинамическую функцию
,
в критическом сечении, используя
газодинамическую функцию
![]() :
:
![]() ;
;
Из
уравнения неразрывности потока находим
площадь
![]() ,
м2
критического сечения:
,
м2
критического сечения:
![]() ; (3.9)
; (3.9)
![]() ;
;
Находим
диаметр критического
![]() ,
м сечения:
,
м сечения:
![]() ; (3.10)
; (3.10)
![]() .
.
