2.5 Практическая работа №5 Расчёт деревянной стойки

Пример 1 - Проверить прочность и устойчивость деревянной стойки

Исходные данные

Сечение стойки b×h=13×15см.

Продольное усилие N = 200кН

Высота этажа Н = 3,2 м

Материал - дуб 1 сорт.

Класс здания - II.

Сечение ослаблено двумя отверстиями под болты диаметром 16 мм (см. рис.5) верхний конец стойки закреплён шарнирно, нижний - жёстко.

Рисунок 5 - Расчётная схема и сечение стойки

Решение

Расчётное сопротивление древесины сжатию R_с = 15·10³ 1,3 = 19,5 кПа,

где 1,5 – коэффициент т_п для дуба.

Площадь нетто (за вычетом ослаблений)

А_п = b(h - 2d) =0,13(0,15 - 2·0,016 ) = 0,0153м²

Полная площадь (площадь брутто)

A = (b·h) = 0,13·0,15 = 0,0195м²

П роверка прочности по формуле

где γ_n -коэффициент безопасности по назначению, для зданий второго класса γ_n =0,95.

13070 < 20500 кПа

Условие удовлетворяется, прочность стойки обеспечена.

Проверка устойчивости стойки

Расчётная площадь сечения зависит от площади ослаблений и их расположения. Ослабления не выходят на кромку элемента.

Площадь ослаблений сечения отверстиями Ø16

А_осл = 1,6·13·2 = 41,6 см²

Проверим условие

А_осл ≤ 0,25 А

41,6 < 0,25· 195

41,6 < 48,7 см²

Условие удовлетворяется, значит расчётная площадь сечения

А_расч = А = 0,0195м²

Минимальный радиус инерции сечения i_min ,определится

i_min =0,289 b = 0,289·0,13 = 0,0375м.

Расчётная длина элемента

l₀ =μ∙H =0,8∙3,2 = 2,56м,

где μ - коэффициент, зависящий от условий закрепления концов элемента.

Гибкость λ определяется по формуле

λ= l₀ / I_min = 2,56 / 0,0375 = 68,2

При гибкости λ ≤ 70 коэффициент продольного изгиба φ определяется по формуле

φ = 1- а(λ / 100)² , где а = 0,8 для древесины.

φ = 1-0,8(68,2 / 100)² = 0,63

Проверка устойчивости по формуле

20·10³ < 20,5·10³ кПа.

Условие удовлетворяется, устойчивость обеспечена.

Пример 2- Определить несущую способность деревянной стойки из бруса

Исходные данные

Сечение стойки b×h =15×20см

Материал - берёза 2 сорт.

Класс здания I

Высота стойки Н =3,3 м.

Условия закрепления - оба конца шарнирно закреплены (см рис.6 ).

Сечение ослаблено двумя боковыми вырезами по 20 мм.

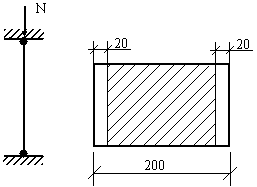
Рисунок 6 - Расчётная схема и сечение стойки

Решение

1. Расчётные характеристики

Расчётное сопротивление древесины R_c = 15·1,1·10³ = 16,5·10³кПа.

Коэффициент надёжности по назначению γ_п = 1.

Площадь нетто А_п , м² определится по формуле

А_п = b(h - 2·a) = 0,15(0,2 - 2·0,02)= 0,024м²

2. Определение несущей способности из условия прочности (см. формулу (8))

N ≤ R_c ∙A_n / γ_n

N ≤ 16,5∙10³∙0,024 / 1 = 396 кН.

2. Определение несущей способности из условия устойчивости

N ≤ φ∙R_c ∙A_расч / γ_n ,

где A_расч - расчётная площадь сечения. Ослабления сечения не выходят на кромку элемента, поэтому принимаем

A_расч = A = 0,15∙0,2 = 0,03 м²

Расчётная длина колонны

l₀ = μ∙l = 1∙2.8 = 2,8 м.

Минимальный радиус инерции сечения

i_min =0,289 b = 0,289·0,15 = 0,043м.

Гибкость λ определяется по формуле

λ= l₀ / i_min = 3,3 / 0,043 = 76,7

При гибкости λ > 70 коэффициент продольного изгиба φ определяется по формуле

φ =В /λ²,

где В = 3000 для древесины.

φ = 3000 / 76,7 =0,51

Несущая способность из условия устойчивости (см. формулу (9)) определяется

N ≤ φ∙R_c ∙A_расч / γ_n ,

N ≤ 0,51∙0,03∙16,5∙10³ / 1 = 252,5кН.

Из двух условий принимаем минимальное значение.

Несущая способность N = 252,5 кН.

Исходные данные к практической работе №5 выдаются по карточкам - заданиям.