
- •Тема 1. Пределы и непрерывность в.1. Предел числовой последовательности
- •В.2. Предел функции
- •В. 3. Бесконечно малые величины
- •В. 4. Бесконечно большие величины
- •В. 5. Основные теоремы о пределах. Признаки существования предела
- •В. 6. Замечательные пределы
- •В.7. Непрерывность функции
- •В.8. Вычисление пределов
- •Тема 2. Дифференциальное исчисление функций одной переменной в.1. Задачи, приводящие к производной. Задача о касательной:
- •В.2. Определение производной функции
- •В.3. Основные правила дифференцирования
- •В.4. Производная сложной и обратной функций
- •В. 5. Производные основных элементарных функций
- •В. 6. Производная степенно-показательной функции
- •В.7. Производные высших порядков
- •В.9. Приложения производной
- •9.1. Правило Лопиталя
- •9.2. Возрастание и убывание функции. Экстремум функции
- •9.3. Исследование функции на выпуклость и точки перегиба
- •9.4. Асимптоты графика функции
- •9.4. Общая схема исследования функций и построения их графиков
- •В.10. Дифференциал функции
- •10.1. Определение дифференциала
- •10.2. Применение дифференциала в приближённых вычислениях
- •10.3. Дифференциалы высших порядков
- •Тема 3. Неопределенный интеграл (ни)
- •1. Первообразная и неопределённый интеграл
- •2. Основные свойства ни:
- •3. Таблица ни
- •4. Методы интегрирования
- •4.1. Метод разложения
- •4.2. Метод замены переменной
- •4.3. Метод интегрирования по частям
- •Тема 4. Определённый интеграл в.1 Формула Ньютона-Лейбница.
- •В.2. Замена переменной и интегрирование по частям в определенном интеграле.
- •Тема 5. Обыкновенные дифференциальные уравнения (оду) в. 1. Основные понятия
- •2.1. Одуi с разделяющимися переменными
- •2.2. Однородные одуi
- •2.3. Линейные одуi
- •3.1. Одуii, допускающие понижение порядка
- •3.2. Линейные одуii с постоянными коэффициентами
В.10. Дифференциал функции
10.1. Определение дифференциала
Пусть функция y = f(x) определена на промежутке Х и дифференцируема в некоторой окрестности точки х Х. Тогда существует конечная производная
![]()
На основании
теоремы о связи бесконечно малых величин
(БМВ) с пределами функций можно записать
![]() ,
где –
,
где –![]() БМВ при x0.
БМВ при x0.
Откуда
![]() .
.
Т.о. приращение функции y состоит из 2 слагаемых: 1) линейного относительно x; 2) нелинейного (которое является БМВ более высокого порядка малости, чем x)
Определение.
Дифференциалом функции называется
главная, линейная относительно x
часть приращения функции, равная
произведению производной данной функции
на приращение независимой переменной ![]() (1)
(1)
Дифференциал независимой переменной равен приращению этой переменной: dx = x
(т.к.
для функции у=х дифференциал будет
равен:
![]() ).
).
Поэтому формулу
(1) можно записать в виде
![]() (2)
(2)
=>
![]() (т.е. производная функции есть отношение
дифференциала функции к дифференциалу
независимой переменной).
(т.е. производная функции есть отношение
дифференциала функции к дифференциалу
независимой переменной).
Пример 9. Найти дифференциал функции у = 6х2 – 3.
Решение.
Вычислим производную данной функции
у = 12х и
подставим в формулу (2):
![]() .
.
Геометрический смысл дифференциала: Дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда х получает приращение x.
На рисунке dy = KN, y = M1N.
dy < y dy > y
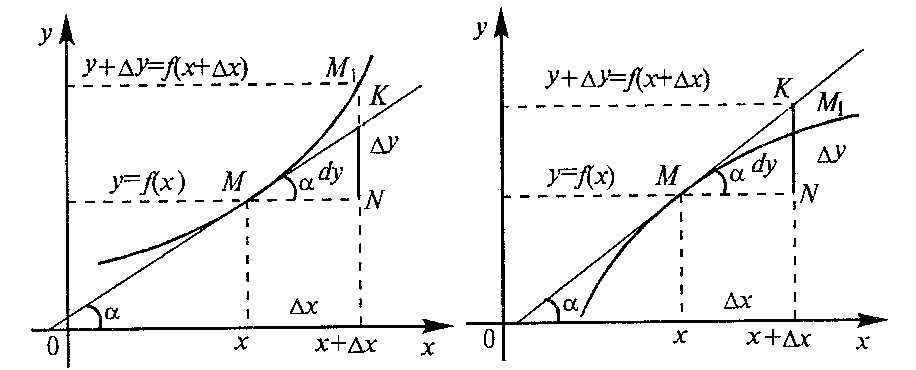
Свойства дифференциала (1-5 аналогичны свойствам производной):
1. dС = 0.
2. d(Сu) = Сdu.
3. d(u v) =du dv.
4. d(uv) = vdu + udv.
5.
![]() .
.
6. Свойство
инвариантности (т.е. неизменности) формы
(формулы) дифференциала. Рассмотрим
сложную функцию
![]() .
.
Тогда
![]() ,
,
т.е. формула дифференциала не изменяется, если вместо функции от независимой переменной х рассматривать функцию от зависимой переменной и.
10.2. Применение дифференциала в приближённых вычислениях
Из изложенного
выше следует, что
.
Поэтому при достаточно малых значениях
x
у
dy или
![]() .
Откуда
.
Откуда
![]() (3)
(3)
Пример 10. Вычислить приближенно, используя дифференциал функции, tg460.
Решение. Для приближенных вычислений воспользуемся формулой (3).
Положим f(x)
= tgx. Найдем
производную f’(x)
= (tgx)’ =
![]() .
Тогда
.
Тогда
![]() .
Учитывая, что tg460
= tg(450
+ 10)
= tg
.
Учитывая, что tg460
= tg(450
+ 10)
= tg![]() ,
возьмем х
=
,
возьмем х
=
![]() и Δх
=
и Δх
=
![]() .
.
Тогда tg460
= tg
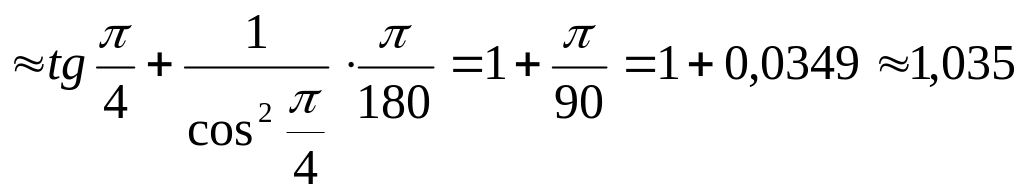 .
.
Пример 11.
Вычислить приближенно
![]() ,
,
Решение . Приближенная формула для вычисления корней n -й степени :
![]() ,
поэтому
,
поэтому
![]()
Возьмем x
=16; x
=0,64 ;![]()
10.3. Дифференциалы высших порядков
Для дифференцируемой
функции y = f(x)
.
Если дифференциал независимой переменной
![]() имеет произвольное, но фиксированное
значение, не зависящее от х, то
имеет произвольное, но фиксированное
значение, не зависящее от х, то
![]() - некоторая функция от х, которая
также может иметь дифференциал.
- некоторая функция от х, которая
также может иметь дифференциал.
Дифференциалом n – го порядка (n – ым дифференциалом) называется дифференциал от дифференциала (n–1)–го порядка данной функции:
![]()
Дифференциал n – го порядка равен произведению производной n – го порядка на n – ю степень дифференциала независимой переменной.
![]() .
(где
.
(где
![]() )
)
=>
![]() .
В отличие от дифференциала первого
порядка дифференциалы более высоких
порядков не обладают свойством
инвариантности формы.
.
В отличие от дифференциала первого
порядка дифференциалы более высоких
порядков не обладают свойством
инвариантности формы.
