Лабораторная работа №… исследование алгоритма арифметического кодирования для сжатия дискретных сообщений

1 Цель работы

1.1 Исследование метода кодирования информации и коэффициента сжатия сообщений.

1.2 Исследование метода декодирования информации.

2 Ключевые положения

В отличие от рассмотренных алгоритмов Шеннона - Фано и Хаффмана, когда кодируемый символ (или группа символов) заменяется соответствующим им кодом, при арифметическом кодировании результат кодирования всего сообщения представляется одним или парой вещественных чисел в интервале от 0 до 1. По мере кодирования исходного текста отображающий его интервал уменьшается, а количество десятичных (или двоичных) разрядов, служащих для его представления, возрастает. Очередные символы входного текста сокращают величину интервала исходя из значений их вероятностей, определяемых моделью. Более вероятные символы делают это в меньшей степени, чем менее вероятные, и, следовательно, добавляют меньше разрядов к результату кодирования.

Алгоритмы Шеннона - Фано и Хаффмана не могут кодировать каждый символ сообщения менее чем 1 битом информации. Предположим, в сообщении, состоящем из 0 и 1, единицы встречаются в 10 раз чаще. Энтропия такого сообщения H(А) ≈ 0,469 (бит/символ). В этом случае желательно иметь метод кодирования, позволяющий кодировать символы сообщения менее чем 1 битом информации. Одним из лучших алгоритмов такого кодирования является арифметическое кодирование.

Арифметическое кодирование использует нестандартный подход к генерации кода. На любом этапе работы арифметического кодирования интервал [0, 1) вещественной прямой делится на интервалы [a, b), каждый из которых соответствует какому-то символу информационного алфавита. Длина интервала численно совпадает с вероятностью появления соответствующего символа на выходе источника информации. Если выбрать любое вещественное число из интервала [0; 1), оно будет принадлежать некоторому интервалу в разбиении, соответствующему вполне определенному символу. Таким образом, число всегда однозначно определяет некоторый символ алфавита.

Пусть в сообщении встретился символ «х», котрому соответствует интервал [a, b), за которым следует символ «y» с соответствующим ему интервалом [c, d). Осуществим равномерную проекцию интервала [0; 1) на интервал [a, b). При такой проекции интервалу [c, d) в интервале [a, b) будет соответствовать интервал [a+(b-a)c, a+(b-a)d). Любое число из последнего интервала однозначно определяет последовательность «хy». Действительно, оно принадлежит интервалу [a, b), который соответствует символу «х», и подинтервалу данного интервала, который обратной проекцией [a, b) на [0; 1) переводится в [c, d). Интервал [c, d) соответствует второму символу последовательности ‑ «y». Процесс построения интервала проиллюстрирован на рис.1.

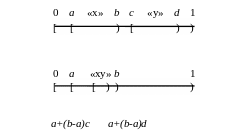
Рисунок 1 – Иллюстрация работы арифметического кодирования

2.1 Кодирование

Поясним идею арифметического кодирования на примере. Пусть нам нужно закодировать следующую текстовую строку: МАТЕМАТИКА

Перед началом работы кодера соответствующий кодируемому тексту исходный интервал составляет [0; 1).

Алфавит кодируемого сообщения содержит следующие символы: {М, А, Т, Е, И, К}.

Определим количество (встречаемость, вероятность) каждого из символов алфавита в сообщении и назначим каждому из них интервал, пропорциональный его вероятности. С учетом того, что в кодируемом слове всего 10 букв, получим табл. 1.

Таблица 1

Символ	Вероятность	Интервал
М	0,2	[0; 0,2)
А	0,3	[0,2; 0,5)
Т	0,2	[0,5; 0,7)
Е	0,1	[0,7; 0,8)
И	0,1	[0,8; 0,9)
К	0,1	[0,9; 1,0)

Располагать символы в таблице можно в любом порядке: по мере их появления в тексте, в алфавитном или по возрастанию вероятностей – это не принципиально. Результат кодирования при этом будет разным, но эффект – одинаковым.

После просмотра первого символа сообщения «М» кодер сужает исходный интервал [0; 1) до нового [0; 0,2). Таким образом, после кодирования первой буквы результат кодирования будет находиться в интервале [0; 0,2).

Следующий символ «А» кодируется подинтервалом внутри интервала, выделенного для предыдущих символов, сужая его до [0,04; 0,1) - верхняя и нижняя границы нового интервала определяются как начало предыдущего интервала плюс произведение ширины этого интервала на значения границ отрезка, отвечающего текущему символу (табл. 1): (нижняя = 0+0,20,2 = =0,04; верхняя = 0+0,50,2 = 0,1).

Следующий символ, поступающий на вход кодера, – это буква «Т» (символу «Т» соответствует отрезок [0,5; 0,7) в таблице кодера (табл. 1)). Применительно к уже имеющемуся рабочему интервалу сообщения, состоящего из предыдущих букв, новый интервал будет [0,07; 0,082) (нижняя = 0,04+0,60,5 = 0,07; верхняя = 0,04+0,60,7 = 0,082) и т. д.

Таким образом, последовательность интервалов, соответствующих кодируемому сообщению, будет следующей (табл. 2):

Таблица 2

Символ – интервал	Интервал сообщения	Ширина интервала
М - [0; 0,2)	[0; 0,2)	0,2
А - [0,2; 0,5)	[0,04; 0,1)	0,6
Т - [0,5; 0,7)	[0,07; 0,082)	0,012
Е - [0,7; 0,8)	[0,0784; 0,0796)	0,0012
M - [0; 0,2)	[0,0784; 0,07864)	0,00024
А - [0,2; 0,5)	[0,078448; 0,07852)	0,7210-4
Т - [0,5; 0,7)	[0,078484; 0,0784984)	0,14410-4
И - [0,8; 0,9)	[0,07849552; 0,07849696)	0,14410-5
К - [0,9; 1,0)	[0,078496816; 0,07849696)	0,14410-6
А - [0,2; 0,5)	[0,0784968448; 0,078496888)	0,43210-7

Результат кодирования сообщения МАТЕМАТИКА - это вещественное число, принадлежащее интервалу [0,0784968448; 0,078496888). Целое число, принадлежащее данному отрезку, деленное на минимальную степень 2, - это 0,07849687 = 1316959/2²⁴. Двоичный 24-разрядный код числа 1316259₁₀=000101000001100001011111₂. Этот код и будет арифметическим кодом сообщения – МАТЕМАТИКА = 000101000001100001011111.

Коэффициент сжатия:

(4)

где N_вх – количество двоичных символов, используемых для представления сообщения на входе кодера;

N_вых – количество двоичных символов, используемых для представления сообщения на выходе кодера.

При использовании равномерного (примитивного) кода с объемом алфавита М_А = 6 букв, n = 3, N_вх = 3 × 10 = 30 бит, N_вых = 24 бита, коэффициент сжатия η = 30/24 = 1,25.

Принципиальное отличие арифметического кодирования от методов сжатия Шеннона-Фано и Хаффмана в его непрерывности, т.е. в отсутствии необходимости блокирования сообщения. Эффективность арифметического кодирования растёт с ростом длины сжимаемого сообщения, однако требует больших вычислительных ресурсов.

2.2 Декодирование

Предположим, что декодер знает о тексте конечный интервал [0,0784968448; 0,078496888)

Декодеру, как и кодеру, известна также таблица распределения выделенных алфавиту интервалов. Он определяет, что первый закодированный символ это М, так как результат кодирования целиком лежит в интервале [0; 0,2), выделенном моделью символу М согласно таблице 1.

Повтоpим действия кодера:

вначале [0; 1);

после пpосмотpа [0; 0,2).

Исключим из результата кодирования влияние теперь уже известного первого символа М, для этого вычтем из результата кодирования нижнюю границу диапазона, отведенного для М, – 0,0784968448 – 0 = 0,0784968448 – и разделим полученный результат на ширину интервала, отведенного для М, – 0,2. В результате получим 0,0784968448 / 0,2 = 0,392484224. Это число целиком вмещается в интервал, отведенный для буквы А, – [0,2; 0,5), следовательно, вторым символом декодированной последовательности будет А.

Поскольку теперь мы знаем уже две декодированные буквы - МА, исключим из итогового интервала влияние буквы А. Для этого вычтем из остатка 0,392484224 нижнюю границу для буквы А 0,392484224 – 0,2 = =0,192484224 и разделим результат на ширину интервала, отведенного для буквы А, то есть на 0,3. В результате получим 0,192484224 / 0,3=0,64161408. Результат лежит в диапазоне, отведенном для буквы Т, следовательно, очередная буква будет Т.

Исключим из результата кодирования влияние буквы Т. Получим (0,64161408 – 0,5)/0,2 = 0,7080704. Результат попадает в интервал, отведенный для буквы Е, следовательно, очередной декодированный символ – Е, и так далее, пока не декодируем все символы (табл. 3).

Таблица 3

Декодируемое число	Символ на выходе	Границы		Ширина интервала
		нижняя	верхняя
0,0784968448	М	0	0,2	0,2
0,392484224	А	0,2	0,5	0,3
0,64161408	Т	0,5	0,7	0,2
0,7080704	Е	0,7	0,8	0,1
0,080704	М	0	0,2	0,2
0,40352	А	0,2	0,5	0,3
0,6784	Т	0,5	0,7	0,2
0,892	И	0,8	0,9	0,1
0,92	К	0,9	1	0,1
0,2	А	0,2	0,5	0,3
0	Конец декодирования