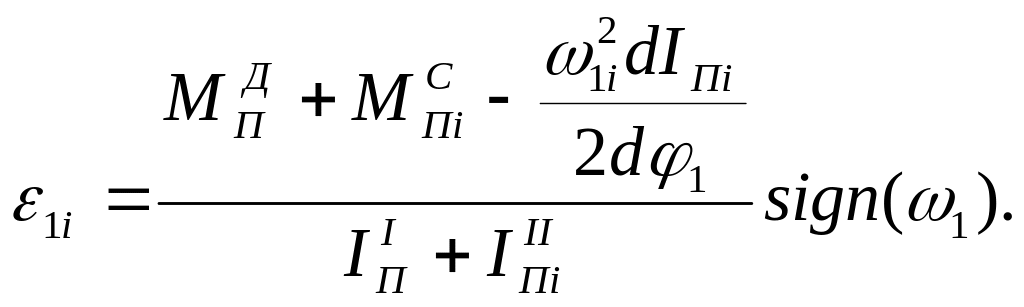3.6.1 Определение приведённых моментов сил сопротивления и движущихся сил.

Определение выполняется из условия равенства мгновенных скоростей:

Откуда:

- проекции силы на оси координат;

- проекции аналога скорости точки приложения силы ;

- передаточная функция от i-го звена, к которому приложен момент , к звену 1;

=-1 при направлении вращения звена по часовой стрелке.

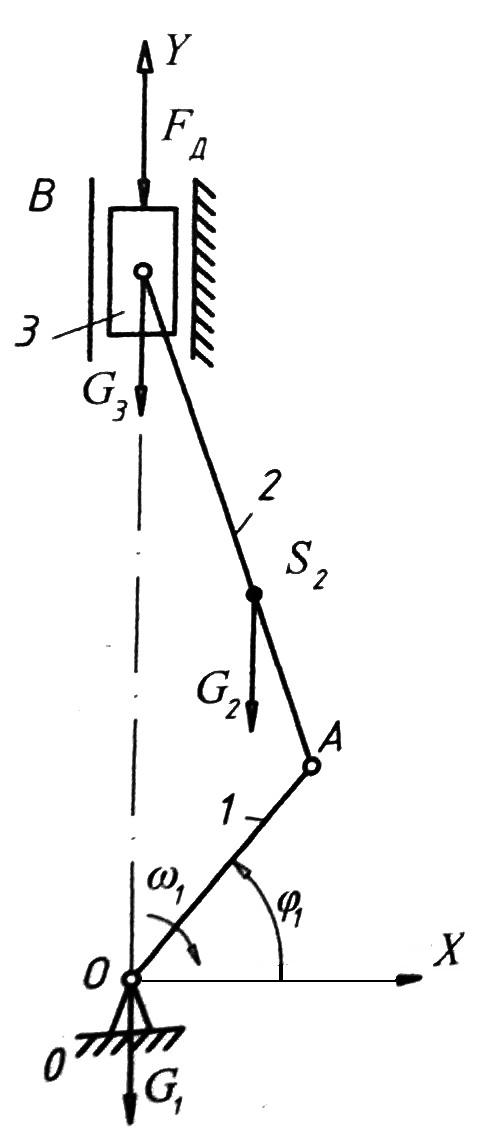
Для вертикального механизма получаем:

Сила отрицательна, т.к. она направлена против положительного направления оси OY.

Для второго положения:

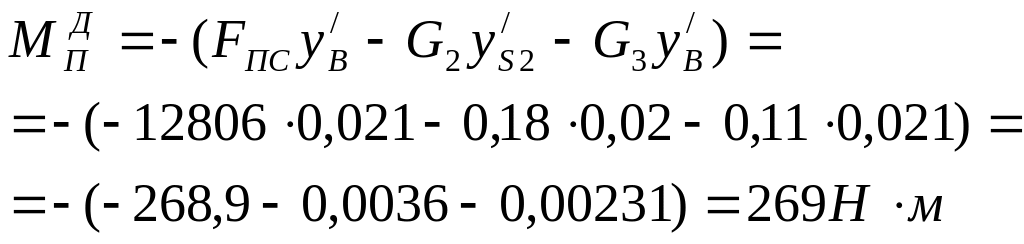
Приведённый момент движущих сил определяется из условия, что при установившемся режиме движения изменение кинетической энергии машины за цикл равно нулю, т.е. , откуда за цикл

Работа сил сопротивления вычисляется по формуле:

Интегрирование выполняется численным методом по правилу трапеций:

, где - шаг интегрирования в радианах.

.

С учётом при

3.6.2 Определение переменной составляющей приведённого момента инерции.

Переменная составляющая определяется из условия равенства кинетических энергий, т.е. кинетическая энергия звена приведения, имеющая момент инерции , равна сумме кинетических энергий звеньев, характеризуемых переменными передаточными функциями:

Разделив это выражение на , с учётом того что , получим:

Для звеньев 2,3 кривошипно-ползунного механизма:

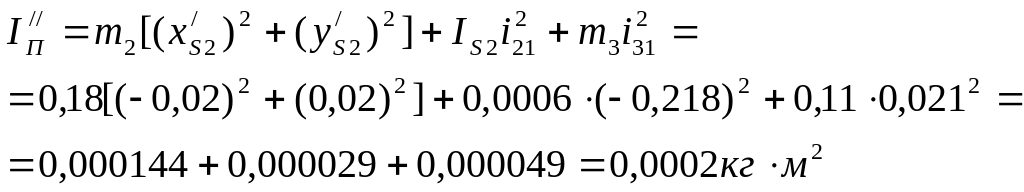
Производная , необходимая в последующем для определения закона движения звена приведения, имеет вид:

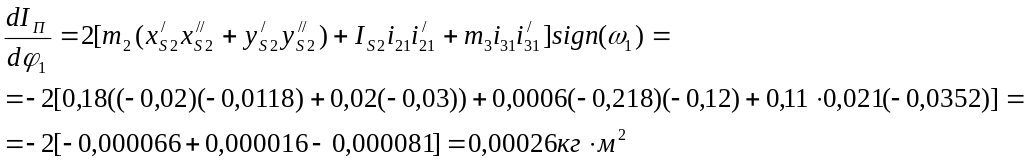
3.6.3 Определение постоянной составляющей приведённого момента инерции и момента инерции маховика.

В основу расчёта положен метод Н.И. Мерцалова. Для определения изменения кинетической энергии машины предварительно определяем работу движущих сил . Для i-го положения:

, где .

Тогда .

Изменение кинетической энергии звеньев с постоянным приведённым моментом инерции равно:

, где - кинетическая энергия звеньев, создающих переменную составляющую По методу Н.И. Мерцалова определяется приближенно по средней угловой скорости :

Далее из полученного за цикл массива значений находим максимальную и минимальную величины, используя которые вычисляем максимальный перепад кинетической энергии:

.

Тогда необходимая величина , при которой имеет место вращение звена приведения с заданным коэффициентом неравномерности , равна:

, где

Момент инерции маховика определяется по формуле:

, где - приведённый момент инерции всех вращающихся масс машины (ротора двигателя, зубчатых колёс, кривошипа). - задано в условии курсового проекта.

Иногда величина может оказаться больше полученного значения . Это означает, что не требуется установка маховика.

.

3.6.4 Определение законов движения звена приведения.

С помощью зависимости , используемой при определении постоянной составляющей приведённого момента инерции по методу Мерцалова, можно получить зависимость угловой скорости звена приведения .

Для любого положения кинетическая энергия звеньев, обладающих постоянным приведённым моментом инерции , равна:

, где

Так как то текущее значение угловой скорости:

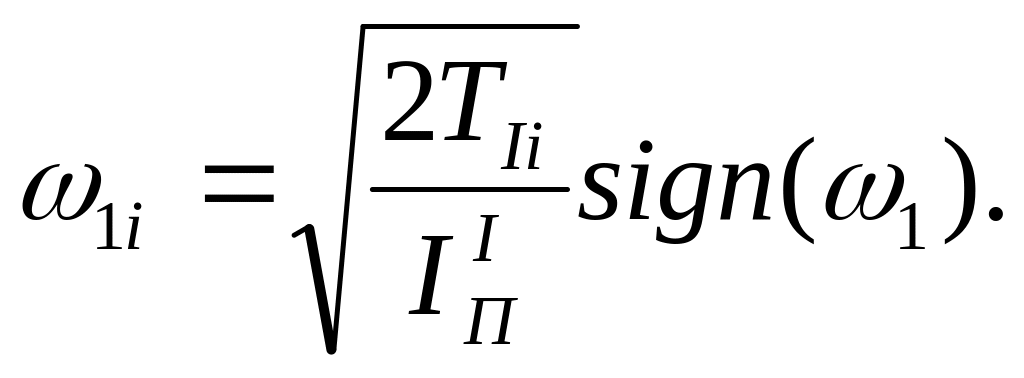
Угловое ускорение определяется из дифференциального уравнения движения звена приведения: