4.1.4 Аналитическое определение скоростей и точек звеньев механизма

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

4.2 Определение сил, действующих на звенья механизма

Определение сил тяжести:

а) для кривошипа:

;

б) для шатуна:

в) для ползуна:

Движущая сила:

Силы инерции:

а) для кривошипа:

б) для шатуна:

в) для ползуна:

Моменты инерции:

1. для кривошипа:

б) для шатуна:

в) для ползуна:

(ε = 0).

4.3 Силовой расчёт механизма (методом кинетостатики)

Для построения плана положения выбираем масштабный . Строим план положения и прикладываем силы, действующие на звенья 2 и 3. Реакцию во вращательной паре А представляем в виде двух составляющих: нормальная – и тангенциальная – .

К шатуну в точке прикладываем силу тяжести G₂ и силу инерции F₁₂. Силу инерции направляем параллельно a_S2 на плане ускорений в противоположную сторону. Момент инерции Ми₂ направлен противоположно угловому ускорению ( расстояния от линии действия сил G₂ и _F12 до точки В соответственно).

Приложим силы, действующие на ползун 3: силу тяжести G₃, силу инерции Fи₃, движущую силу F₃, реакцию F_3O , действующую на ползун со стороны стойки.

4.3.1 Построение плана положений группы Ассура (2;3) и определение динамических реакций в кинематических парах

Для построения плана положения выбираем масштабный коэффициент длины м/мм.

Составим векторное уравнение равновесия группы Асура (2;3):

Определим тангенциальную составляющую , для чего составим уравнение суммы моментов, относительно точки С:

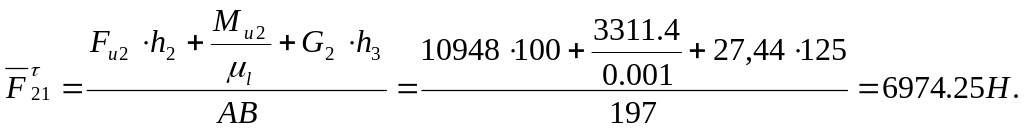
Выбираем масштабный коэффициент , после чего найдём длины векторов на плане сил:

[1–2] =

[2–3] =

[3–4] =

[4–5] =

[5–6] =

[6–7] =

Построение плана сил осуществляется следующим образом:

На чертеже произвольно выбираем точку 1, из которой проводим вектор [1–2] перпендикулярно АВ и вследствие чего получаем точку 2. Из точки 2 проводим вектор [2–3] параллельно F_и2. Затем [3–4] || G₂, [4–5] || G₃, [5–6] - || F _и3 [6–7] - || F ₃. После чего из точки 7 проводим прямую, которая параллельна линии действия реакции F_3O. Из точки 1 проводим прямую, которая параллельна линии действия реакции Fⁿ₂₁. В результате пересечения этих прямых получаем точку 8. Тогда вектор [7–8] соответствует реакции R₃₀, a вектор [8–1] соответствует реакции Fⁿ₂₁. Соединив точки 8 и 2 и получаем полную реакцию F_21.

Реакции и неизвестны по величине, но известны по направлению. Измерим векторы неизвестных реакций и полученные значения умножим на масштабный коэффициент силы.

=[8–1]

=[8–2]

=[7– 8]

Соединяем точки 4 и 8, в результате чего получаем на чертеже вектор реакции . Для того чтобы узнать величину этого вектора, необходимо измерить длину вектора и умножить её на масштабный коэффициент длины:

=[4–8]

4.3.3 Построение плана положения механизма 1 класса

Выделяем кривошип из механизма и вычерчиваем его в масштабе м/мм.

Прикладываем силы, действующие на звено 1 – кривошип. В точке А действует реакция со стороны отброшенного звена 2. В точке О прикладываем силу тяжести и реакцию , действующую со стороны стойки. Противоположно направлению углового ускорения прикладываем главный момент инерции и уравновешивающий момент M_y. ( — расстояние от точки О до линии действия реакции ).