- •Киевская государственная академия водного транспорта
- •Курсовая работа
- •Глава 1. Штурманское описание выбранного участка судоходного пути.
- •Глава 2. Маневрирование судном на выбранном участке судоходного пути.
- •Глава 3. Обеспечение безопасности плавания и охрана окружающей среды на выбранном участке судового пути.
- •Глава 1. Штурманское описание выбранного участка судоходного пути.
- •1.1. Навигационно-гидрографическое описание выбранного участка судоходного пути. Общие сведения
- •Затоплені поселення
- •Порты, пристани, убежища
- •Путевая и гидрометеорологическая информация
- •1.2 Гидрометеорологические условия плавания на выбранном участке судоходного пути. Ветровой режим.
- •Волнение.
- •Туманы.
- •Колебания уровня воды
- •1.3 Штурманское описание выбранного участка судоходного пути.
- •Глава 2. Маневрирование судном на выбранном участке судоходного пути.
- •2.1 Маневрирование судном при движении на прямолинейных и искривленных участках судоходного пути.
- •2.2. Принцип маневрирования судном при прохождении перевалов и перекатов по и против течения.
- •2.3 Решение маневренной задачи по заданию преподавателя.
- •Глава 3. Обеспечение безопасности плавания и охрана окружающей среды на выбранном участке судового пути.
- •Общий порядок движения судов на выбранном участке судоходного пути при нормальной видимости.
- •3.2 Общий порядок движения судов на выбранном участке судоходного пути при ограниченной видимости.
- •3.3. Правила обгона и расхождения судов.
- •3.4. Применение правил плавания на выбранном «сложном» участке судоходного пути в условиях нормальной и ограниченной видимости.
- •6.20 Составы судов
- •6.21 Плавание вблизи плавучих средств, выполняющих работы, и судов, севших на мель или затонули, а также судов, лишенных в возможности управляться
- •3.5. Действие в аварийных ситуациях и предотвращение загрязнения окружающей среды с судов.
- •Список использованной литературы.
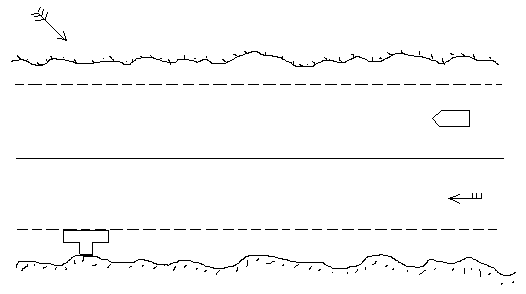
2.3 Решение маневренной задачи по заданию преподавателя.
![]()
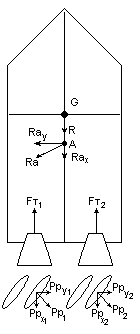
1. 1.1. Σ Fx = Fт1 + Fт2 – R – Rax V = const, следовательно Fт1 + Fт2 – R – Rax = 0
Вывод: судно движется на переднем ходу с постоянной скоростью
1.2.Σ Fу = Fт1 + Fт2 – Ra Вывод: судно начинает смещаться влево Fт1 + Fт2 – Ra = 0
Fт1l1 – Fт2l2 – Ppyl3 – Ppyl4
1.3.Σ М = Fт1* l1 - Fт2* l1 – Pp1у* l2 – Pp2у * l2 + Raу * l3 = – 2Fт1у* l2 + Raу * l3
Если: Fт1 = Fт2 Ppy1 = Ppy2
– 2Fт* l1 – Ra + 2Ppy
|
ветер
течение |
Вывод: судно начнет вращаться против часовой стрелки
Общий вывод: судно движется прямолинейно с постоянной скоростью
2.
Fт1 =Fт2; Fт1x + Fт2x < 1.Fт1 + Fт2 => Σ Fx = ΔΣ – R (Σ R = – R – Rax)
Вывод: т.к суммарная сила со знаком „-”, судно будет тормозить
2.2. Σ Fу = Fт1 + Fт2 +Rтy – Ray Fт1у = Fт2у 2Fт1у +Rтy > Ray
Вывод: поскольку по оси «у» преобладают силы со знаком «+», корма судна будет смещаться вправо
2.3. Σ М = Fт1* l1 - Fт2* l1 – Pp1у* l2 – – Pp2у * l2 + Raу * l3 = – 2Pp1у* l3 + Raу * l3
Если: Fт1x = Fт2x l1 Pp1у = Pp2у l2
– 2Fт1у* l2 > Raу * l3
Вывод: т.к. преобладают моменты со знаком «-», судно будет вращаться против часовой стрелки
|
ветер
течение
|
3. 3.1 Σ Fx = Fт1 + Fт2 + Rт – R – Rax Fт1 =Fт2; Fт1 + Fт2 < 2. Fт1 + Fт2 => Σ Fx = ΔΣ – R (Σ R = – R – Rax)
Вывод: т.к суммарная сила со знаком „-”, судно будет тормозить
3.2. Σ Fу = – Fт1у - Fт2у +Rтy – Ray - Рр1у = – Рр2у -2Рр1у +Rтy > Ray
Вывод: поскольку по оси «у» преобладают силы со знаком «-», корма судна будет смещаться влево
3.3. Σ М = Fт1* l1 - Fт2*l1 + Рр1у*l2 + Рр2у * l2 + Raу * l3 = 2Рр1у* l2 + Raу * l3
Если: Fт1 = Fт2 l1 Рр1у = Рр2у l2
Σ М = 2Рр1у* l2 + Raу * l3
Вывод: корпус будет вращаться по часовой стрелке |
ветер
течение |
Приложения 1.
Графическое представления расстановки сил в заданный момент маневрирования указано в пункте 2.3.

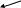
 2
2 .1.
Σ Fx
= Fт1
+ Fт2
+ Rт
– R
– Rax
.1.
Σ Fx
= Fт1
+ Fт2
+ Rт
– R
– Rax