12. Графічний метод для задач лп

n-вимірного простору при .

Нехай кількість змінних n

число обмежень m,

.

Дві з n змінних, наприклад х₁ та х₂ вільні, інші m базисні

рівнянь вигляду:

Оскільки , то

,

(2.19.1)

Узявши величину х₃ рівною нулю, отримаємо рівняння:

.

Для такої прямої ,

Відмітимо ту півплощину , де . Аналогічно ; ;...; . Спільна частина площини в - багатокутник допустимих розв’язків.

Необхідно знайти максимальне значення функціонала:

.

Підставивши , , , ...; з (2.19.1) у функціонал, отримаємо F через дві вільні змінні та :

,

де — вільний член. Далі відшукання оптимального плану здійснюється за алгоритмом для випадку двох змінних.

Р озв’язати графічним методом задачу лінійного програмування

.

Розв’язання.

n = 7 — кількість змінних, m = 5 — кількість обмежень.

вільні змінні х₁ та х₂ і виразимо через них всі базисні змінні.

(2.19.2)

, (2.19.3)

. (2.19.4)

;

.

Далі за алгоритмом беремо х₁ = 0 та х₂ = 0 — координатні осі; інші обмежуючі прямі знаходимо, узявши х₃ = 0, х₄ = 0, х₅ = 0, х₆ = 0, х₇ = 0. Багатокутник допустимих розв’язків зображено на рис. 2.12.

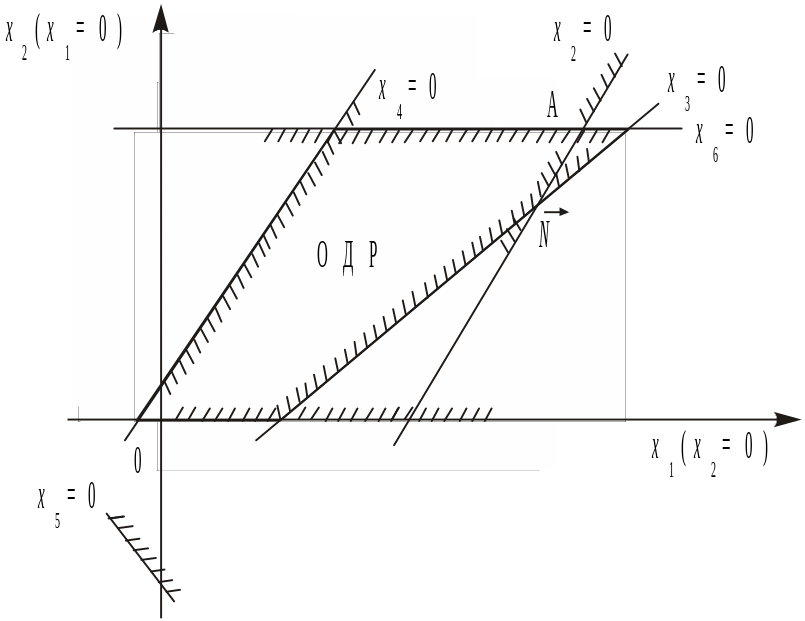
Рис. 2.12

Знайдемо вигляд функціонала, вираженого через х₁ та х₂.

.

Відкидаючи вільний член, маємо: .

Будуємо вектор (–5, –2), а перпендикулярно пряму F^'.

Рухаючи пряму F^' в напрямку, протилежному (необхідно знайти мінімальне значення функції F), отримаємо точку мінімуму — А (рис. 2.13).

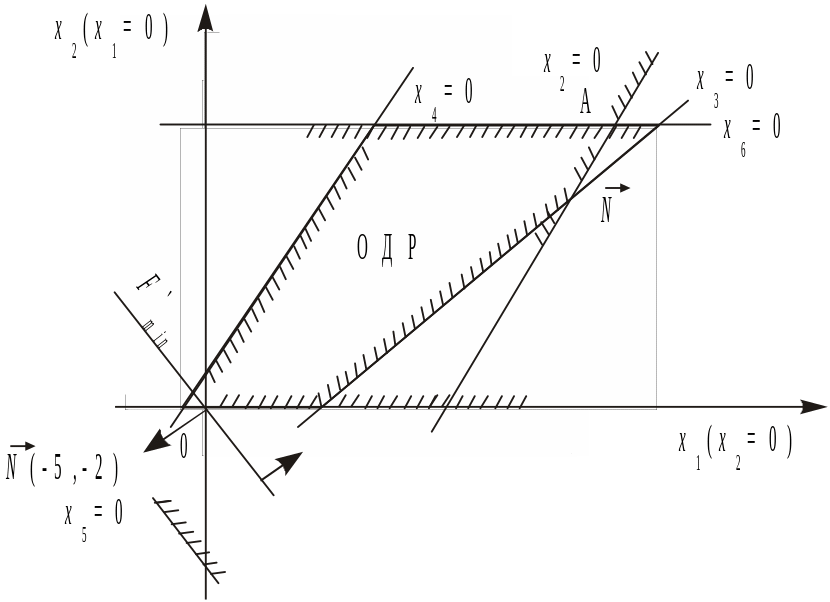
Рис. 2.13

У точці А перетинаються дві обмежуючі прямі: х₆ = 0 та х₇ = 0.

= 8,5; = 5.

Звідки

= 0,5; = 16,5; = 17,5; = 0; = 0.

Підстановкою значень та в лінійну функцію F отримуємо значення цільової функції:

.

Симплексний метод розв’язування задач лінійного програмування

З властивостей розв’язків задачі лінійного програмування відомо: оптимальний розв’язок задачі має знаходитись в одній з кутових точок багатогранника допустимих розв’язків. Загальна кількість опорних планів визначається кількістю комбінацій .

1949 року американським вченим Дж. Данцігом запропоновано симплекс-метод.

13. Початковий опорний план

Розглянемо задачу лінійного програмування, записану в канонічній формі:

.

Не порушуючи загальності, допустимо, що система рівнянь містить перші m одиничних векторів. Отримаємо:

(2.36)

(2.37)

(2.38)

Система обмежень (2.37) у векторній формі матиме вигляд:

, (2.39)

де

, ,..., ,

, …, , ,

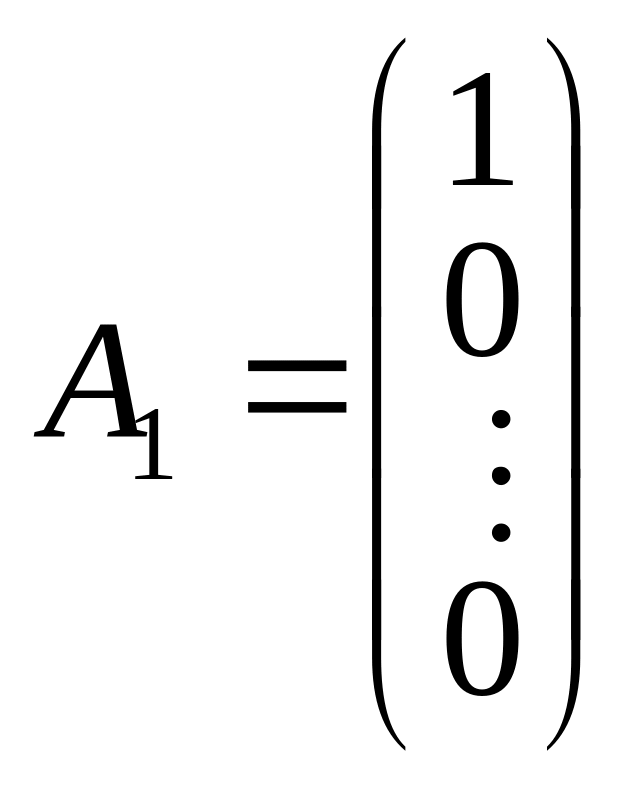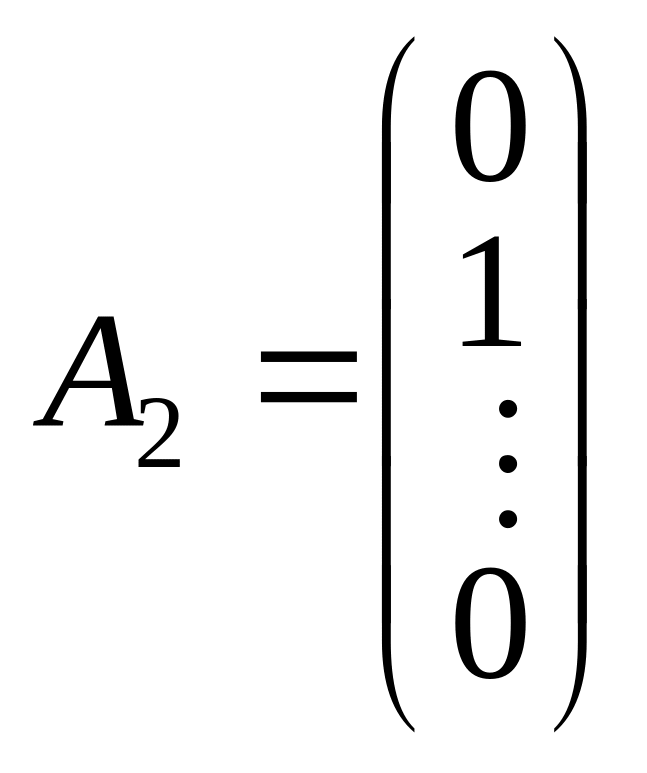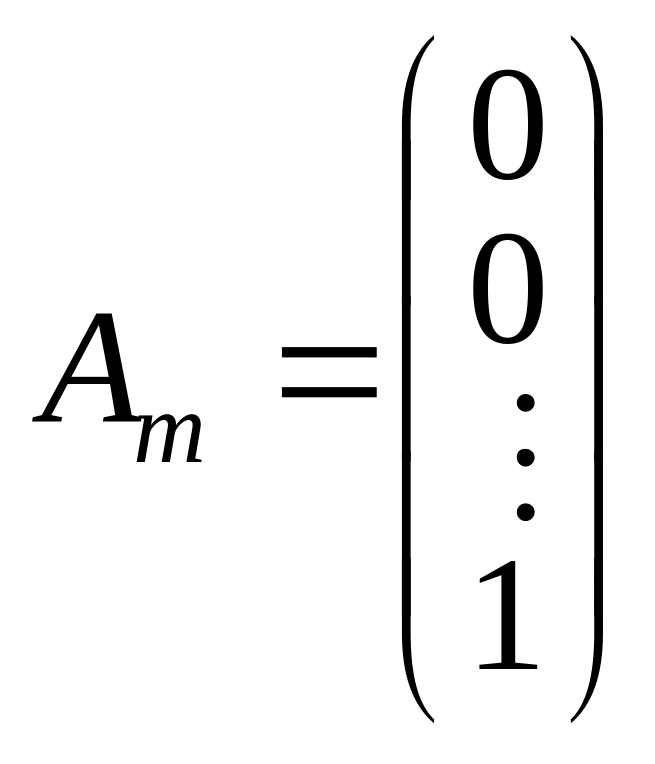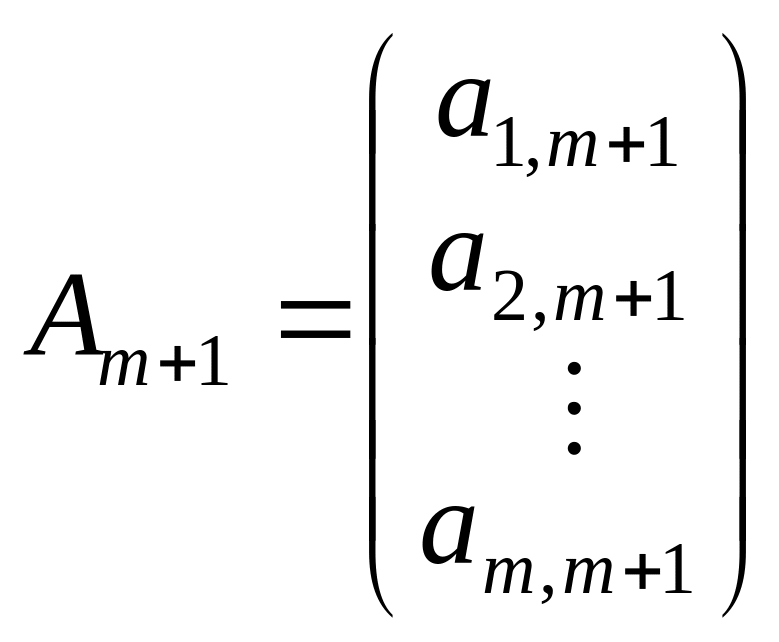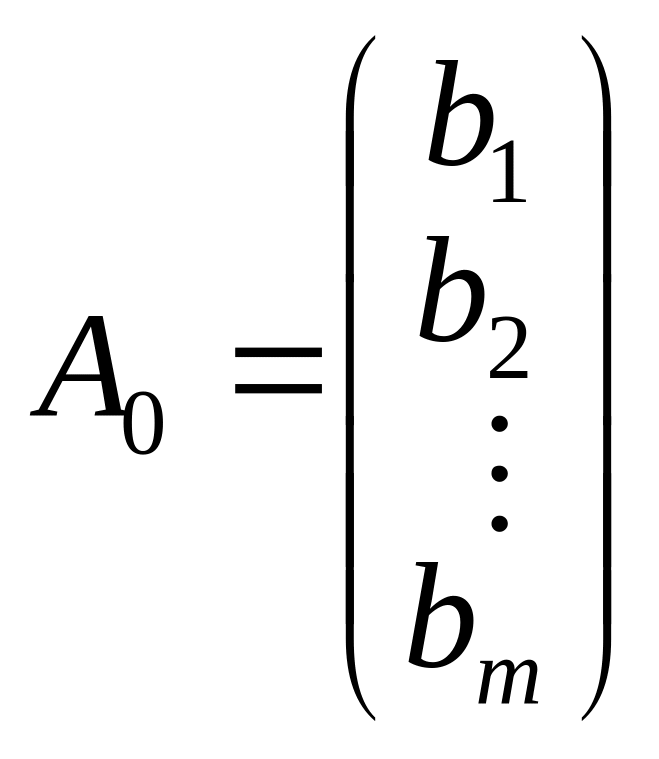— лінійно незалежні одиничні вектори m-вимірного простору, що утворюють одиничну матрицю і становлять базис цього простору.

Тому в розкладі (2.39) базисними змінними будуть , а інші змінні — вільні.

Прирівняємо всі вільні змінні до нуля,

.

Оскільки , а вектори — одиничні, то отримаємо один із розв’язків системи обмежень (2.37):

(2.40)

тобто допустимий план.

Такому плану відповідає розклад

(2.41)

де — лінійно незалежні вектори і за властивістю 3 розв’язків задачі лінійного програмування план є кутовою точкою багатогранника розв’язків, а отже, може бути почат­ковим опорним планом.